TOP 15 câu Trắc nghiệm Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm (Cánh diều 2024) có đáp án - Toán 10
Bộ 15 câu hỏi trắc nghiệm Toán lớp 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 3.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Cánh diều bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm - Cánh diều
Câu 1. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh thành ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
Hãy tính khoảng biến thiên của mẫu số liệu trên.
A. 40;
B. 20;
C. 61;
D. 1.
Đáp án đúng là: B
Theo bảng số liệu trên ta có: Giá trị lớn nhất của số liệu là 45; giá trị nhỏ nhất của số liệu là 25.
Khoảng biến thiên : R = 45 – 25 = 20.
Câu 2. Tìm khoảng tứ phân vị của mẫu số liệu sau:
200 240 220 210 225 235 225 270 250 280.
A. 80;
B. 20;
C. 30;
D. 10.
Đáp án đúng là: C
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:
200 210 220 225 225 235 240 250 270 280
Trung vị của mẫu số liệu trên là: = 230 ⇒ Q2 = 230
Nửa dãy phía dưới số 230 (nghĩa là những số nhỏ hơn 230) gồm: 200 210 220 225 225 có trung vị là 220 ⇒ Q1 = 220
Nửa dãy phía trên số 230 ( nghĩa là những số lớn hơn 230) gồm: 235 240 250 270 280 có trung vị là 250 ⇒ Q3 = 250
Do đó, tứ phân vị của mẫu số liệu: Q1 = 220; Q2 = 230; Q3 = 250
Vậy khoảng tứ phân vị của mẫu số liệu là: ∆Q = Q3 – Q1 = 250 – 220 = 30.
Câu 3. Tiến hành đo huyết áp của 8 người ta thu được kết quả sau:
77 105 117 84 96 72 105 124
Hãy tìm khoảng tứ phân vị của mẫu số liệu trên.
A. 10;
B. 20;
C. 10,5;
D. 30,5.
Đáp án đúng là: D
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:
72 77 84 96 105 105 117 124
Trung vị của mẫu số liệu trên là: = 100,5 ⇒ Q2 = 100,5
Nửa dãy phía dưới số 100,5 ( nghĩa là những số nhỏ hơn 100,5) gồm: 72 77 84 96 có trung vị là = 80,5 ⇒ Q1 = 80,5
Nửa dãy phía trên số 100,5 ( nghĩa là những số lớn hơn 100,5) gồm: 105 105 117 124 có trung vị là =111 ⇒ Q3 = 111
Do đó, tứ phân vị của mẫu số liệu: Q1 = 80,5 ; Q2 = 100,5; Q3 = 111
Vậy khoảng tứ phân vị của mẫu số liệu là: ∆Q = Q3 - Q1 = 111 – 80,5 = 30,5
Câu 4. Điều tra về số học sinh của một trường THPT như sau:
|
Khối lớp |
10 |
11 |
12 |
|
Số học sinh |
1120 |
1075 |
900 |
Khoảng biến thiên của mẫu số liệu trên là.
A. 220;
B. 45;
C. 175;
D. 3095.
Đáp án đúng là: A
Giá trị lớn nhất của mẫu số liệu là 1120 và giá trị nhỏ nhất của mẫu số liệu là 900.
Vậy khoảng biến thiên: R = 1120 – 900 = 220.
Câu 5. Nếu đơn vị của số liệu là hm thì đơn vị của phương sai là
A. m2;
B. ha;
C. m3;
D. hm.
Đáp án đúng là: B
Nếu đơn vị của số liệu là hm thì đơn vị của phương sai là hm2
Mà 1 hm2 = 1 ha
Câu 6. Chọn khẳng định sai trong các khẳng định sau:
A. Phương sai luôn là một số không âm;
B. Phương sai là bình phương của độ lệch chuẩn;
C. Phương sai càng lớn thì độ phân tán so với số trung bình cộng càng lớn;
D. Phương sai luôn lớn hơn độ lệch chuẩn.
Đáp án đúng là: D
Phương sai là s2 và độ lệch chuẩn s = nhưng không thể khẳng định phương sai lớn hơn độ lệch chuẩn
Câu 7. Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây?
A. Số trung bình;
B. Số trung vị;
C. Mốt;
D. Phương sai.
Đáp án đúng là: D
Dựa vào ý nghĩa của phương sai và độ lệch chuẩn để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình.
Câu 8. Phương sai của dãy số 2; 3; 4; 5; 6; 7 là.
A. 4.5;
B. 3,1;
C. 2,92;
D. 2.
Đáp án đúng là: C
Ta có: = 4,5
⇒ s2 = ≈2,92.
Câu 9. Sản lượng vải thiều (tạ) thụ hoạch được của 20 hộ gia đình trong một hợp tác xa được ghi ở bảng sau:
|
15 |
13 |
15 |
12 |
13 |
12 |
15 |
15 |
14 |
14 |
|
14 |
18 |
17 |
12 |
12 |
14 |
16 |
14 |
18 |
15 |
Tìm phương sai s2?
A. 3,4;
B. 1,84;
C. 1,8;
D. 3,24.
Đáp án đúng là: D
Từ bảng số liệu trên ta suy ra được bảng phân bố tần số như sau:
|
Sản lượng (tạ) |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
Số hộ gia đình |
4 |
2 |
5 |
5 |
1 |
1 |
2 |
Sản lượng vải trung bình là: = 14,4 (tạ)
Phương sai s2 là:
s2 == 3,24
Câu 10. Độ lệch chuẩn là:
A. Bình phương của phương sai;
B. Một nửa của phương sai;
C. Căn bậc hai của phương sai;
D. Nghịch đảo của phương sai.
Đáp án đúng là: C
Căn bậc hai của phương sai được gọi là độ lệch chuẩn.
Câu 11. Theo thống kê điểm thi giữa kì 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là s2 = 0,573. Độ lệch chuẩn của bảng thống kê đó bằng:
A. 0,182;
B. 0,757;
C. 0,936;
D. 0,657.
Đáp án đúng là: B
Ta có công thức tính độ lệch chuẩn là s = = ≈0,757.
Câu 12. Thời gian chạy 50 m của 20 học sinh được ghi lại trong bảng sau đây:
|
Thời gian (giây) |
8,3 |
8,4 |
8,5 |
8,7 |
8,8 |
|
Tần số |
2 |
3 |
9 |
5 |
1 |
Hãy tìm độ lệch chuẩn của mẫu số liệu đã cho.
A. 0,14;
B. 0,0191;
C. 8,53;
D. 8,5.
Đáp án đúng là: A
Ta có: = = 8, 53
Phương sai là: s2 =
= 0,0191
⇒ s = 0,14.
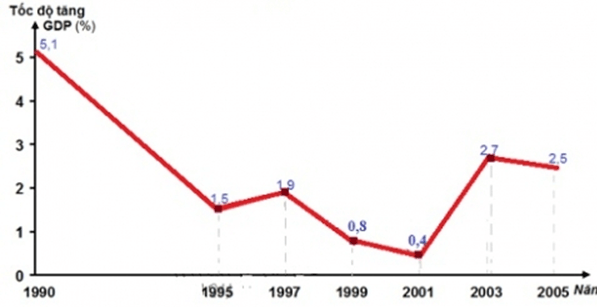
Câu 13. Biểu đồ sau biểu diễn tốc độ tăng trưởng GDP của Nhật Bản trong giai đoạn 1990 đến 2005. Hãy tìm khoảng biến thiên của mẫu số liệu đó.
A. 5,1;
B. 5,5;
C. 0,4;
D. 4,7.
Đáp án đúng là: D
Ta có giá trị lớn nhất của mẫu số liệu là 5,1 và giá trị nhỏ nhất của mẫu số liệu là 0,4
⇒ R = 5,1 – 0,4 = 4,7.
Câu 14. Cho mẫu số liệu: 10 7 8 5 4. Tính độ lệch chuẩn của mẫu số liệu đó.
A. 6,8;
B. 2,14;
C. 4,56;
D. 20,79.
Đáp án đúng là: B
Ta có: = = 6,8
s2 = = 4,56
⇒ s = ≈ 2,14.
Câu 15. Nhiệt độ trung bình hàng tháng trong một năm được ghi lại trong bảng sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Nhiệt độ |
16 |
20 |
24 |
28 |
30 |
30 |
29 |
25 |
25 |
20 |
18 |
16 |
Tìm khoảng tứ phân vị của bảng số liệu trên.
A. 19,5;
B. 28,5;
C. 24,5;
D. 19.
Đáp án đúng là: B
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:
16 16 18 20 20 24 25 25 28 29 30 30
Trung vị của mẫu số liệu trên là: = 25 ⇒ Q2 = 24,5
Nửa dãy phía dưới số 24,5 ( nghĩa là những số nhỏ hơn 24,5) gồm: 16 16 18 20 20 24 có trung vị là = 19 ⇒ Q1 = 19.
Nửa dãy phía trên số 24,5 ( nghĩa là những số lớn hơn 24,5) gồm: 25 25 28 29 30 30 có trung vị là = 28,5 ⇒ Q3 = 28,5.
Do đó, tứ phân vị của mẫu số liệu: Q1 = 19; Q2 = 24,5; Q3 = 28,5
Vậy khoảng tứ phân vị của mẫu số liệu là: ∆Q = Q3 - Q1 = 28,5 – 19 = 9,5
Xem thêm bài tập trắc nghiệm Toán lớp 10 Cánh diều có đáp án hay khác:
Trắc nghiệm Toán 10 Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản
Trắc nghiệm Toán 10 Bài 5: Xác suất của biến cố
Trắc nghiệm Toán 10 Bài 1: Tọa độ của vectơ
Trắc nghiệm Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
Xem thêm các chương trình khác:
- Trắc nghiệm Toán lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Sinh học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Tin học lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Kinh tế pháp luật lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án - Global Success Kết nối tri thức
- Trắc nghiệm Toán lớp 10 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Chân trời sáng tạo
- Trắc nghiệm GDTC lớp 10 có đáp án – Chân trời sáng tạo