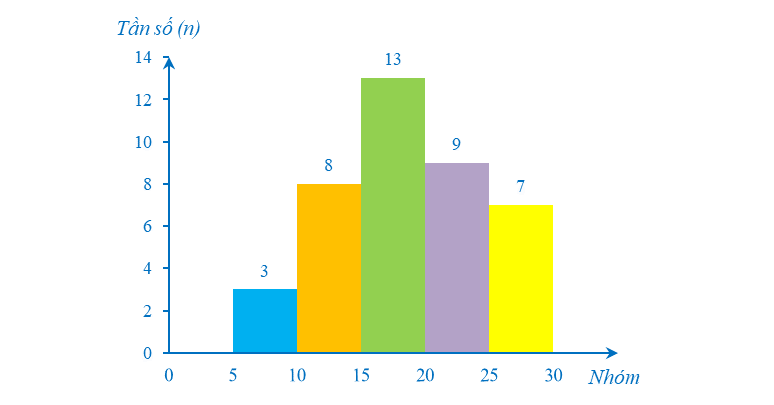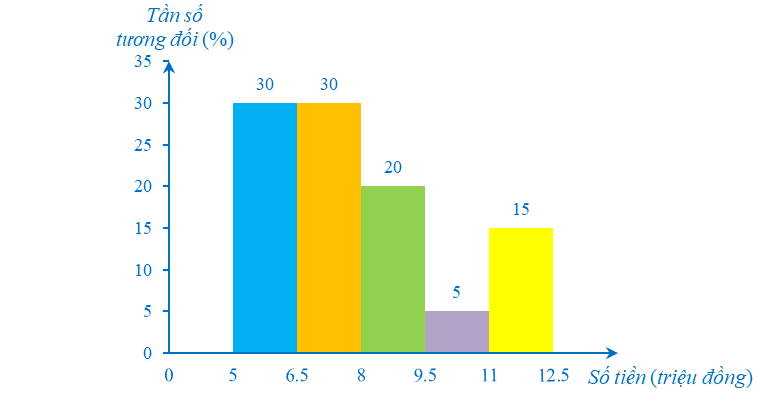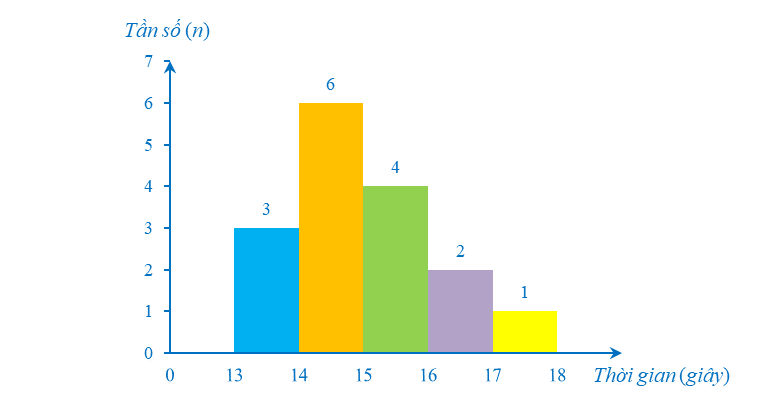Lý thuyết Tần số ghép nhóm. Tần số tương đối ghép nhóm - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 3: Tần số ghép nhóm. Tần số tương đối ghép nhóm

1. Mẫu số liệu ghép nhóm

– Khi mẫu số liệu có nhiều giá trị khác nhau nên nếu ta lập bảng tần số (hay bảng tần số tương đối) thì bảng sẽ rất dài, gây khó khăn trong việc phân tích, xử lí số liệu thu thập được. Để khắc phục trở ngại đó, ta có thể ghép các số liệu trên thành các nhóm.

– Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta có thể thực hiện như sau:

⦁ Tìm nửa khoảng [a; b) sao cho giá trị mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [a; b);

⦁ Ta thường phân chia nửa khoảng [a; b) thành các nửa khoảng có độ dài bằng nhau.

Chú ý: Khi ghép nhóm số liệu, đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu.

Ví dụ 1. Mẫu số liệu dưới đây ghi lại điểm kiểm tra của các học viên sau một khóa tập huấn:

$\begin{array}{cccccccccc}6,5& 2,4& 3,5& 6,8& 9,2& 7,6& 7,8& 9,3& 5,6& 9,5\\ 8,3& 8,2& 6,3& 9,1& 7,2& 4,7& 7& 7,4& 9,1& 9,9\\ 8,5& 7,5& 6,7& 2& 9& 8,7& 7,2& 3,2& 8,1& 6,4\end{array}$

Hãy ghép các số liệu trên thành bốn nhóm với bốn nửa khoảng có độ dài bằng nhau.

Hướng dẫn giải

Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là 2, số liệu có giá trị lớn nhất là 9,9.

Vì thế, ta có thể chọn nửa khoảng [2; 10) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [2; 10).

Vì độ dài của nửa khoảng [2; 10) bằng 10 – 2 = 8 nên ta có thể phân chia nửa khoảng đó thành bốn nửa khoảng có độ dài bằng nhau là: [2; 4), [4; 6), [6; 8), [8; 10).

Vậy ta có thể ghép nhóm mẫu số liệu đã cho theo bốn nhóm ứng với bốn nửa khoảng đó.

2. Tần số ghép nhóm. Bảng tần số ghép nhóm

– Trong một mẫu số liệu ghép nhóm, tần số ghép nhóm (hay tần số) của một nhóm là số số liệu trong mẫu số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là n₁, n₂, …, n_m.

– Để lập bảng tần số ghép nhóm ở dạng bảng ngang, ta có thể làm như sau:

Bước 1. Xác định các nhóm của mẫu dữ liệu ghép nhóm và tìm tần số của mỗi nhóm đó

Bước 2. Lập bảng gồm 2 dòng và một số cột

Theo thứ tự từ trên xuống dưới, ta lần lượt ghi:

⦁ Cột đầu tiên: Nhóm, Tần số (n)

⦁ Các cột tiếp theo lần lượt ghi tên nhóm và tần số của nhóm đó

⦁ Cột cuối cùng: Cộng, N = …

Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên.

Ví dụ 2. Xét mẫu số liệu sau:

$\begin{array}{cccccccccc}7& 11& 13,5& 20& 18,3& 25& 10,5& 22,9& 12,7& 15,1\\ 18,7& 16,3& 23,8& 28,1& 5& 24,8& 15& 17,8& 26,8& 20,6\\ 21,9& 27& 19,2& 14& 21,3& 16& 29,7& 28,6& 8,3& 18,9\\ 11,3& 17,2& 23,7& 19,5& 22,5& 12& 15& 17,4& 26,5& 14,9\end{array}$

a) Hãy ghép các số liệu trên thành năm nhóm ứng với năm nửa khoảng có độ dài bằng nhau. Tìm tần số của mỗi nhóm đó.

b) Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó.

Hướng dẫn giải

Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là 5, số liệu có giá trị lớn nhất là 29,7.

Vì thế, ta có thể chọn nửa khoảng [5; 30) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [5; 30).

Vì độ dài của nửa khoảng [5; 30) bằng 30 – 5 = 25 nên ta có thể phân chia nửa khoảng đó thành năm nửa khoảng có độ dài bằng nhau là: [5; 10), [10; 15), [15; 20), [20; 25), [25; 30).

Tần số của các nhóm [5; 10), [10; 15), [15; 20), [20; 25), [25; 30) lần lượt là:

n₁ = 3; n₂ = 8; n₃ = 13; n₄ = 9; n₅ = 7.

b) Bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó như sau:

Nhận xét:

⦁ Đối với một mẫu dữ liệu thống kê ghép nhóm, tần số của một nhóm phản ánh số lượng số liệu trong mẫu số liệu thuộc vào nhóm đó.

⦁ Cũng như mẫu số liệu không ghép nhóm, để trình bày mẫu số liệu ghép nhóm một cách trực quan, sinh động, dễ nhớ và gây ấn tượng, người ta sử dụng biểu đồ tần số ghép nhóm.

– Để vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của một mẫu số liệu ghép nhóm, ta có thể thực hiện theo các bước sau:

Bước 1.Lập bảng tần số ghép nhóm của mẫu số liệu được ghép nhóm đã cho

Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số ghép nhóm nhận được ở Bước 1 (các cột được ghép sát nhau).

Ví dụ 3. Vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ở Ví dụ 2.

Hướng dẫn giải

Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm ở Ví dụ 2 như sau:

3. Tần số tương đối ghép nhóm. Bảng tần số tương đối ghép nhóm. Biểu đồ tần số tương đối ghép nhóm

3.1. Tần số tương đối ghép nhóm và bảng tần số tương đối ghép nhóm

– Tần số tương đối ghép nhóm (hay tần số tương đối) f_i của nhóm i là tỉ số giữa tần số n_i của nhóm đó và số lượng N các số liệu trong mẫu số liệu thống kê: $f_i=\frac{n_i}{N}.$

Ta thường viết tần số tương đối ghép nhóm dưới dạng phần trăm.

– Để lập bảng tần số tương đối ghép nhóm ở dạng bảng ngang, ta có thể làm như sau:

Bước 1. Xác định các nhóm của mẫu dữ liệu ghép nhóm và tìm tần số tương đối của mỗi nhóm đó

Bước 2. Lập bảng gồm 2 dòng và một số cột

Theo thứ tự từ trên xuống dưới, ta lần lượt ghi:

⦁ Cột đầu tiên: Nhóm, Tần số tương đối (%)

⦁ Các cột tiếp theo lần lượt ghi nhóm và tần số tương đối của nhóm đó

⦁ Cột cuối cùng: Cộng, 100.

Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên.

Ví dụ 4. Số tiền (đơn vị: triệu đồng) chi tiêu cho sinh hoạt hàng tháng của một số hộ gia đình được thống kê như sau:

$\begin{array}{cccccccccc}9,1& 8,7& 11,7& 7,7& 5,8& 9,4& 5,4& 9,1& 6,4& 6,7\\ 11,8& 5,3& 6,9& 6,0& 10,0& 7,4& 6,9& 12,3& 5,9& 6,5\end{array}$

a) Hãy ghép các số liệu trên thành năm nhóm ứng với năm nửa khoảng sau:

[5; 6,5), [6,5; 8), [8; 9,5), [9,5; 11) [11; 12,5).

b) Lập bảng tần số ghép nhóm và bảng tấn số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

Hướng dẫn giải

a) Ghép các số liệu trên thành năm nhóm ứng với năm nửa khoảng đã cho, ta được:

b) Ta có bảng tần số ghép nhóm của mẫu số liệu đã cho như sau:

Tần số tương đối của các nhóm lần lượt là:

$f_1=f_2=\frac{6\cdot 100}{20}\%=30\%;f_3=\frac{4\cdot 100}{20}\%=20\%;$

$f_4=\frac{1\cdot 100}{20}\%=5\%;f_5=\frac{3\cdot 100}{20}\%=15\%.$

Ta có bảng tần số tương đối ghép nhóm của mẫu số liệu đã cho như sau:

3.2. Biểu đồ tần số tương đối ghép nhóm

– Để vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của một mẫu số liệu ghép nhóm, ta có thể thực hiện các bước sau:

Bước 1. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đã cho

Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số tương đối ghép nhóm nhận được ở Bước 1.

Ví dụ 5. Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm nhận được ở câu b trong Ví dụ 4.

Hướng dẫn giải:

Ta có biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm nhận được ở câu b trong Ví dụ 4 như sau:

– Để vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của một mẫu số liệu ghép nhóm, ta có thể thực hiện các bước sau:

Bước 1. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đã cho

Bước 2. Vẽ biểu đồ đoạn thẳng biểu diễn các số liệu thống kê trong bảng tần số tương đối ghép nhóm nhận được ở Bước 1.

Ví dụ 6. Cho bảng tần số và tần số tương đối ghép nhóm của một mẫu số liệu ghép nhóm:

a) Tìm các giá trị còn thiếu a, f­₁, f₄ trong bảng trên.

b) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm trong bảng trên.

Hướng dẫn giải

a) Ta có: N = 16 + 48 + 64 + a = 160. Do đó a = 32.

Các giá trị f₁ và f₄ lần lượt là: $f_1=\frac{16\cdot 100}{160}\%=10\%;f_4=\frac{32\cdot 100}{160}=20\%.$

b) Ta có bảng tần số tương đối ghép nhóm như sau:

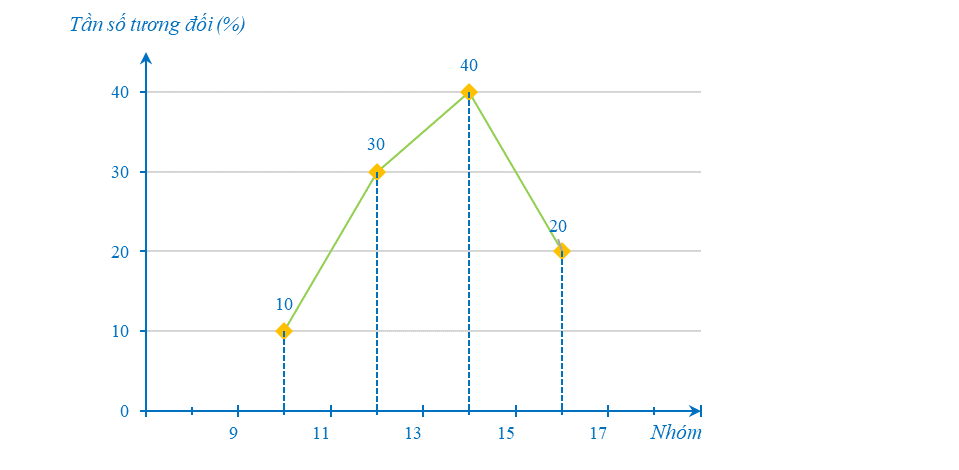
Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm trong bảng trên như sau:

Bài tập Tần số ghép nhóm. Tần số tương đối ghép nhóm

Bài 1. Bác Hoa đã thực hiện ghi lại thời gian tập thể dục của con trai mình mỗi ngày (đơn vị: giờ) trong vòng 30 ngày như sau:

$\begin{array}{cccccccccc}1,2& 3,7& 3,9& 3,2& 2,3& 2,1& 2,4& 3,5& 3,4& 2,7\\ 4,9& 2,7& 0,5& 1,5& 0,4& 2,0& 0,6& 1,8& 4,8& 1,5\\ 2,9& 2,4& 4,6& 3,5& 4,2& 1,7& 3,9& 2,4& 3,4& 1,6\end{array}$

Ghép mẫu số liệu trên thành các nhóm ứng với các nửa khoảng có độ dài bằng nhau thì nhóm [1; 2) có tần số là

A. 5;

B. 6;

C. 7;

D. 8.

Hướng dẫn giải

Đáp án đúng là: B

Ta thấy các giá trị thuộc nhóm [1; 2) là: 1,2; 1,5; 1,8; 1,5; 1,7; 1,6.

Vậy tần số của nhóm [1; 2) là 6.

Bài 2. Khối lượng (đơn vị: gam) của 30 quả cà chua thu hoạch được từ khu vườn của gia đình nhà An là:

$\begin{array}{cccccccccc}90& 73& 88& 93& 101& 104& 111& 95& 78& 95\\ 81& 97& 96& 95& 83& 90& 101& 103& 92& 117\\ 96& 86& 97& 82& 90& 75& 87& 112& 110& 109\end{array}$

Ghép các số liệu trên thành năm nhóm theo các nửa khoảng có độ dài bằng nhau, ta được các nhóm đó là:

A. [70; 80), [80; 90), [90; 100), [100; 110), [110; 120).

B. [75; 80), [80; 85), [85; 90), [90; 95), [95; 100).

C. [60; 75,5), [75,5; 90), [90; 100), [100; 110), [110; 120).

D. [70; 81), [81; 90), [91; 100), [91; 110), [111; 120).

Hướng dẫn giải

Đáp án đúng là: A

Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là 73, số liệu có giá trị lớn nhất là 117.

Vì thế, ta có thể chọn nửa khoảng [70; 120) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [70; 120).

Vì độ dài của nửa khoảng [70; 120) bằng 120 – 70 = 50 nên ta có thể phân chia nửa khoảng đó thành năm nửa khoảng có độ dài bằng nhau là:

[70; 80), [80; 90), [90; 100), [100; 110), [110; 120).

Vậy ta có thể ghép nhóm mẫu số liệu đã cho theo năm nhóm ứng với năm nửa khoảng đó.

Bài 3. Người ta tiến hành phỏng vấn 40 người về một mẫu sản phẩm mới. Người điều tra yêu cầu mỗi người được phỏng vấn cho điểm mẫu sản phẩm đó theo thang điểm là 100. Kết quả thống kê là như sau:

$\begin{array}{cccccccccc}50& 60& 62& 64& 71& 73& 70& 70& 70& 75\\ 75& 52& 55& 69& 80& 75& 75& 78& 79& 73\\ 55& 72& 71& 85& 82& 90& 78& 78& 75& 75\\ 65& 85& 87& 77& 81& 79& 99& 75& 70& 72\end{array}$

Khi vẽ biểu đồ bảng tần số tương đối ghép nhóm dạng đoạn thẳng, điểm M(85; 6) ứng với nhóm số liệu nào:

A. [60; 70).

B. (70; 80);

C. [80; 90);

D. [90; 100).

Hướng dẫn giải

Đáp án đúng là: C

Giá trị đại diện của các nhóm lần lượt là: $x_1=\frac{50+60}{2}=55;$$x_2=\frac{60+70}{2}=65;$$x_3=\frac{70+80}{2}=75;$$x_4=\frac{80+90}{2}=85;$$x_5=\frac{90+100}{2}=95.$

Tần số ghép nhóm của nhóm [80; 90) là 6 nên khi vẽ biểu đồ bảng tần số tương đối ghép nhóm dạng đoạn thẳng, điểm M(85; 6) ứng với nhóm [80; 90).

Bài 4. Cho biểu đồ biểu diễn kết quả khảo sát thành tích chạy của 100 m của một số học sinh như sau:

a) Có bao nhiêu học sinh chạy hết 100 m ít hơn 15 giây?

b) Có tổng số bao nhiêu học sinh tham gia khảo sát?

Hướng dẫn giải

a) Dựa vào biểu đồ trên, ta thấy số học sinh chạy hết 100 m ít hơn 15 giây chính là tổng số học sinh của hai nhóm [13; 14), [14, 15).

Số học sinh chạy hết 100 m ít hơn 15 giây là: 3 + 6 = 9 (học sinh).

b) Tổng số học sinh tham gia khảo sát là: 3 + 6 + 4 + 2 = 16 (học sinh).

Bài 5. Thầy Hải đang thực hiện thống kê về số điểm trung bình môn Toán thi vào lớp 10 của học sinh khối 9 tại một trường trung học cơ sở. Do sơ suất nên thầy Hải đã ghi thiếu một số số liệu. Em hãy giúp thầy hoàn thành bảng thống kê sau:

Hướng dẫn giải

Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là 4, số liệu có giá trị lớn nhất là 10. Vì độ dài của nửa khoảng [4; 10) bằng 10 – 4 = 6 mà có 3 nhóm nên ta có thể ghép nhóm mẫu số liệu đã cho theo ba nhóm ứng với ba nửa khoảng bằng 2 đó là:

[4; 6), [6; 8), [8; 10).

Ta có công thức tính tần số tương đối ghép nhóm của nhóm [4; 6) là:

$f_1=\frac{n_1\cdot 100}{N}\%,$ suy ra $10\%=\frac{20\cdot 100}{N}\%,$ do đó N = 200.

Khi đó, ta có tần số tương đối ghép nhóm của nhóm [6; 8) là:

100% – 10% – 25% = 65%.

Tần số ghép nhóm của nhóm [6; 8) là:

$f_2=\frac{n_2\cdot 100}{200}\%=65\%,$ suy ra n₂ = 130.

Tần số ghép nhóm của nhóm [8; 10) là: 200 – 20 – 130 = 50.

Ta có bảng tần số ghép nhóm và tần số tương đối ghép nhóm như sau:

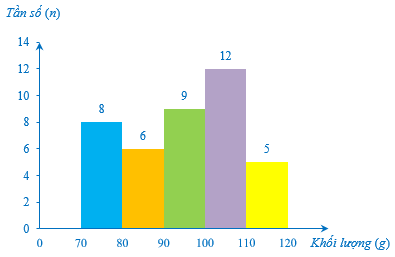
Bài 6. Khối lượng (đơn vị: gam) của một số quả cà chua thu hoạch được từ khu vườn của gia đình An như sau:

a) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

b) Vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm câu a.

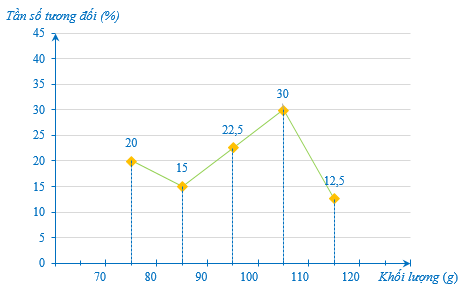
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm câu a.

Hướng dẫn giải

a) Ta thấy rằng tổng số quả là N = 8 + 6 + 9 + 12 + 5 = 40.

Tần số tương đối ghép nhóm của của các nhóm [70; 80), [80; 90), [90; 100), [100; 110), [110; 120) lần lượt là: $f_1=\frac{8\cdot 100}{40}\%=20\%,$$f_2=\frac{6\cdot 100}{40}\%=15\%,$$f_3=\frac{9\cdot 100}{40}\%=22,5\%,$$f_4=\frac{12\cdot 100}{40}\%=30\%,$$f_5=\frac{5\cdot 100}{40}\%=12,5\%.$

Ta có bảng sau:

b) Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu đã cho như sau:

c) Biểu đồ tần số ghép nhóm ở dạng biểu đoạn thẳng của mẫu số liệu đã cho như sau: