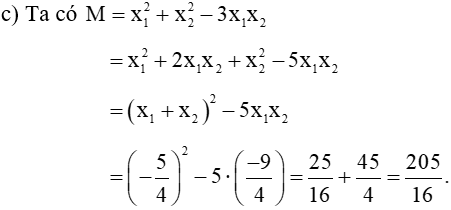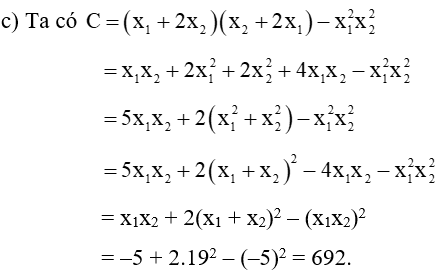Lý thuyết Định lí Viète - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 3: Định lí Viète

1. Định lí Viète

Định lí Viète chỉ ra mối liên hệ giữa tổng và tích của hai nghiệm với các hệ số của phương trình bậc hai một ẩn:

Nếu x₁, x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì

$x_1+x_2=-\frac{b}{a};x_1{x}_2=\frac{c}{a}.$

Ví dụ 1. Cho phương trình 4x² + 5x – 9 = 0.

a) Chứng minh phương trình trên có hai nghiệm phân biệt x₁, x₂.

b) Tính tổng và tích các nghiệm của phương trình trên.

c) Tính $M=x_1^2+x_2^2-3x_1{x}_2.$

Hướng dẫn giải

a) Phương trình đã cho có các hệ số a = 4; b = 5; c = –9.

Ta có: ∆ = b² – 4ac = 5² – 4.4.(–9) = 169 > 0.

Vậy phương trình đã cho có hai nghiệm phân biệt x₁, x₂.

b) Theo định lí Viète, ta có:

$x_1+x_2=-\frac{b}{a}=-\frac{5}{4};x_1{x}_2=\frac{c}{a}=\frac{-9}{4}.$

Vậy $M=\frac{205}{16}.$

Ví dụ 2. Cho phương trình –3x² + 10x – 7 = 0.

a) Xác định các hệ số a, b, c của phương trình trên. Từ đó tính a + b + c.

b) Chứng tỏ x₁ = 1 là một nghiệm của phương trình.

c) Dùng định lí Viète để tìm nghiệm x₂ còn lại của phương trình.

Hướng dẫn giải

a) Phương trình –3x² + 10x – 7 = 0 có các hệ số a = –3; b = 10; c = –7.

Suy ra a + b + c = –3 + 10 + (–7) = 0.

b) Ta có: –3.1² + 10.1 – 7 = 0.

Vậy x₁ = 1 là một nghiệm của phương trình.

c) Theo định lí Viète, ta có: $x_1{x}_2=\frac{c}{a}=\frac{-7}{-3}=\frac{7}{3}.$

Với x₁ = 1, ta có: $1\cdot x_2=\frac{7}{3}.$ Suy ra $x_2=\frac{7}{3}.$

Vậy nghiệm còn lại của phương trình là $x_2=\frac{7}{3}.$

Ví dụ 3. Cho phương trình 6x² + 31x + 25 = 0.

a) Xác định các hệ số a, b, c của phương trình trên. Từ đó tính a – b + c.

b) Chứng tỏ x₁ = –1 là một nghiệm của phương trình.

c) Dùng định lí Viète để tìm nghiệm x₂ còn lại của phương trình.

Hướng dẫn giải

a) Phương trình 6x² + 31x + 25 = 0 có các hệ số a = 6; b = 31; c = 25.

Suy ra a – b + c = 6 – 31 + 25 = 0.

b) Ta có: 6.(–1)² + 31.(–1) + 25 = 0.

Vậy x₁ = –1 là một nghiệm của phương trình.

c) Theo định lí Viète, ta có: $x_1{x}_2=\frac{c}{a}=\frac{25}{6}.$

Với x₁ = –1, ta có: $\left(-1\right)\cdot x_2=\frac{25}{6}.$Suy ra $x_2=-\frac{25}{6}.$

Vậy nghiệm còn lại của phương trình là $x_2=-\frac{25}{6}.$

Nhận xét:

⦁ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1 và nghiệm còn lại là $x_2=\frac{c}{a}.$

⦁ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x₁ = –1 và nghiệm còn lại là $x_2=-\frac{c}{a}.$

Ví dụ 4. Không tính ∆, giải các phương trình sau:

a) $\frac{2}{5}{x}^2-2x+\frac{8}{5}=0;$

b) $2\sqrt{3}{x}^2+\left(1+\sqrt{3}\right)x+1-\sqrt{3}=0.$

Hướng dẫn giải

a) Phương trình đã cho có các hệ số $a=\frac{2}{5};b=-2;c=\frac{8}{5}.$

Ta thấy: $a+b+c=\frac{2}{5}+\left(-2\right)+\frac{8}{5}=0.$

Vậy phương trình đã cho có nghiệm là x₁ = 1 và $x_2=\frac{8}{5}:\frac{2}{5}=\frac{8}{5}\cdot \frac{5}{2}=4.$

b) Phương trình đã cho có các hệ số $a=2\sqrt{3};b=1+\sqrt{3};c=1-\sqrt{3}.$

Ta thấy: $a-b+c=2\sqrt{3}-\left(1+\sqrt{3}\right)+1-\sqrt{3}=0.$

Vậy phương trình đã cho có nghiệm là x₁ = –1 và $x_2=-\frac{1-\sqrt{3}}{2\sqrt{3}}=\frac{\left(\sqrt{3}-1\right)\sqrt{3}}{2\sqrt{3}\cdot \sqrt{3}}=\frac{3-\sqrt{3}}{6}.$

2. Tìm hai số khi biết tổng và tích

Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình

x²– Sx + P = 0.

Chú ý: Điều kiện để có hai số đó là S² – 4P ≥ 0.

Ví dụ 5. Tìm hai số (nếu có) trong mỗi trường hợp sau:

a) Tổng của chúng bằng 10 và tích của chúng bằng 9;

b) Tổng của chúng bằng –3 và tích của chúng bằng 14.

Hướng dẫn giải

a) Hai số cần tìm là nghiệm của phương trình x² – 10x + 9 = 0(1)

Phương trình (1) có các hệ số a = 1; b = –10; c = 9.

Vì b = –10 nên b’ = –5.

Ta có: ∆’ = b’² – ac = (–5)² – 1.9 = 16 > 0 và $\sqrt{{\Delta }^{\text{'}}}=\sqrt{16}=4.$

Do đó, phương trình (1) có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-5\right)+4}{1}=9;x_2=\frac{-\left(-5\right)-4}{1}=1.$

Vậy hai số cần tìm là 9 và 1.

b) Theo đề, ta có S = –3 và P = 14.

Ta thấy: S² – 4P = (–3)² – 4.14 = –47 < 0.

Vậy không tồn tại hai số thỏa mãn điều kiện đã cho.

Bài tập Định lí Viète

Bài 1. Phương trình x² + bx + c = 0 thỏa mãn b + c = –1 thì có hai nghiệm là

A. x₁ = 1 và x₂ = c;

B. x₁ = –1 và x₂ = –c;

C. x₁ = 2 và x₂ = b;

D. x₁ = x₂ = b.

Hướng dẫn giải

Đáp án đúng là: A

Xét phương trình x² + bx + c = 0 có hệ số a = 1.

Ta thấy a + b + c = 1 + b + c = 1 + (–1) = 0.

Suy ra phương trình đã cho có hai nghiệm là x₁ = 1 và $x_2=\frac{c}{a}=\frac{c}{1}=c.$

Vậy ta chọn phương án A.

Bài 2. Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình x² – 3x + 2 = 0. Khi đó giá trị của S và P là

A. S = –3 và P = 2;

B. S = 2 và P = 3;

C. S = 3 và P = –2;

D. S = 3 và P = 2.

Hướng dẫn giải

Đáp án đúng là: D

Phương trình đã cho có các hệ số a = 1; b = –3; c = 2.

Theo định lí Viète, ta có:

$S=x_1+x_2=-\frac{b}{a}=-\frac{-3}{1}=3$ và $P=x_1{x}_2=\frac{c}{a}=\frac{2}{1}=2.$

Vậy S = 3 và P = 2.

Do đó ta chọn phương án D.

Bài 3. Điều kiện tồn tại hai số có tổng bằng S và tích bằng P là

A. S² – 4P ≥ 0;

B. S² ≥ P;

C. S² + 4P ≥ 0;

D. P² + 4S ≥ 0.

Hướng dẫn giải

Đáp án đúng là: A

Điều kiện để có hai số có tổng bằng S và tích bằng P là S² – 4P ≥ 0.

Vậy ta chọn phương án A.

Bài 4. Không tính ∆, giải các phương trình sau:

a) –x² + 7x – 6 = 0;

b) 5x² + 8x + 3 = 0;

c) 11x² + 18x – 45 = 0, biết phương trình có một nghiệm x₁ = –3.

Hướng dẫn giải

a) Phương trình –x² + 7x – 6 = 0 có các hệ số a = –1; b = 7; c = –6.

Suy ra a + b + c = –1 + 7 + (–6) = 0.

Do đó phương trình –x² + 7x – 6 = 0 có nghiệm x₁ = 1 và $x_2=\frac{c}{a}=\frac{-6}{-1}=6.$

Vậy phương trình đã cho có hai nghiệm là x₁ = 1 và x₂ = 6.

b) Phương trình 5x² + 8x + 3 = 0 có các hệ số a = 5; b = 8; c = 3.

Suy ra a – b + c = 5 – 8 + 3 = 0.

Do đó phương trình 5x² + 8x + 3 = 0 có nghiệm x₁ = –1 và $x_2=-\frac{c}{a}=-\frac{3}{5}.$

Vậy phương trình đã cho có hai nghiệm là x₁ = –1 và $x_2=-\frac{3}{5}.$

c) Phương trình 11x² + 18x – 45 = 0 có các hệ số a = 11; b = 18; c = –45.

Theo định lí Viète, ta có $x_1{x}_2=\frac{c}{a}=\frac{-45}{11}.$

Với x₁ = –3, ta có: $-3\cdot x_2=\frac{-45}{11}.$ Suy ra $x_2=\frac{15}{11}.$

Vậy phương trình đã cho có hai nghiệm là x₁ = –3 và $x_2=\frac{15}{11}.$

Bài 5. Cho phương trình x² – 19x – 5 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức:

a) A = (x₁ – x₂)²;

b) $B=\frac{2}{x_1+5}+\frac{2}{x_2+5};$

c) $C=\left(x_1+2x_2\right)\left(x_2+2x_1\right)-x_1^2{x}_2^2.$

Hướng dẫn giải

a) Phương trình x² – 19x – 5 = 0 có các hệ số a = 1; b = –19; c = –5.

Ta có: ∆ = b² – 4ac = (–19)² – 4.1.(–5) = 381 > 0.

Do đó phương trình đã cho có hai nghiệm phân biệt x₁, x₂.

Theo định lí Viète, ta có: $x_1+x_2=-\frac{-19}{1}=19;x_1{x}_2=\frac{-5}{1}=-5.$

Ta có $A={\left(x_1-x_2\right)}^2=x_1^2+x_2^2-2x_1{x}_2={\left(x_1+x_2\right)}^2–4x_1{x}_2={19}^2–4\cdot \left(–5\right)=381.$

Vậy A = 381.

b) Ta có $B=\frac{2}{x_1+5}+\frac{2}{x_2+5}=\frac{2\left(x_2+5\right)+2\left(x_1+5\right)}{\left(x_1+5\right)\left(x_2+5\right)}$

$=\frac{2\left(x_1+x_2+10\right)}{x_1{x}_2+5\left(x_1+x_2\right)+25}=\frac{2\left(19+10\right)}{-5+5\cdot 19+25}=\frac{58}{115}.$

Vậy $B=\frac{58}{115}.$

Vậy C = 692.

Bài 6. Một bể bơi hình chữ nhật có diện tích 90 m² và chu vi 42 m. Tính chiều dài, chiều rộng của bể bơi đó.

Hướng dẫn giải

Nửa chu vi của bể bơi là: 42 : 2 = 21 (m). Do đó tổng của chiều dài và chiều rộng bể bơi bằng 21 mét.

Lại có diện tích của bể bơi là 90 m², tức là tích của chiều dài và chiều rộng bể bơi bằng 90 m².

Chiều dài và chiều rộng của bể bơi có tổng bằng 21 và tích bằng 90 nên hai độ dài này là hai nghiệm của phương trình: x² – 21x + 90 = 0. (1)

Phương trình (1) có các hệ số a = 1; b = –21; c = 90.

Ta có: ∆ = b² – 4ac = (–21)² – 4.1.90 = 81 > 0 và $\sqrt{\Delta }=\sqrt{81}=9.$

Do đó, phương trình (1) có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-21\right)+9}{2\cdot 1}=\frac{21+9}{2}=15;$

$x_2=\frac{-\left(-21\right)-9}{2\cdot 1}=\frac{21-9}{2}=6.$

Vậy chiều dài, chiều rộng của bể bơi đó lần lượt là 15 m và 6 m (do chiều rộng nhỏ hơn chiều dài).