Lý thuyết Một số phép biến đổi căn thức bậc hai của biểu thức đại số - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

1. Căn thức bậc hai của một bình phương

Quy tắc: Với mỗi biểu thức A, ta có $\sqrt{A^2}=\left|A\right|,$ tức là:

$\sqrt{A^2}=\left|A\right|=A$ nếu A ≥ 0;

$\sqrt{A^2}=\left|A\right|= -A$ nếu A < 0.

Ví dụ 1. Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức sau:

a) $\sqrt{4x^2+4\text{x}+1}$ với x > 0;

b) $\sqrt{x^2\cdot x^4}$ với x < 0.

Hướng dẫn giải

a) $\sqrt{4x^2+4\text{x}+1}=\sqrt{{\left(2\text{x}+1\right)}^2}=\left|2\text{x}+1\right|=2\text{x}+1$ (vì x > 0 thì 2x + 1 > 0);

b) $\sqrt{x^2\cdot x^4}=\sqrt{x^6}=\sqrt{{\left(x^3\right)}^2}=\left|x^3\right|=-x^3$ (vì x < 0 nên x³ < 0).

2. Căn thức bậc hai của một tích

Quy tắc: Với các biểu thức A, B không âm, ta có $\sqrt{A\cdot B}=\sqrt{A}\cdot \sqrt{B}.$

Ví dụ 2.Áp dụng quy tắc về căn thức bậc hai của một tích, hãy rút gọn biểu thức sau:

a) $\sqrt{9\text{x}}\cdot \sqrt{9{\text{x}}^3}$ với x > 0.

b) $\sqrt{0,49a\cdot 0,25a}$ với a < 0.

Hướng dẫn giải

a) $\sqrt{9\text{x}}\cdot \sqrt{9{\text{x}}^3}=\sqrt{9\text{x}\cdot 9{\text{x}}^3}=\sqrt{81{\text{x}}^4}=\sqrt{{\left(9x^2\right)}^2}=\left|9x^2\right|=9{\text{x}}^2$ (vì x² > 0 với mọi x > 0);

b) $\sqrt{0,49a\cdot 0,25a}=\sqrt{0,49}\cdot \sqrt{0,25}\cdot \sqrt{a^2}=0,7\cdot 0,5\cdot \left|a\right|=-0,35\text{a}$ (vì a < 0).

3. Căn thức bậc hai của một thương

Quy tắc: Với biểu thức A không âm và biểu thức B dương, ta có $\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}.$

Ví dụ 3.Áp dụng quy tắc về căn thức bậc hai của một thương, hãy rút gọn biểu thức sau:

a) $\sqrt{\frac{1}{x^2}}$ với x < 0;

b) $\frac{\sqrt{{\text{144x}}^5}}{\sqrt{36{\text{x}}^3}}$ với x > 0.

Hướng dẫn giải

a) $\sqrt{\frac{1}{x^2}}=\frac{\sqrt{1}}{\sqrt{x^2}}=\frac{1}{\left(x\right)}=\frac{1}{-x}$ (vì x < 0);

b) $\frac{\sqrt{{\text{144x}}^5}}{\sqrt{36{\text{x}}^3}}=\sqrt{\frac{144{\text{x}}^5}{36{\text{x}}^3}}=\sqrt{4{\text{x}}^2}=\sqrt{{\left(2x\right)}^2}=\left|2x\right|=2\text{x}$ ( vì x > 0)

4. Trục căn thức ở mẫu

Phép biến đổi làm mất căn thức ở mẫu thức của một biểu thức được gọi là trục căn thức ở mẫu của biểu thức đó.

Chú ý: Các biểu thức A, B mà B > 0, ta có: $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}.$

Ví dụ 4. Trục căn thức ở mẫu của biểu thức $\frac{x-1}{\sqrt{2\text{x}}}.$

Hướng dẫn giải

Ta có: $\frac{x-1}{\sqrt{2\text{x}}}=\frac{\left(x-1\right)\sqrt{2\text{x}}}{2\text{x}}=\frac{x\sqrt{2\text{x}}-\sqrt{2\text{x}}}{2\text{x}}.$

Chú ý: Các biểu thức A, B, C mà B ≥ 0 và A² ≠ B, ta có:

$\frac{C}{A+\sqrt{B}}=\frac{C\left(A-\sqrt{B}\right)}{A^2-B};\frac{C}{A-\sqrt{B}}=\frac{C\left(A+\sqrt{B}\right)}{A^2-B}.$

Lưu ý: $A-\sqrt{B}$ được gọi là biểu thức liên hợp của $A+\sqrt{B}$ và ngược lại.

Ví dụ 5. Trục căn thức ở mẫu: $\frac{2}{\sqrt{2}+1}.$

Hướng dẫn giải

Ta có: $\frac{2}{\sqrt{2}+1}=\frac{2\left(\sqrt{2}-1\right)}{\left(\sqrt{2+1}\right)\left(\sqrt{2}-1\right)}=\frac{2\sqrt{2}-2}{{\left(\sqrt{2}\right)}^2-1^2}=\frac{2\sqrt{2}-2}{2-1}=2\sqrt{2}-2.$

Chú ý: Các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B, ta có:

$\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left(\sqrt{A}-\sqrt{B}\right)}{A-B};\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left(\sqrt{A}+\sqrt{B}\right)}{A-B}.$

Lưu ý: $\sqrt{A}-\sqrt{B}$ được gọi là biểu thức liên hợp của $\sqrt{A}+\sqrt{B}$ và ngược lại.

Ví dụ 6.Trục căn thức ở mẫu: $\frac{6}{\sqrt{5}-\sqrt{2}}.$

Hướng dẫn giải

Ta có: $\frac{6}{\sqrt{5}-\sqrt{2}}=\frac{6\left(\sqrt{5}+\sqrt{2}\right)}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)}=\frac{6\left(\sqrt{5}+\sqrt{2}\right)}{{\left(\sqrt{5}\right)}^2-{\left(\sqrt{2}\right)}^2}$

$=\frac{6\left(\sqrt{5}+\sqrt{2}\right)}{5-2}=\frac{6\left(\sqrt{5}+\sqrt{2}\right)}{3}=2\sqrt{5}+2\sqrt{2}.$

Sơ đồ tư duy Một số phép biến đổi căn thức bậc hai của biểu thức đại số

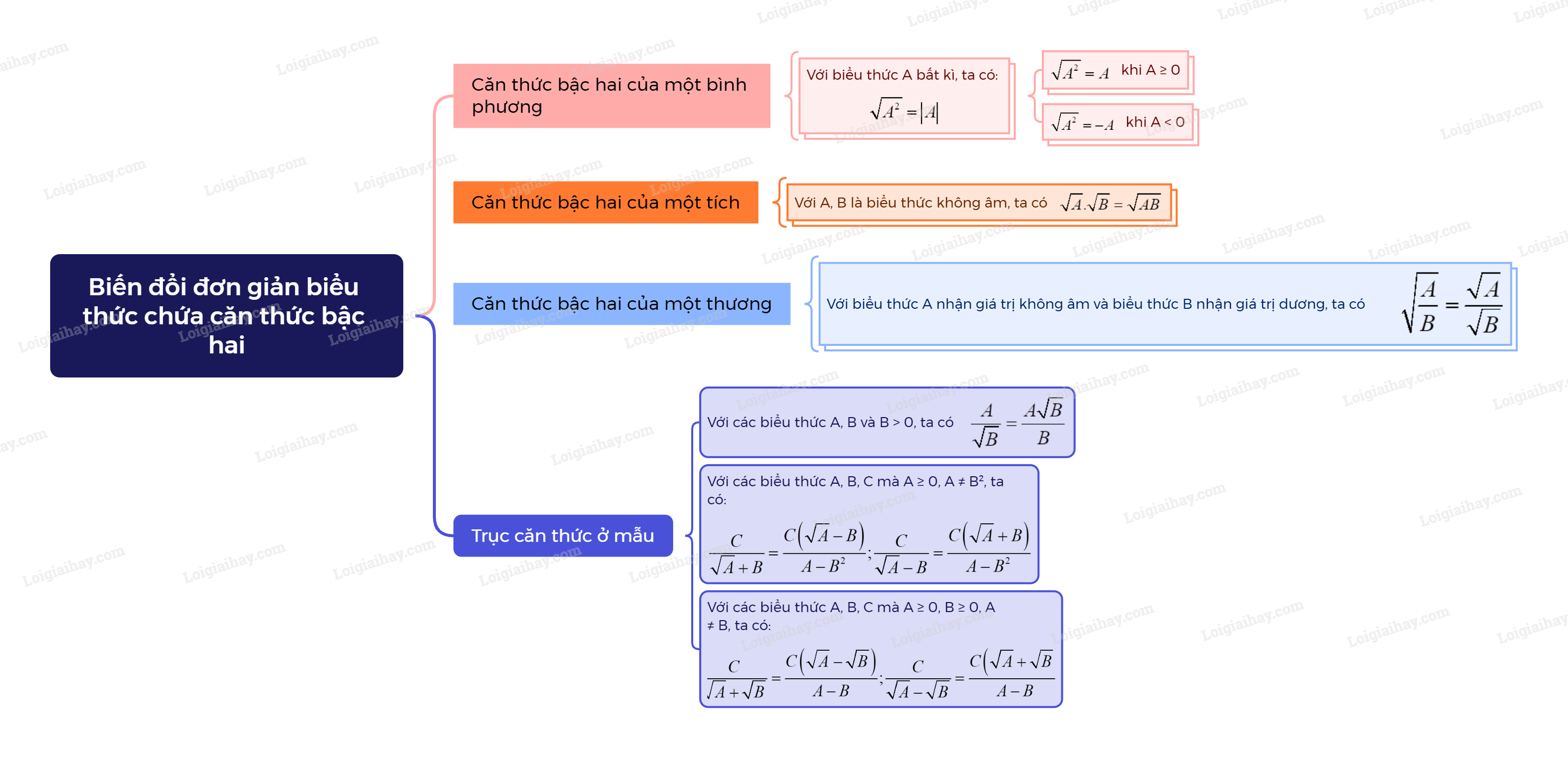
Bài tập Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài 1.Cho các biểu thức A < 0 và B ≥ 0, khẳng định nào sau đây là đúng?

A. $\sqrt{A^{2}B}=A\sqrt{B};$

B. $\sqrt{A^{2}B}=-A\sqrt{B};$

C. $\sqrt{A^{2}B}=-B\sqrt{A};$

D. $\sqrt{A^{2}B}=B\sqrt{A}.$

Hướng dẫn giải

Đáp án đúng là:B

Ta có: $\sqrt{A^{2}B}=\sqrt{A^2}\cdot \sqrt{B}=-A\sqrt{B}$ (vì A < 0).

Vậy ta chọn phương án B.

Bài 2. Trục căn thức ở mẫu của biểu thức $\frac{4}{3\sqrt{x}+2\sqrt{y}}$ với x ≥ 0, y ≥ 0 và $x\ne \frac{4}{9}y$ ta được

A. $\frac{3\sqrt{x}-2\sqrt{y}}{9x-4y};$

B. $\frac{12\sqrt{x}-8\sqrt{y}}{3x+2y};$

C. $\frac{12\sqrt{x}+8\sqrt{y}}{9x+4y};$

D. $\frac{12\sqrt{x}-8\sqrt{y}}{9x-4y}.$

Hướng dẫn giải

Đáp án đúng là: D

Với x ≥ 0, y ≥ 0 và $x\ne \frac{4}{9}y$ ta có:

$\frac{4}{3\sqrt{x}+2\sqrt{y}}=\frac{4\left(3\sqrt{x}-2\sqrt{y}\right)}{\left(3\sqrt{x}+2\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)}$

$=\frac{12\sqrt{x}-8\sqrt{y}}{{\left(3\sqrt{x}\right)}^2-{\left(2\sqrt{y}\right)}^2}=\frac{12\sqrt{x}-8\sqrt{y}}{9x-4y}.$

Bài 3.Rút gọn biểu thức $\frac{a}{\sqrt{5}+1}+\frac{a}{\sqrt{5}-2}-\frac{a}{3-\sqrt{5}}-\sqrt{5}a$ ta được:

A. 2a;

B. a;

C. 3a;

D. 12a.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\frac{a}{\sqrt{5}+1}+\frac{a}{\sqrt{5}-2}-\frac{a}{3-\sqrt{5}}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}+\frac{a\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\frac{a\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{5-1}+\frac{a\left(\sqrt{5}+2\right)}{5-4}-\frac{a\left(3+\sqrt{5}\right)}{9-5}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{4}+a\left(\sqrt{5}+2\right)-\frac{a\left(3+\sqrt{5}\right)}{4}-\sqrt{5}a$

$=\frac{a\sqrt{5}-a-3\text{a}-a\sqrt{5}}{4}+a\sqrt{5}+2\text{a}-a\sqrt{5}$

$=\frac{-4\text{a}}{4}+2\text{a=}-a+2\text{a}=a.$

Vậy ta chọn đáp án B.

Bài 4.Rút gọn các biểu thức sau:

a) $\sqrt{225\left(x^2-4x+4\right)}$ với x ≥ 2;

b) $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}$ với x < y.

Hướng dẫn giải

a) Ta có: $\sqrt{225\left(x^2-4x+4\right)}=\sqrt{{15}^2\cdot {\left(x-2\right)}^2}$

$=\sqrt{{15}^2}\cdot \sqrt{{\left(x-2\right)}^2}=15\left|x-2\right|.$

Với x ≥ 2 thì x – 2 ≥ 0 nên |x – 2| = x – 2.

Do đó $\sqrt{225\left(x^2-4x+4\right)}=15\left|x-2\right|=15\left(x-2\right)=15x-30$

Vậy $\sqrt{225\left(x^2-4x+4\right)}=15x-30$ với x ≥ 2.

b) Cách 1:

Ta có: $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\sqrt{x^4}\cdot \sqrt{{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|$

Với x < y thì x – y < 0 nên |x – y| = – (x – y).

Do đó $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|=\frac{3}{x-y}\cdot x^2\cdot \left[-\left(x-y\right)\right]=-3x^2.$

Vậy $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=-3x^2$ với x < y.

Cách 2: Với x < y thì x – y < 0 nên ta có:

$\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=3\cdot \sqrt{x^4}\cdot \frac{1}{x-y}\cdot \sqrt{{\left(x-y\right)}^2}$

$=-3x^2\sqrt{\frac{1}{{\left(x-y\right)}^2}\cdot {\left(x-y\right)}^2}=-3x^2.$

Bài 5.Rút gọn biểu thức: $P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.$

Hướng dẫn giải

$P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left[\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]:\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left(-\sqrt{7}-\sqrt{5}\right)\cdot \left(\sqrt{7}-\sqrt{5}\right)$

$=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)$

= –(7 – 5) = –2.

Bài 6.Cho $A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$ với x ≥ 0, x ≠ 4.

a) Rút gọn biểu thức A.

b) Tìm x sao cho A < 2.

Hướng dẫn giải

a)Với x ≥ 0, x ≠ 4, ta có:

$A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$

$=\left[\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{{\left(\sqrt{x}\right)}^3-2^3}\right]\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{\sqrt{x}\left(x+2\sqrt{x}+4\right)-\left(x-3\right)\left(\sqrt{x}-2\right)-7\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{x\sqrt{x}+2x+4\sqrt{x}-x\sqrt{x}+2x+3\sqrt{x}-6-7\sqrt{x}-10}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4x-16}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}=\frac{4\left(x-4\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

Vậy với x ≥ 0, x ≠ 4 thì $A=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

b)Với x ≥ 0, x ≠ 4, ta có A < 2 nên $\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

Giải bất phương trình:

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}-2<0$

$\frac{4\left(\sqrt{x}+2\right)-2\left(\sqrt{x}+7\right)}{\sqrt{x}+7}<0$

$4\sqrt{x}+8-2\sqrt{x}-14<0$ (Do $\sqrt{x+7}>0)$

$2\sqrt{x}<6$

$\sqrt{x}<3$

x < 9.

Kết hợp điều kiện xác định ta được 0 ≤ x < 9 và x ≠ 4.