Lý thuyết Phép quay - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 2: Phép quay

1. Khái niệm

Cho điểm O cố định và số thực α.

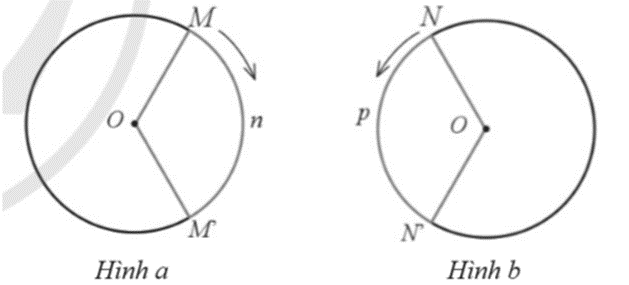
– Phép quay thuận chiều α° (0° < α° < 360°) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo α° (Hình a).

– Phép quay ngược chiều α° (0° < α° < 360°) tâm O được phát biểu tương tự (Hình b).

Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.

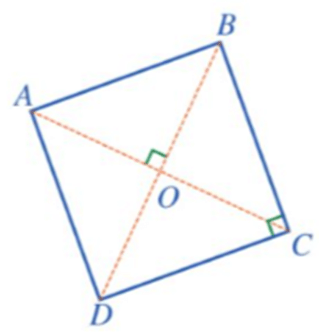
Ví dụ 1. Cho hình vuông ABCD tâm O.

a) Chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến các điểm A, B, C, D theo thứ tự thành các điểm B, C, D, A.

b) Phép quay ngược chiều 180° tâm O biến các điểm A, B, C, D thành các điểm nào?

Hướng dẫn giải

a) Vì ABCD là hình vuông nên AC ⊥ BD tại O.

Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D theo thứ tự thành các điểm B, C, D, A.

b) Phép quay ngược chiều 180° tâm O biến các điểm A, B, C, D theo thứ tự thành các điểm C, D, A, B.

2. Phép quay giữ nguyên hình đa giác đều

– Cho hình đa giác đều A₁A₂...A_n (n ≥ 3, n ∈ ℕ) có tâm O. Phép quay giữ nguyên hình đa giác đều A₁A₂...A_n là phép quay tâm O biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó.

– Các phép quay giữ nguyên hình đa giác đều A₁A₂...A_n (n ≥ 3, n ∈ ℕ) với tâm O là các phép quay thuận chiều α° tâm O và các phép quay ngược chiều α° tâm O, với α° lần lượt nhận các giá trị

${\alpha }_1^o=\frac{360°}{n};{\alpha }_2^o=\frac{2\cdot 360°}{n};\mathrm{...};{\alpha }_n^o=\frac{n\cdot 360°}{n}=360°.$

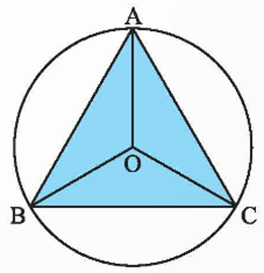
Ví dụ 2. Cho tam giác ABC đều nội tiếp đường tròn (O). Chỉ ra các phép quay giữ nguyên tam giác ABC.

Hướng dẫn giải

Các phép quay giữ nguyên tam giác ABC là:

⦁ Ba phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị:

${\alpha }_1^o=\frac{360°}{3}=120°;{\alpha }_2^o=\frac{2\cdot 360°}{3}=240°;{\alpha }_3^o=\frac{3\cdot 360°}{3}=360°.$

⦁ Ba phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị:

${\alpha }_1^o=\frac{360°}{3}=120°;{\alpha }_2^o=\frac{2\cdot 360°}{3}=240°;{\alpha }_3^o=\frac{3\cdot 360°}{3}=360°.$

Bài tập Phép quay

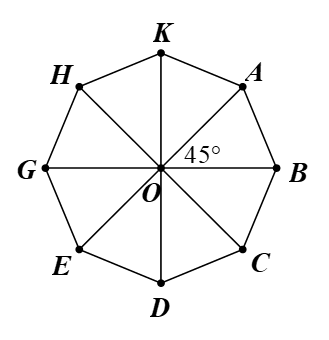
Bài 1. Cho bát giác đều ABCDEFGH có tâm O. Phép quay thuận chiều 135° tâm O biến điểm D của bát giác đều ABCDEFGH thành điểm nào?

A. G;

B. A;

C. E;

D. H.

Hướng dẫn giải

Đáp án đúng là: A

Giả sử ABCDEGHK là bát giác đều có tâm O.

Do đó AB = BC = CD = DE = EG = GH = HK và OA = OB = OC = OD = OE = OG = OH = OK.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC

Do đó ∆OAB = ∆OBC (c.c.c).

Tương tự, ta sẽ chứng minh được:

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.

Suy ra các góc tương ứng bằng nhau:

$\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOG}=\widehat{GOH}=\widehat{HOK}=\widehat{KOA}.$

Ta có: $\widehat{AOB}+\widehat{BOC}+\widehat{COD}+\widehat{DOE}+\widehat{EOG}+\widehat{GOH}+\widehat{HOK}+\widehat{KOA}=360°$

Suy ra $8\widehat{AOB}=360°,$ nên $\widehat{AOB}=45°.$

Do đó, $\widehat{DOE}=\widehat{EOG}=\widehat{GOH}=45°.$

Như vậy, ta sẽ có $\widehat{DOG}=\widehat{DOE}+\widehat{EOF}+\widehat{FOG}=45°+45°+45°=135°.$

Vậy quay thuận chiều 135° tâm O biến điểm D của bát giác đều ABCDEFGH thành điểm G.

Do đó ta chọn phương án A.

Bài 2. Phép quay giữ nguyên hình đa giác đều A₁A₂A₃...A_n (n ≥ 3, n ∈ ℕ) là

A. Phép quay có tâm là một đỉnh bất kì của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó;

B. Phép quay có tâm là tâm của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành tâm của hình đa giác đều đó;

C. Phép quay có tâm là tâm của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó;

D. Phép quay có tâm là một đỉnh bất kì của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành tâm của hình đa giác đều đó.

Hướng dẫn giải

Đáp án đúng là: C

Giả sử hình đa giác đều A₁A₂...A_n (n ≥ 3, n ∈ ℕ) có tâm O.

Phép quay giữ nguyên hình đa giác đều A₁A₂...A_n là phép quay tâm O biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó.

Do đó Vậy phép quay giữ nguyên hình đa giác đều A₁A₂A₃...A_n (n ≥ 3, n ∈ ℕ) là phép quay có tâm là tâm của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó.

Vậy ta chọn phương án C.

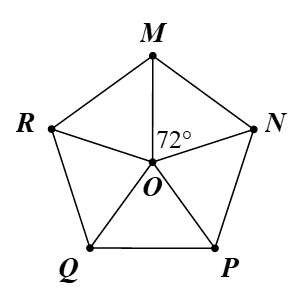
Bài 3. Cho ngũ giác đều MNPQR có tâm O. Phép quay nào với tâm O biến ngũ giác đều MNPQR thành chính nó?

A. 60°;

B. 72°;

C. 90°;

D. 120°.

Hướng dẫn giải

Đáp án đúng là: B

Các phép quay giữ nguyên ngũ giác đều MNPQR là:

⦁ Năm phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị:

${\alpha }_1^o=\frac{360°}{5}=72°;{\alpha }_2^o=\frac{2\cdot 360°}{5}=144°;{\alpha }_3^o=\frac{3\cdot 360°}{5}=216°;$

${\alpha }_4^o=\frac{4\cdot 360°}{5}=288°;{\alpha }_5^o=\frac{5\cdot 360°}{5}=360°.$

⦁ Ba phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị:

${\alpha }_1^o=\frac{360°}{5}=72°;{\alpha }_2^o=\frac{2\cdot 360°}{5}=144°;{\alpha }_3^o=\frac{3\cdot 360°}{5}=216°;$

${\alpha }_4^o=\frac{4\cdot 360°}{5}=288°;{\alpha }_5^o=\frac{5\cdot 360°}{5}=360°.$

Do đó ta chọn phương án B.

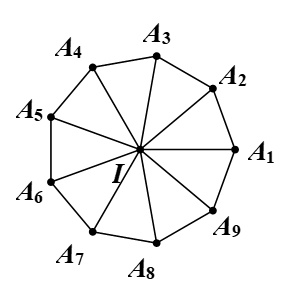
Bài 4. Cho hình đa giác đều có 9 cạnh A₁A₂A₃A₄A₅A₆A₇A₈A₉ tâm I.

a) Phép quay thuận chiều 40° tâm I biến các điểm A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉ thành các điểm nào? Phép quay này có giữ nguyên đa giác đều A₁A₂A₃A₄A₅A₆A₇A₈A₉ không?

b) Chỉ ra các phép quay giữ nguyên đa giác đều A₁A₂A₃A₄A₅A₆A₇A₈A₉.

Hướng dẫn giải

a) Do A₁A₂A₃A₄A₅A₆A₇A₈A₉ là đa giác đều nên A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ và OA₁ = OA₂ = OA₃ = OA₄ = OA₅ = OA₆ = OA₇ = OA₈ = OA₉.

Xét ∆OA₁A₂ và ∆OA₂A₃ có:

OA₁ = OA₂, OA₂ = OA₃, A₁A₂ = A₂A₃

Do đó ∆OA₁A₂= ∆OA₂A₃ (c.c.c).

Tương tự, ta sẽ chứng minh được:

∆OA₁A₂= ∆OA₂A₃ = ∆OA₃A₄ = ∆OA₄A₅ = ∆OA₅A₆ = ∆OA₆A₇ = ∆OA₇A₈ = ∆OA₈A₉ = ∆OA₉A₁.

Suy ra các góc tương ứng bằng nhau: $\widehat{A_{1}O{A}_2}=\widehat{A_{2}O{A}_3}=\widehat{A_{3}O{A}_4}=\widehat{A_{4}O{A}_5}=\widehat{A_{5}O{A}_6}=\widehat{A_{6}O{A}_7}=\widehat{A_{7}O{A}_8}=\widehat{A_{8}O{A}_9}=\widehat{A_{9}O{A}_1}.$

Ta có: $\widehat{A_{1}O{A}_2}+\widehat{A_{2}O{A}_3}+\widehat{A_{3}O{A}_4}+\widehat{A_{4}O{A}_5}+\widehat{A_{5}O{A}_6}+\widehat{A_{6}O{A}_7}+\widehat{A_{7}O{A}_8}+\widehat{A_{8}O{A}_9}+\widehat{A_{9}O{A}_1}=360°$

Suy ra $9\widehat{A_{1}O{A}_2}=360°,$ nên $\widehat{A_{1}O{A}_2}=40°.$

Vậy phép quay thuận chiều 40° tâm I biến các điểm A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉ theo thứ tự thành các điểm A₉, A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈.

Vì phép quay trên biến mỗi đỉnh của đa giác đều A₁A₂A₃A₄A₅A₆A₇A₈A₉ thành một đỉnh của đa giác đều đó nên phép quay trên giữ nguyên đa giác đều A₁A₂A₃A₄A₅A₆A₇A₈A₉.

b) Có 18 phép quay giữ nguyên đa giác đều A₁A₂A₃A₄A₅A₆A₇A₈A₉ là:

⦁ Chín phép quay thuận chiều α° tâm I với α° lần lượt nhận các giá trị 40°; 80°; 120°; 160°; 200°; 240°; 280°; 320°; 360°;

⦁ Chín phép quay ngược chiều α° tâm I với α° lần lượt nhận các giá trị 40°; 80°; 120°; 160°; 200°; 240°; 280°; 320°; 360°.

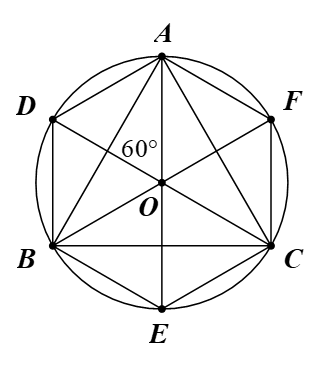
Bài 5. Cho tam giác đều ABC nội tiếp đường tròn (O). Phép quay ngược chiều 60° tâm O biến các điểm A, B, C theo thứ tự thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.

Hướng dẫn giải

⦁ Vì tam giác ABC đều nên $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60°.$

Xét đường tròn (O), có $\widehat{ACB},\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm chắn cung nhỏ AB nên $\widehat{ACB}=\frac{1}{2}\widehat{AOB}.$

Suy ra $\widehat{AOB}=2\cdot \widehat{ACB}=2\cdot 60°=120°.$

⦁ Vì phép quay ngược chiều 60° tâm O biến điểm A thành điểm D nằm trên đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OD thì điểm A tạo nên cung AD có số đo 60°.

Khi đó OA = OD và $\widehat{AOD}=60°.$ Vì vậy tam giác OAD đều.

Suy ra AD = OA = OD và $\widehat{ODA}=60°$ (1)

⦁ Mặt khác, $\widehat{AOB}=\widehat{AOD}+\widehat{BOD}$ (hai góc kề nhau).

Suy ra $\widehat{BOD}=\widehat{AOB}-\widehat{AOD}=120°-60°=60°.$

Xét ∆BOD, có: OB = OD (= OA) và $\widehat{BOD}=60°.$

Suy ra tam giác BOD đều.

Do đó BD = OB = OD và $\widehat{ODB}=60°$ (2)

Từ (1), (2), ta suy ra AD = BD và $\widehat{ADB}=\widehat{ODA}+\widehat{ODB}=60°+60°=120°.$

Tương tự như vậy, ta chứng minh được AD = DB = BE = EC = CF = FA và $\widehat{ADB}=\widehat{DBE}=\widehat{BEC}=\widehat{ECF}=\widehat{CFA}=\widehat{FAD}=120°.$

Vậy đa giác ADBECF có các cạnh bằng nhau và các góc đều bằng 120° nên đa giác ADBECF là lục giác đều.

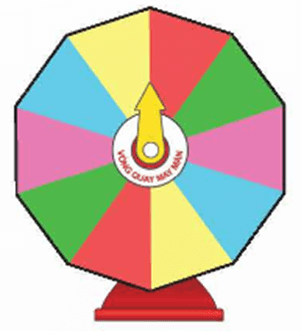
Bài 6. Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh như hình dưới đây.

Tìm các phép quay giữ nguyên đa giác đều đã cho.

Hướng dẫn giải

Gọi O là tâm của đa giác đều 10 cạnh đã cho.

Vì đa giác đều đã cho có 10 cạnh nên đa giác đều đó có 10 đỉnh.

Vậy có 20 phép quay giữ nguyên đa giác đều đã cho là:

⦁ Mười phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 36°; 72°; 108°; 144°; 180°; 216°; 252°; 288°; 324°; 360°;

⦁ Mười phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 36°; 72°; 108°; 144°; 180°; 216°; 252°; 288°; 324°; 360°.