Lý thuyết Hình trụ - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 1: Hình trụ

1. Hình trụ

1.1. Nhận biết hình trụ

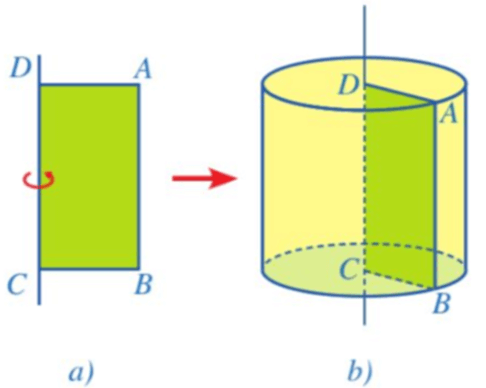
Cắt một miếng bìa có dạng hình chữ nhật ABCD. Khi quay miếng bìa một vòng quanh đường thẳng cố định chứa cạnh CD (Hình a), miếng bìa đó tạo nên một hình như ở Hình b.

Nhận xét: Hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh đường thẳng cố định chứa một cạnh của nó là hình trụ.

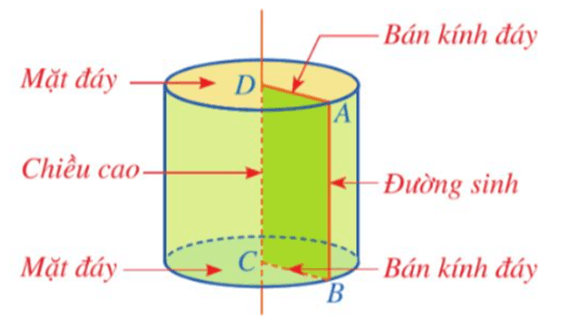
Với hình trụ như ở hình vẽ trên, ta có:

⦁ Hình tròn tâm D bán kính DA và hình tròn tâm C bán kính CB là hai mặt đáy; hai mặt đáy của hình trụ bằng nhau và nằm trong hai mặt phẳng song song;

⦁ Độ dài cạnh DA được gọi là bán kính đáy;

⦁ Độ dài cạnh CD được gọi là chiều cao;

⦁ Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh; độ dài đường sinh bằng chiều cao của hình trụ.

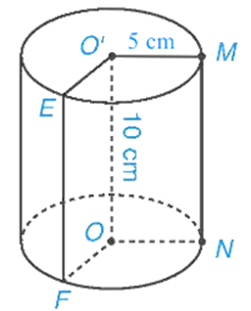
Ví dụ 1. Cho hình trụ ở hình bên.

a) Kể tên bốn bán kính đáy và hai đường sinh của hình trụ.

b) Cho biết độ dài bán kính đáy, chiều cao và độ dài đường sinh của hình trụ.

Hướng dẫn giải

a) O’M, O’E, ON, OF là bốn bán kính đáy của hình trụ.

MN, EF là hai đường sinh của hình trụ.

b) Độ dài bán kính đáy của hình trụ là: O’E = ON = OF = O’M = 5 cm.

Chiều cao của hình trụ là: OO’ = 10 cm.

Độ dài đường sinh của hình trụ là: MN = EF = OO’ = 10 cm.

1.2. Tạo lập hình trụ

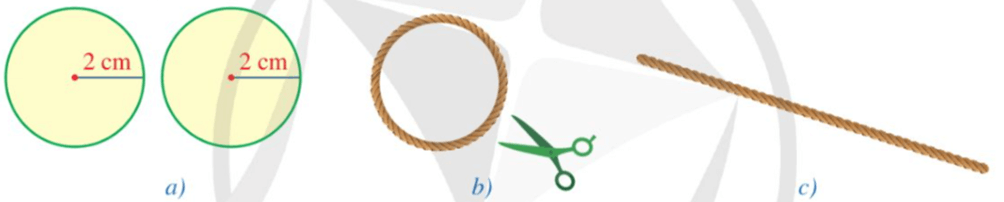
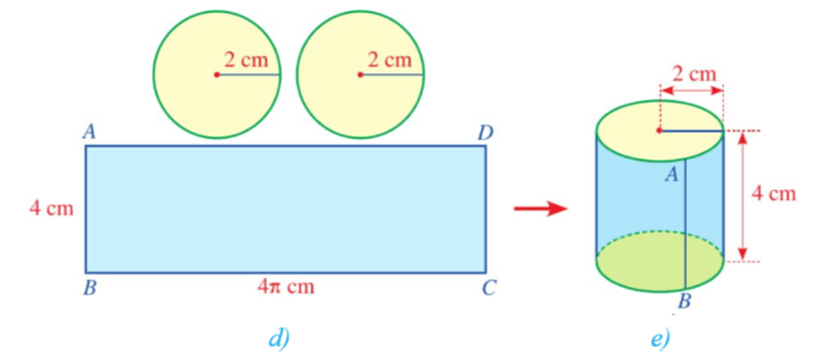
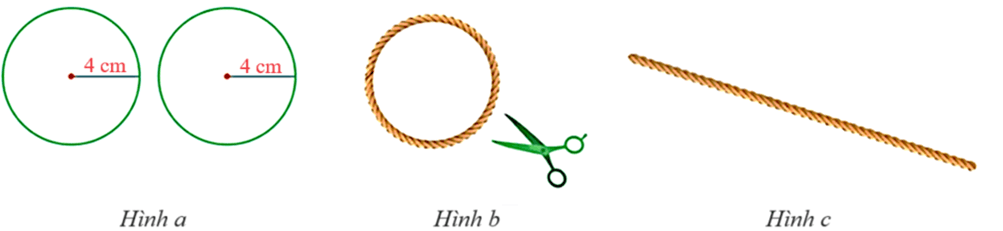
a) Cắt hai miếng bìa có dạng hình tròn với bán kính bằng 2 cm (Hình a).

b) Lấy một sợi dây dài mảnh không dãn và tạo vòng dây cuốn quanh (một vòng) miếng bìa tròn thứ nhất (Hình b), cắt vòng dây và kéo thẳng vòng dây đó để nhận được đoạn dây như ở Hình c.

Cắt một miếng bìa có dạng hình chữ nhật ABCD với chiều dài bằng độ dài đoạn dây ở Hình c và chiều rộng bằng 4 cm.

c) Ghép và dán các miếng bìa vừa cắt ở câu a, b (Hình d) để được một hình trụ như ở Hình e.

Ví dụ 2. Tạo lập một hình trụ có bán kính đáy là 4 cm và chiều cao là 5 cm.

Hướng dẫn giải:

Để tạo lập được một hình trụ có bán kính đáy là 4 cm, chiều cao là 5 cm, ta làm như sau:

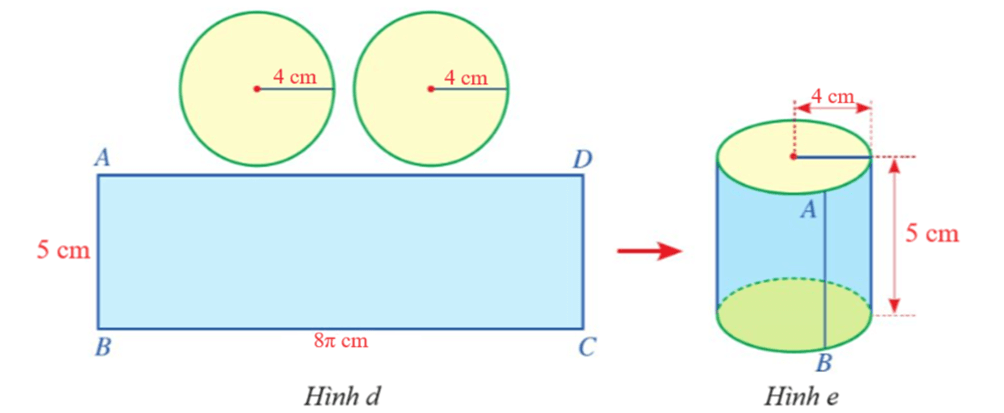
Bước 1. Cắt hai miếng bìa có dạng hình tròn với bán kính bằng 4 cm (Hình a).

Bước 2. Lấy một sợi dây dài mảnh không dãn và tạo vòng dây cuốn quanh (một vòng) miếng bìa tròn thứ nhất (Hình b), cắt vòng dây và kéo thẳng vòng dây đó để nhận được đoạn dây như ở Hình c.

Bước 3. Cắt một miếng bìa có dạng hình chữ nhật ABCD với chiều dài bằng độ dài đoạn dây ở Hình c và chiều rộng bằng 5 cm.

Bước 4. Ghép và dán các miếng bìa vừa cắt ở Bước 1, Bước 3 (Hình d) để được một hình trụ như ở Hình e.

2. Diện tích xung quanh của hình trụ

Diện tích xung quanh của hình trụ bằng tích của chu vi đáy với chiều cao:

S_xq = C.h = 2πrh,

trong đó S_xq là diện tích xung quanh, C là chu vi đáy, r là bán kính đáy, h là chiều cao của hình trụ.

Chú ý: Tổng của diện tích xung quanh và diện tích hai đáy của hình trụ gọi là diện tích toàn phần của hình trụ.

Diện tích toàn phần S_tp của hình trụ được tính theo công thức:

S_tp = 2πrh + 2πr² = 2πr(h + r),

trong đó r là bán kính đáy và h là chiều cao của hình trụ.

Ví dụ3. Cho một hình trụ có bán kính đáy là 5 cm và chiều cao là 16 cm.

a) Tính diện tích xung quanh của hình trụ.

b) Tính diện tích toàn phần của hình trụ.

Hướng dẫn giải

a) Diện tích xung quanh của hình trụ là:

S_xq = 2πrh = 2π.5.16 = 160π (cm²).

b) Diện tích toàn phần của hình trụ là:

S_tp = 2πr(h + r) = 2π.5.(16 + 5) = 210π (cm²).

3. Thể tích của hình trụ

Thể tích của hình trụ bằng tích của diện tích đáy với chiều cao:

V = S.h = πr²h,

trong đó V là thể tích, S là diện tích đáy, r là bán kính đáy, h là chiều cao của hình trụ.

Ví dụ4. Tính thể tích của hình trụ có bán kính đáy là 7 dm, chiều cao là 12 dm.

Hướng dẫn giải

Thể tích của hình trụ là:

V = πr²h = π.7².12 = 588π (dm³).

Bài tập Hình trụ

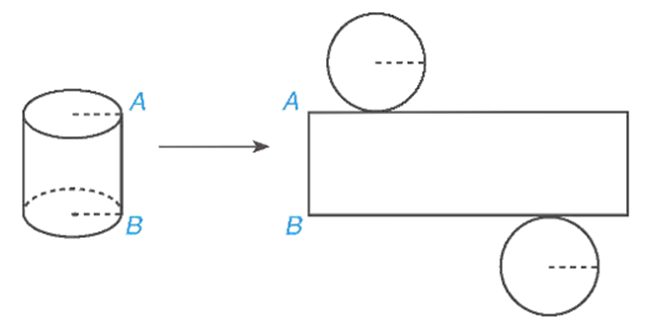
Bài 1. Từ một hình trụ, khi ta cắt rời hai đáy và cắt theo một đường sinh nào đó rồi trải phẳng ra thì ta được một hình phẳng gồm:

A. Một hình tròn và một hình chữ nhật;

B. Hai hình tròn và hai hình vuông;

C. Hai hình tròn và một hình chữ nhật;

D. Hai hình tứ giác và một hình chữ nhật.

Hướng dẫn giải

Đáp án đúng là: C

Từ một hình trụ, khi ta cắt rời hai đáy và cắt theo một đường sinh nào đó rồi trải phẳng ra thì ta được một hình phẳng gồm hai hình tròn và một hình chữ nhật.

Vậy ta chọn phương án C.

Bài 2. Điền vào chỗ trống: “Hình trụ được tạo ra khi quay một ... một vòng xung quanh đường thẳng cố định chứa một cạnh của nó.”

A. Hình tam giác;

B. Hình chữ nhật;

C. Hình bình hành;

D. Hình tròn.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: “Hình trụ được tạo ra khi quay một hình chữ nhật một vòng xung quanh đường thẳng cố định chứa một cạnh của nó.”

Vậy ta chọn phương án B.

Bài 3. Diện tích xung quanh của hình trụ có đường kính đáy 18 m và chiều cao 6 m bằng

A. 108π cm²;

B. 486π m³;

C. 54π m²;

D. 108π m².

Hướng dẫn giải

Đáp án đúng là: D

Bán kính đáy của hình trụ là: r = 18 : 2 = 9 (m).

Diện tích xung quanh của hình trụ là: S_xq = 2πrh = 2π.9.6 = 108π (m²).

Do đó ta chọn phương án D.

Bài 4. Một hình trụ có bán kính đáy là 20 cm và chiều cao gấp 3 lần đường kính đáy. Tính:

a) Diện tích xung quanh của hình trụ.

b) Diện tích toàn phần của hình trụ.

c) Thể tích của hình trụ.

Hướng dẫn giải

a) Đường kính đáy của hình trụ là: 20.2 = 40 (cm).

Chiều cao của hình trụ là: 3.40 = 120 (cm).

Diện tích xung quanh của hình trụ là:

S_xq = 2πrh = 2π.20.120 = 4800π (cm²).

b) Diện tích toàn phần của hình trụ là:

S_tp = 2πr(h + r) = 2π.20.(120 + 20) = 5600π (cm²).

c) Thể tích của hình trụ là:

V = πr²h = π.20².120 = 48 000π (cm³).

Bài 5. Một nhà máy dự định sản xuất thùng phuy đựng dầu nhớt dạng hình trụ có bán kính đáy 0,4 m và chiều cao 1,5 m (hình vẽ).

a) Bỏ qua diện tích các mép thùng, hãy tính diện tích thép cần dùng để sản xuất 200 thùng phuy như vậy (kết quả làm tròn đến hàng phần trăm).

b) Nếu cần đựng 5 000 lít dầu thì cần sử dụng ít nhất bao nhiêu thùng phuy như vậy?

Hướng dẫn giải

a) Diện tích toàn phần của một thùng phuy là:

S_tp = 2πr(h + r) = 2π.0,4.(1,5 + 0,4) = 1,52π (m²).

Diện tích thép cần dùng để sản xuất 200 thùng phuy là:

1,52π.200 = 304π (m²).

b) Thể tích của một thùng phuy là:

V = πr²h = π.0,4².1,5 = 0,24π (m³).

Đổi đơn vị: 0,24π m³ = 240π lít.

Ta có: 5 000 : (240π) ≈ 6,63.

Vậy nếu cần đựng 5 000 lít dầu thì cần sử dụng ít nhất 7 thùng phuy như vậy.

Bài 6. Phần bên trong của một cái bể hình trụ có chiều cao 1,8 m và chu vi đáy là 2,6π m. Tính thể tích lượng nước có trong bể biết mực nước bằng $\frac{4}{5}$ chiều cao của bể (kết quả làm tròn đến hàng phần mười).

Hướng dẫn giải

Bán kính của phần bên trong bể nước là:$r=\frac{2,6\pi }{2\pi }=1,3$ (m).

Thể tích của phần bên trong bể nước là:

V = πr²h = π.1,3².1,8 = 3,042π (m³).

Thể tích lượng nước có trong bể là:

$\frac{4}{5}.3,042\pi =2,4336\pi \approx 7,6$ (m³).

Vậy thể tích lượng nước có trong bể khoảng 7,6 m³.