Lý thuyết Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Toán 9 Cánh diều

Lý thuyết Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

1. Đường tròn ngoại tiếp tam giác

1.1. Định nghĩa

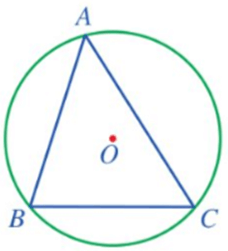
– Định nghĩa: Đường tròn đi qua ba đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác đó.

Chú ý: Khi đường tròn (O) ngoại tiếp tam giác ABC, ta còn nói tam giác ABC nội tiếp đường tròn (O).

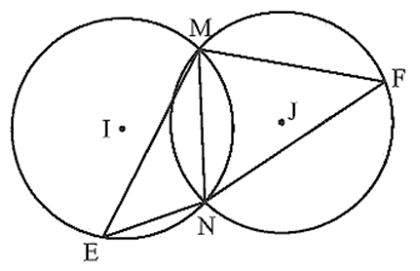
Ví dụ 1. Cho hai đường tròn (I) và (J) cắt nhau tại M và N. Gọi E, F lần lượt là hai điểm trên đường tròn (I) và (J) (E, F ≠ M, N).

a) Đường tròn nào ngoại tiếp tam giác MNE?

b) Tam giác MNF nội tiếp đường tròn nào?

Hướng dẫn giải

a) Đường tròn (I) là đường tròn ngoại tiếp tam giác MNE vì đường tròn (I) đi qua cả ba đỉnh M, N, E của tam giác MNE.

b) Tam giác MNF nội tiếp đường tròn (J) vì đường tròn (J) đi qua cả ba đỉnh M, N, F của tam giác MNF.

1.2. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác

– Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó.Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác đó.

Nhận xét:

⦁ Vì ba đường trung trực của tam giác cùng đi qua một điểm nên tâm đường tròn ngoại tiếp tam giác là giao điểm hai đường trung trực bất kì của tam giác đó.

⦁ Mỗi tam giác có đúng một đường tròn ngoại tiếp.

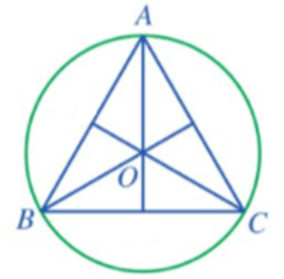
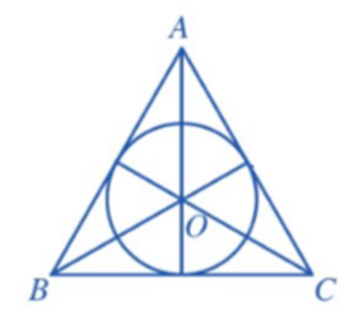
Chẳng hạn, ở hình vẽ dưới đây, ta có:

Ba đường trung trực ứng với mỗi cạnh AB, BC, CA của tam giác ABC cắt nhau tại O.

Khi đó O là tâm của đường tròn ngoại tiếp tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC là R = OA = OB = OC.

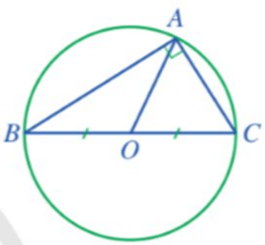
– Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng nửa cạnh huyền của tam giác vuông đó.

Ví dụ 2. Cho tam giác ABC vuông tại A có AB = 8 cm và AC = 6 cm. Xác định tâm và tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải

Gọi O là trung điểm của BC.

Vì tam giác ABC vuông tại A nên O là tâm của đường tròn ngoại tiếp tam giác ABC.

Tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC²

Suy ra BC² = 8² + 6² = 100.

Do đó $BC=\sqrt{100}=10$ (cm)

Vì tam giác ABC vuông tại A nên bán kính R của đường tròn ngoại tiếp tam giác ABC bằng nửa cạnh huyền BC.

Do đó $R=\frac{BC}{2}=\frac{10}{2}=5$(cm).

Vậy đường tròn ngoại tiếp tam giác ABC có tâm O là trung điểm của BC và bán kính R = 5 cm.

–Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn ngoại tiếp của tam giác đó.Tam giác đều cạnh a có bán kính đường tròn ngoại tiếp là $R=\frac{a\sqrt{3}}{3}.$

Ví dụ 3.Xác định tâm và tính bán kính của đường tròn ngoại tiếp tam giác đều ABC có cạnh bằng 9 cm.

Hướng dẫn giải

Gọi O là trọng tâm của tam giác ABC.Khi đó O là tâm đường tròn ngoại tiếp tam giác đều ABC.

Bán kính của đường tròn ngoại tiếp tam giác đều ABC là:

$R=\frac{9\cdot \sqrt{3}}{3}=3\sqrt{3}$(cm).

Vậy đường tròn ngoại tiếp tam giác đều ABC có tâm O là trọng tâm của tam giác ABC và bán kính $R=3\sqrt{3}$cm.

2. Đường tròn nội tiếp tam giác

2.1. Định nghĩa

– Định nghĩa: Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác đó.

Chú ý: Khi đường tròn (I) nội tiếp tam giác ABC, ta còn nói tam giác ABC ngoại tiếp đường tròn (I).

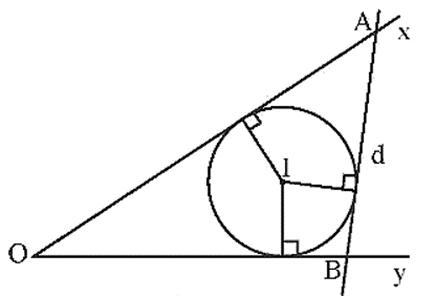
Ví dụ 4.Cho $\widehat{xOy}$và đường tròn (I) tiếp xúc với hai cạnh Ox, Oy. Kẻ tiếp tuyến d của đường tròn (I) sao cho d cắt Ox, Oy lần lượt tại A, B và I nằm trong tam giác OAB.

Khi đó đường tròn (I) nội tiếp tam giác OAB hay tam giác OAB ngoại tiếp đường tròn (I).

2.2. Xác định tâm và bán kính đường tròn nội tiếp tam giác

– Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác đó. Bán kính đường tròn nội tiếp tam giác bằng khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó.

Nhận xét:

⦁ Vì ba đường phân giác của một tam giác cùng đi qua một điểm nên tâm đường tròn nội tiếp là giao điểm hai đường phân giác bất kì của tam giác đó.

⦁ Mỗi tam giác có đúng một đường tròn nội tiếp.

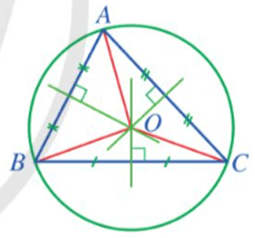
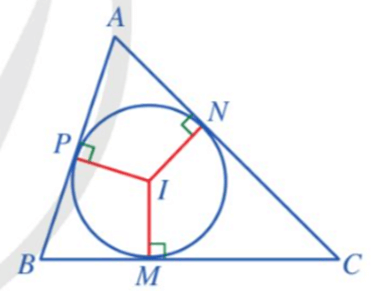
Chẳng hạn, ở hình vẽ dưới đây, ta có:

Ba đường phân giác xuất phát từ các đỉnh A, B, C của tam giác ABC cắt nhau tại I.

Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.

Khi đó I là tâm của đường tròn nội tiếp tam giác ABC và bán kính đường tròn nội tiếp tam giác ABC là r = IM = IN = IP.

– Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn nội tiếp tam giác đó. Tam giác đều cạnh a có bán kính đường tròn nội tiếp là $r=\frac{a\sqrt{3}}{6}.$

Ví dụ 5. Xác định tâm và tính bán kính của đường tròn ngoại tiếp tam giác đều ABC có cạnh bằng 12 cm.

Hướng dẫn giải

Gọi O là trọng tâm của tam giác ABC.Khi đó O là tâm đường tròn nội tiếp tam giác đều ABC.

Bán kính của đường tròn nội tiếp tam giác đều ABC là:

$r=\frac{a\sqrt{3}}{6}=\frac{12.\sqrt{3}}{6}=2\sqrt{3}$(cm).

Vậy đường tròn nội tiếp tam giác đều ABC có tâm O là trọng tâm của tam giác ABC và bán kính $r=2\sqrt{3}$cm.

Bài tập Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Bài 1. Khẳng định nào sau đây là sai?

A. Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó;

B. Tâm đường tròn nội tiếp tam giác là giao điểm ba đường trung tuyến của tam giác đó;

C. Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác đó;

D. Bán kính của đường tròn ngoại tiếp tam giác vuông bằng nửa độ dài cạnh huyền của tam giác vuông đó.

Hướng dẫn giải

Đáp án đúng là: B

Phương án A, C, D đúng.

Phương án B sai. Sửa lại: Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác đó.

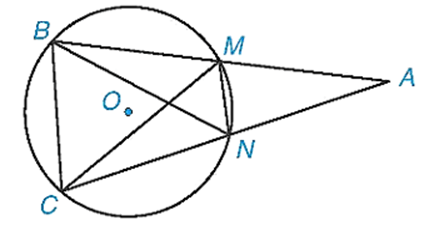
Bài 2. Có bao nhiêu tam giác nội tiếp đường tròn (O) ở hình vẽ dưới đây.

A. 2;

B. 3;

C. 4;

D. 5.

Hướng dẫn giải

Đáp án đúng là: C

Vì đường tròn (O) đi qua các điểm B, C, M, N nên đường tròn (O) ngoại tiếp các tam giác BCM, BCN, BMN, CMN.

Ta còn nói các tam giác BCM, BCN, BMN, CMN nội tiếp đường tròn (O).

Vậy có 4 tam giác nội tiếp đường tròn (O).

Bài 3. Cho tam giác MNP đều cạnh bằng $\sqrt{3}$ dm. Khi đó bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác đều MNP lần lượt bằng

A. 1 dm và 1 dm;

B. 0,5 dm và 0,5 dm;

C. 0,5 dm và 1 dm;

D. 1 dm và 0,5dm.

Hướng dẫn giải

Đáp án đúng là: D

Bán kính R của đường tròn ngoại tiếp tam giác đều MNP là:

$R=\frac{a\sqrt{3}}{3}=\frac{\sqrt{3}\cdot \sqrt{3}}{3}=1$ (dm).

Bán kính r của đường tròn nội tiếp tam giác đều MNP là:

$r=\frac{a\sqrt{3}}{6}=\frac{\sqrt{3}\cdot \sqrt{3}}{6}=\frac{1}{2}=0,5$ (dm).

Do đó ta chọn phương án D.

Bài 4. Cho tam giác ABC (AC < BC) nội tiếp đường tròn (O; R) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại điểm I (điểm I thuộc cung nhỏ CB).

a) Chứng minh rằng OI ⊥ BC.

b) Vẽ tiếp tuyến của đường tròn (O) tại B, cắt đường thẳng OI tại M. Chứng minh rằng MC là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

a) Đường tròn (O) có AB là đường kính, suy ra $\widehat{ACB}=90°$ (góc nội tiếp chắn nửa đường tròn là góc vuông)

Do đó AC ⊥ BC, mà OI // AC nên OI ⊥ BC.

b) Vì MB là tiếp tuyến của (O), với B là tiếp điểm nên MB ⊥ OB tại B hay $\widehat{OBM}=90°.$

Tam giác OBC cân tại O (OB = OC = R) có OI là đường cao nên cũng đồng thời là đường phân giác của tam giác OBC.Do đó $\widehat{BOI}=\widehat{COI}.$

Xét ∆BOM và ∆COM, có:

OM là cạnh chung;

OB = OC (= R);

$\widehat{BOM}=\widehat{COM}$ (chứng minh trên).

Do đó ∆BOM = ∆COM (c.g.c).

Suy ra $\widehat{OCM}=\widehat{OBM}=90°.$

Khi đó OC ⊥ MC tại điểm C nằm trên đường tròn (O).

Vậy MC là tiếp tuyến của đường tròn (O), với C là tiếp điểm.

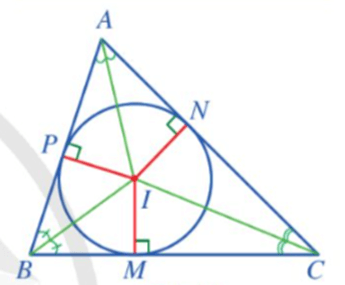
Bài 5. Cho đường tròn (I) nội tiếp tam giác ABC. Biết $\hat{A}=50°;\hat{B}=80°.$

a) Tính số đo của $\widehat{BIC},\widehat{CIA},\widehat{AIB}.$

b) Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, CA. Chứng minh rằng 2AD = AB + AC – BC.

Hướng dẫn giải

a) Tam giác ABC, có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{ACB}=180°-\left(\widehat{BAC}+\widehat{ABC}\right)=180°-\left(50°+80°\right)=50°.$

Vì đường tròn (I) nội tiếp tam giác ABC nên I là giao điểm ba đường phân giác của tam giác ABC.

Khi đó ta có:

⦁$\widehat{CAI}=\widehat{BAI}=\frac{\widehat{BAC}}{2}=\frac{50°}{2}=25°;$

⦁$\widehat{CBI}=\widehat{ABI}=\frac{\widehat{ABC}}{2}=\frac{80°}{2}=40°;$

⦁$\widehat{ACI}=\widehat{BCI}=\frac{\widehat{ACB}}{2}=\frac{50°}{2}=25°.$

Tam giác BIC, có: $\widehat{BIC}+\widehat{CBI}+\widehat{BCI}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{BIC}=180°-\left(\widehat{CBI}+\widehat{BCI}\right)=180°-\left(40°+25°\right)=115°.$

Tương tự, ta có: $\widehat{CIA}=130°$ và $\widehat{AIB}=115°.$

Vậy $\widehat{BIC}=115°;\widehat{CIA}=130°;\widehat{AIB}=115°.$

b) Ta có AF, AD là hai tiếp tuyến của (I) cắt nhau tại A nên AF = AD (tính chất hai tiếp tuyến cắt nhau)

Chứng minh tương tự, ta được BD = BE và CF = CE.

Ta có: AB + AC – BC = AD + DB + AF + FC – BC

= AD + BE + AD + CE – BC

= 2AD + (BE + CE) – BC

= 2AD + BC – BC

= 2AD.

Vậy 2AD = AB + AC – BC.

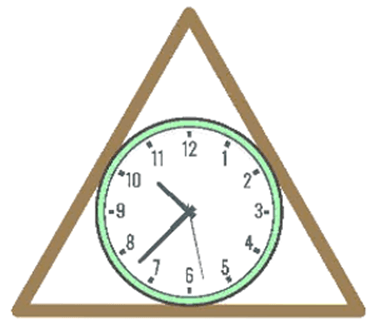
Bài 6. Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 40 cm. Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Hướng dẫn giải

Bán kính của chiếc đồng hồ hình tròn là: $r=\frac{40}{2}=20$ (cm).

Gọi a (cm) là độ dài cạnh (phía bên trong) của khung gỗ.

Ta có $r=\frac{a\sqrt{3}}{6},$hay $\frac{a\sqrt{3}}{6}=20,$ suy ra $a=40\sqrt{3}\approx 69,28$ (cm).

Vậy độ dài các cạnh (phía bên trong) của khung gỗ phải bằng khoảng 69,28 cm.