Nội dung bài viết

    Xem thêm

    Lý thuyết Một số phép tính về căn bậc hai của số thực - Toán 9 Cánh diều

    Tóm tắt lý thuyết Toán lớp 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 9.

    1 98 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực

    1. Căn bậc hai của một bình phương

    Quy tắc: Với mọi số a, ta có a2=a.

    Ví dụ 1.Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:

    a) 232;

    b) 3−102.

    Hướng dẫn giải

    a) 232=23=23;

    b) 3−102=3−10

    Do 9<10 hay 3<10 nên 3−10<0

    Vì thế ta có 3−10=10−3

    Vậy 3−102=3−10=10−3.

    2. Căn bậc hai của một tích

    Quy tắc: Với hai số không âm a và b, ta có a⋅b=a⋅b.

    Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.

    Ví dụ 2.Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:

    a) 36⋅1,44

    b) −27⋅48.

    Hướng dẫn giải

    a) 36⋅1,44=36⋅1,44=6⋅1,2=7,2;

    b) −27⋅48=−27⋅48=−1296=−36.

    3. Căn bậc hai của một thương

    Quy tắc: Với a ≥ 0 và b > 0, ta có ab=ab.

    Ví dụ 3.Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:

    a) 28936;

    b) 1473.

    Hướng dẫn giải

    a) 28936=28936=176;

    b)1473=1473=49=7.

    4. Đưa thừa số ra ngoài dấu căn bậc hai

    Quy tắc: Cho hai số a, b với b ≥ 0. Khi đó a2⋅b=ab.

    Cụ thể, ta có:

    ⦁Nếu a ≥ 0 và b ≥ 0 thì a2b=ab;

    ⦁Nếu a < 0 và b ≥ 0 thì a2b=-ab;

    Ví dụ 4.Rút gọn biểu thức sau: 50+18−22.

    Hướng dẫn giải

    Ta có: 50+18−22=25⋅2+9⋅2−22

    =52⋅2+32⋅2−22=52+32−22=62.

    5. Đưa thừa số vào trong dấu căn bậc hai

    Quy tắc:

    ⦁ Với a ≥ 0 và b ≥ 0 thì ab=a2b;

    ⦁ Nếu a < 0 và b ≥ 0 thì ab=-a2b;

    a) 212;

    b) 525−210.

    Hướng dẫn giải

    a) 212=22⋅12=2;

    b) 525−210=52⋅25−210=10−210=−10.

    Sơ đồ tư duy Một số phép tính về căn bậc hai của số thực

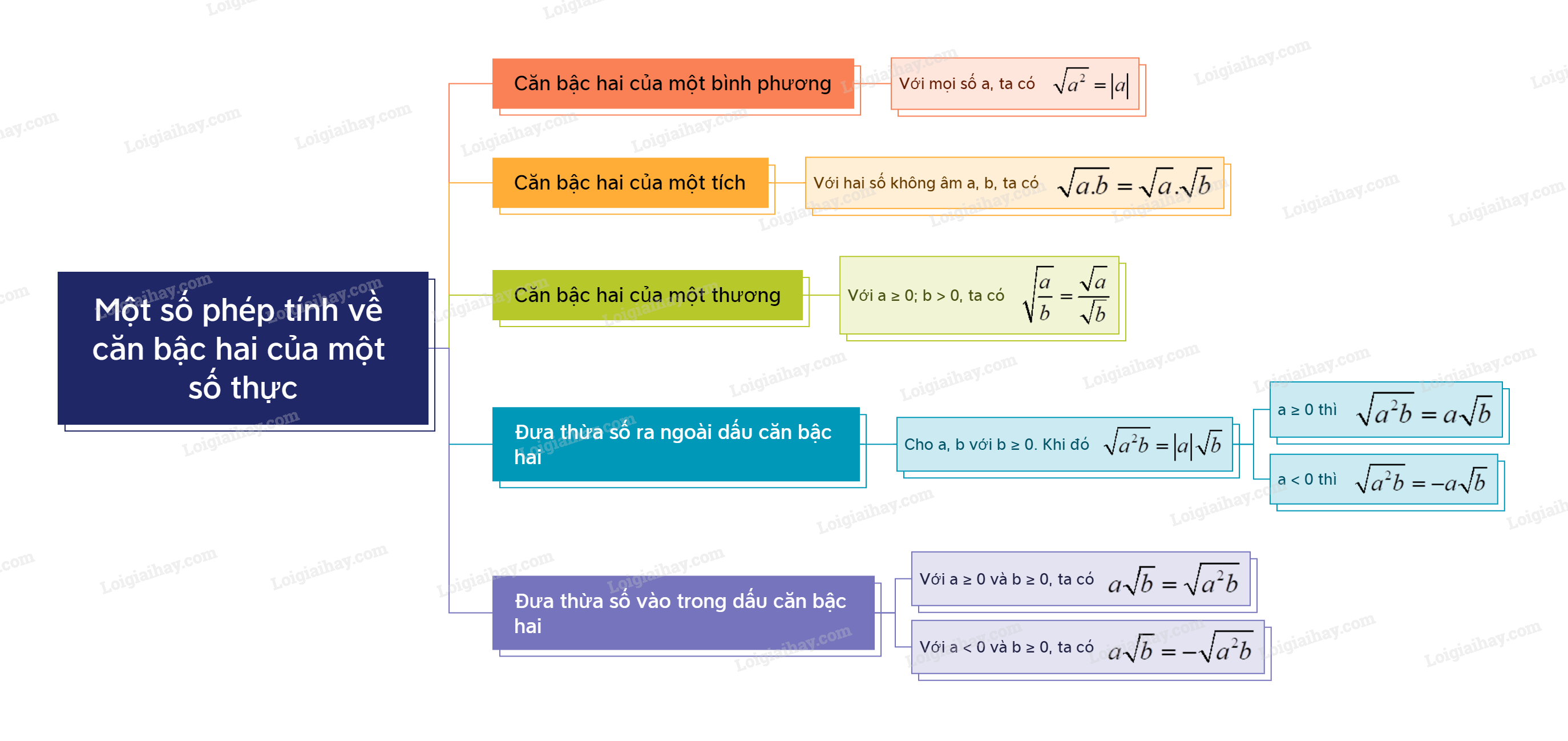
    Lý thuyết Một số phép tính về căn bậc hai của số thực - Toán 9 Cánh diều (ảnh 1)

    Bài tập Một số phép tính về căn bậc hai của số thực

    Bài 1.Cho a và b là hai số. Khẳng định nào sau đây là đúng?

    A. ab=a2b với mọi a, b;

    B. a2=−a khi a < 0;

    C. ab2=−ba khi a ≥ 0 và b ≥ 0;

    D. −ab=−a⋅b khi a ≥ 0 và b ≥ 0.

    Hướng dẫn giải

    Đáp án đúng là: B

    Ta có:

    ⦁ a2=−a khi a < 0;

    ⦁ ab=a2b khi a ≥ 0 và b ≥ 0;

    ⦁ ab2=−ba khi a ≥ 0 và b < 0;

    ⦁ −ab=−a⋅b khi a < 0 và b ≥ 0 hoặc −ab=a⋅−b khi a ≥ 0 và b < 0.

    Vậy ta chọn phương án B.

    Bài 2. Cho a, b là hai số và b ≠ 0. Rút gọn biểu thức ta được

    A. a2b;

    B. ab;

    C. −a2b;

    D. a2b.

    Hướng dẫn giải

    Đáp án đúng là: D

    Ta có: a4b2=a2b2=a2b=a2b.

    Bài 3. Cho ba số dương a, b, c. Khẳng định nào sau đây là đúng?

    A. abc=abcb;

    B. abc=−abcbc;

    C. abc=abcbc;

    D. abc=abcbc.

    Hướng dẫn giải

    Đáp án đúng là: C

    Với a > 0, b > 0, c > 0, ta có:

    abc=abcbc2=abcbc2=abcbc=abcbc.

    Vậy ta chọn phương án C.

    Bài 4. So sánh:

    a) 497 và 3;

    b) 12.92 và 32;

    c) 50 và 55

    Hướng dẫn giải

    a) Ta có: 497=497=7

    Vì 7<9hay 7<3 nên 497<3.

    b) Ta có: 12⋅92=12⋅92=94=32.

    c) Ta có: 50=25⋅2=52⋅2=52.

    Vì 2<5 nên 52<55.

    Vậy 50<55.

    Bài 5. Tính:

    a) 7−43;

    b) 5+3⋅3−5;

    c) 6,22−5,922,43;

    d) 6−52+120.

    Hướng dẫn giải

    a) 7−43=4−2⋅2⋅3+3=22−2⋅2⋅3+32

    =2−32=2−3=2−3 (vì 2−3>0 > do 2>3).

    /span>

    b)5+3⋅3−5=3+53−5

    =32−52=9−5=4=2.

    c) 6,22−5,922,43=6,2−5,9⋅6,2+5,92,43

    =0,3⋅12,12,43=3,632,43=3,632,43=363243=12181=119.

    d) 6−52+120=6−26⋅5+5+4⋅30

    =11−26⋅5+22⋅30=11−230+230=11.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 98 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: