Trắc nghiệm Ôn tập chương 6 (có đáp án)
Trắc nghiệm Toán 10 Ôn tập chương 6
-
670 lượt thi
-
23 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Vì trục (l) đi qua đỉnh và tâm của hình vuông nên trục (l)≡OA nên số đo của các góc giữa tia OA với trục (l) bằng 0o+ k360o=k360o.
Câu 2:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Độ dài của cung π2rad=90o trên đường tròn được tính bằng công thức:
π. ao180.R=π180.90.10π=5 cm
Câu 3:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Độ dài của cung trên đường tròn được tính bằng công thức:
Câu 5:
10/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải.
Hay A= sin α - sinα = 0.
*Phương pháp giải:
Sử dụng công thức chu kì và hai góc phụ nhau, bù nhaun để tính giá trị của biểu thức.
*Lý thuyết:
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = - cos α;
tan (180° – α) = - tan α (α ≠ 90°);
cot (180° – α) = - cot α (0° < α < 180°).
Chú ý:
- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.
Xem thêm
Câu 6:
10/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải.
*Phương pháp giải:
Sử dụng công thức chu kì và hai góc phụ nhau, bù nhaun để tính giá trị của biểu thức.
*Lý thuyết:
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = - cos α;
tan (180° – α) = - tan α (α ≠ 90°);
cot (180° – α) = - cot α (0° < α < 180°).
Chú ý:
- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.
Xem thêm
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Theo công thức đổi đơn vị độ sang radial ta có số đo độ của góc là
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Theo công thức đổi đơn vị số đo radian của góc là
Câu 14:
23/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải
Theo công thức đổi đơn vị, ta có số đo cung đã cho có số đo bằng radial, với
*Phương pháp giải:
* Đổi độ sang rađian:
Áp dụng lý thuyết: , ta suy ra: .
* Đổi rađian sang độ:
Áp dụng lý thuyết: , ta suy ra
Chú ý: Khi viết số đo của một góc (hay cung) theo đơn vị rađian, người ta thường không viết chữ rad sau số đo.
*Lý thuyết:
a. Đơn vị đo góc và cung tròn, độ dài cung tròn:
* Đơn vị rađian: Cung tròn có độ dài bằng bán kính gọi là cung có số đo 1 rađian, gọi tắt là cung 1 rađian. 1 rađian còn viết tắt là 1 rad.
Vì tính thông dụng của đơn vị rađian người ta thường không viết rađian hay rad sau số đo của cung và góc.
* Độ dài cung tròn. Quan hệ giữa độ và rađian:
suy ra và
* Độ dài cung tròn
Một cung của đường tròn bán kính R có số đo thì độ dài .
b. Góc và cung lượng giác:
* Đường tròn định hướng: Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại gọi là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ gọi là chiều dương (cùng chiều kim đồng hồ là chiều âm).
* Góc, cung lượng giác và số đo của chúng.
Cho đường tròn định hướng tâm O và hai tia Ou, Ov lần lượt cắt đường tròn tại U và V. Tia Om cắt đường tròn tại M, tia Om chuyển động theo một chiều (âm hoặc dương) quay quanh O khi đó điểm M cũng chuyển động theo một chiều trên đường tròn.
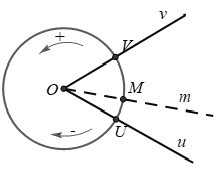
- Góc lượng giác: Tia Om quay xung quanh gốc O từ vị trí Ou đến vị trí Ov. Ta nói tia O đã tạo ra một góc lượng giác có tia đầu là Ou, tia cuối là Ov. Kí hiệu (Ou, Ov)
- Cung lượng giác: Điểm M chuyển động theo một chiều từ điểm U đến trùng với điểm V thì ta nói điểm M đã vạch nên một cung lượng giác có điểm đầu U, điểm cuối V. Kí hiệu là
- Số đo cung lượng giác:
+) Số đo của một cung lượng giác ( ) là một số thực, âm hay dương. Kí hiệu số đo của cung là sđ
+) Nếu một cung lượng giác có số đo ( hay ) thì mọi góc lượng giác cùng tia đầu, tia cuối với nó có số đo dạng (hay ) với .
+) Số đo của góc lượng giác (OU, OV) là số đo của cung lượng giác tương ứng
c. Biểu diễn cung lượng giác trên đường tròn lượng giác:
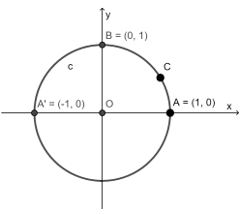
Đường tròn lượng giác là đường tròn định hướng có tâm O bán kính R = 1 trong hệ tọa độ Oxy. Ta lấy điểm A(1; 0) là điểm gốc của đường tròn đó.
Để biểu diễn cung lượng giác có số đo bằng trên đường tròn lượng giác, ta chọn điểm gốc là điểm A(1;0) và điểm ngọn C sao cho sđ .
Xem thêm
Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhấtCâu 15:
13/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Phương pháp giải:
- Sử dụng công thức tính độ dài cung tròn để tính
*Lời giải:
Theo công thức tính độ dài cung ta có độ dài cung có số đo 3,85rad là
. Làm tròn kết quả lên ta được D
*Một số dạng bài/lý thuyết nắm thêm về cách tính độ dài cung tròn:
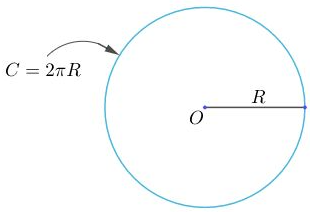
1_ Công thức tính độ dài đường tròn ( chu vi đường tròn )
Độ dài (C) của một đườn tròn bán kính R được tính theo công thức:
C=2πR hoặc C=πd (với d = 2R)
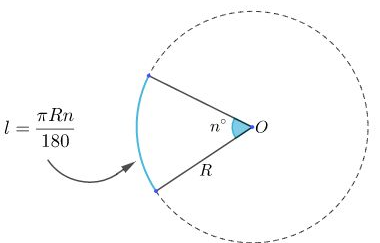
2_Công thức tính độ dài cung tròn
Trên đường tròn bán kính R, độ dài l của một cung n°được tính theo công thức
l=πRn180
3_Dạng bài toán:
a) Dạng 1: Tính độ dài đường tròn, cung tròn và các đại lượng liên quan
* Phương pháp giải: Áp dụng công thức đã nếu trong phần lí thuyết.
b) Dạng 2: Tính độ dài cung tròn do các cung chắp nối thành
* Phương pháp giải:Chia độ dài cung tròn mình cần tính thành các cung tròn nhỏ hơn của đường tròn khác sau đó sử dụng công thức tính độ dài cung tròn.
c) Dạng 3: So sánh độ dài các cung
* Phương pháp giải:
- Tính độ dài cung theo bán kính R và số đo của cung
- Sau khi thu được kết quả ta tiến hành so sánh.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
Ta có:
A đúng.
B đúng.
C đúng.
D sai.
Câu 17:
09/10/2024Biểu thức có giá trị bằng :
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Phương pháp giải:
- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc công, nhân lượng giác,... để thực hiên phép tính
*Lời giải:
*Các lý thuyết cần nằm về lượng giác
a. Công thức cộng:
b. Công thức nhân đôi, hạ bậc:
* Công thức nhân đôi:
* Công thức hạ bậc:
* Công thức nhân ba:
c. Công thức biến đổi tích thành tổng:
d. Công thức biển đổi tổng thành tích:
|
|
|
*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản
Câu 18:
16/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Phương pháp giải:
- Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi trong lượng giác để biến đổi thực hiện phép tính
*Lời giải:
Ta có:
Ta có
.
*Lý thuyết và các dạng bài tập về phép biến đổi lượng giác cần nắm:
+) Công thức biến đổi tổng thành tích
+) Công thức nhân đôi
Suy ra, công thức hạ bậc:
Dạng bài tập:
Dạng 1:
Phương pháp giải:
- Sử dụng định nghĩa giá trị lượng giá của một góc.
- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
- Sử dụng các công thức lượng giác.
Dạng 2: Chứng minh đẳng thức lượng giác
Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Thu gọn biểu thức lượng giác
Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn
Dạng 4: Chứng minh biểu thức không phụ thuộc vào biến
Phương pháp giải:
Chứng minh biểu thức không phụ thuộc vào biến tức là sau khi rút gọn biểu thức ta được kết quả không chứa biến. Do đó, để giải dạng toán này, ta sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn. Nếu biểu thức sau khi thu gọn không chứa biến, ta suy ra điều phải chứng minh.
Xem thêm các bài viết liên quan hay, chi tiết:
Công thức lượng giác (2024) và cách giải bài tập chi tiết nhất
Câu 20:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Ta có :
suy ra
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Dựa theo định nghĩa các giá trị lượng giác trên đường tròn lượng giác.
Câu 22:
23/09/2024 Xem đáp án
Xem đáp án
Đáp án: C
*Lời giải
Vì là góc tù, nên ,
*Lý thuyết liên quan
- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho . Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là , được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là , được kí hiệu là cot α.
- Từ định nghĩa trên ta có:
- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:
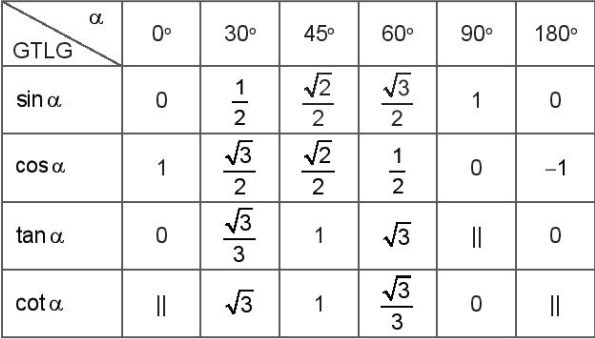 \
\
Xem thêm các bài toán hay, chi tiết khác
Lý thuyết Toán 10 Bài 5. Giá trị lượng giác của một góc từ 00 đến 1800– Kết nối tri thức
Giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Câu 23:
09/10/2024Cho bốn cung (trên một đường tròn định hướng): , , ,. Các cung nào có điểm cuối trùng nhau:
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Phương pháp giải:
- Nắm vững kiến thức về cung lượng giác: tách các cung lượng giác ban đầu để thấy được chu kì tuần hoàn ( điểm cuối ) của các cung
*Lời giải:
và ; và là các cặp góc lượng giác có điểm cuối trùng nhau.
*Các dạng bài góc, cung lượng giác:
* Độ dài cung tròn. Quan hệ giữa độ và rađian:
suy ra và
* Cách tính độ dài cung tròn
Phương pháp giải: Áp dụng công thức: , trong đó: l là độ dài cung tròn, R là bán kính đường tròn, là số đo bằng rad của cung.
Trường hợp có số đo bằng độ, ta có công thức:
a) Định nghĩa
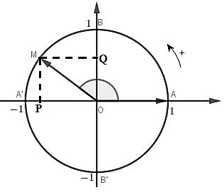
Trên đường tròn lượng giác cho cung có sđ , khi đó:
+) Tung độ của M gọi là sin của , kí hiệu là :
+) Hoành độ của M gọi là cosin của , kí hiệu là :
+) Nếu , tỉ số gọi là tang của , kí hiệu là :
+) Nếu , tỉ số gọi là côtang của , kí hiệu là :
Các giá trị ,,, được gọi là các giá trị lượng giác của cung . Ta cũng gọi trục tung là trục sin, trục hoành là trục cosin.
b. Hệ quả:
+) xác định với mọi giá trị của và .
+) được xác định khi , xác định khi
+)
+)
c) Các công thức lượng giác cơ bản:

Xem thêm các bài viết liên quan hay, chi tiết:
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 6 (có đáp án) (669 lượt thi)
- 100 câu trắc nghiệm Cung và góc lượng giác cơ bản (1588 lượt thi)
- 100 câu trắc nghiệm Cung và góc lượng giác nâng cao (2013 lượt thi)
- Trắc nghiệm Ôn tập chương 6 Cung và góc lượng giác công thức lượng giác có đáp án (562 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Nhận biết) (301 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Thông hiểu) (365 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Vận dụng) (432 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (358 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Công thức lượng giác (có đáp án) (2213 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một cung (có đáp án) (1278 lượt thi)
- Trắc nghiệm Cung và góc lượng giác (có đáp án) (887 lượt thi)
- Trắc nghiệm: Giá Trị lượng giác của một cung có đáp án (573 lượt thi)
- Trắc nghiệm Giá trị có lượng giác của một cung có đáp án (556 lượt thi)
- Trắc nghiệm Góc và cung lượng giác có đáp án (542 lượt thi)
- Trắc nghiệm Cung và góc lượng giác có đáp án (Nhận biết) (523 lượt thi)
- Trắc nghiệm Giá trị có lượng giác của một cung có đáp án (Nhận biết) (504 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Nhận biết) (488 lượt thi)
- Trắc nghiệm Cung và góc lượng giác có đáp án (Thông hiểu) (487 lượt thi)
