Cho bốn cung (trên một đường tròn định hướng): $\alpha =-\frac{5\pi }{6}$, $\beta =\frac{\pi }{\text{3}}$,$\gamma =\frac{\text{25}\pi }{\text{3}}$ ,$\delta =\frac{\text{19}\pi }{\text{6}}$. Các cung nào có điểm cuối trùng nhau:

Đáp án đúng: B

*Phương pháp giải:

- Nắm vững kiến thức về cung lượng giác: tách các cung lượng giác ban đầu để thấy được chu kì tuần hoàn ( điểm cuối ) của các cung 

*Lời giải:

$$\begin{gathered} \alpha =-\frac{5\pi }{6}=\frac{7\pi }{6}-2\pi ; \\ \gamma =\frac{\text{25}\pi }{\text{3}}=\frac{\pi }{\text{3}}+8\pi ; \\ \delta =\frac{\text{19}\pi }{\text{6}}=\frac{7\pi }{\text{6}}+2\pi \end{gathered}$$

$\Rightarrow \beta$ và $\gamma$; $\alpha$ và $\delta$ là các cặp góc lượng giác có điểm cuối trùng nhau.

*Các dạng bài góc, cung lượng giác:

* Độ dài cung tròn. Quan hệ giữa độ và rađian:

${180}^o=\pi rad$ suy ra $1^o=\frac{\pi }{180}rad$ và$1rad={\left(\frac{180}{\pi }\right)}^o$

* Cách tính độ dài cung tròn

Phương pháp giải: Áp dụng công thức: $l=R\alpha$, trong đó: l là độ dài cung tròn, R là bán kính đường tròn,$\alpha$ là số đo bằng rad của cung.

Trường hợp $\alpha$ có số đo bằng độ, ta có công thức: $l=R.\frac{\pi .\alpha }{180}$

a) Định nghĩa

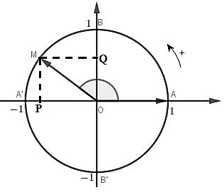
Trên đường tròn lượng giác cho cung $\stackrel{\curvearrowright }{AM}$ có sđ $\stackrel{\curvearrowright }{AM}=\alpha$, khi đó:

+) Tung độ của M gọi là sin của $\alpha$, kí hiệu là $\sin \alpha$: $\sin \alpha =\overline{OQ}$

+) Hoành độ của M gọi là cosin của $\alpha$, kí hiệu là $cos\alpha$: $cos\alpha =\overline{OP}$

+) Nếu $cos\alpha \ne 0$, tỉ số $\frac{\sin \alpha }{cos\alpha }$ gọi là tang của $\alpha$, kí hiệu là $\tan \alpha$: $\tan \alpha =\frac{\sin \alpha }{cos\alpha }$

+) Nếu $\sin \alpha \ne 0$, tỉ số $\frac{cos\alpha }{\sin \alpha }$ gọi là côtang của $\alpha$, kí hiệu là $\cot \alpha$: $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

Các giá trị $\sin \alpha$,$cos\alpha$,$\tan \alpha$,$\cot \alpha$ được gọi là các giá trị lượng giác của cung $\alpha$. Ta cũng gọi trục tung là trục sin, trục hoành là trục cosin.

b. Hệ quả:

+) $\sin \alpha ,\cos \alpha$ xác định với mọi giá trị của $\alpha$ và $-1\le \sin \alpha \le 1,-1\le \cos \alpha \le 1$.

+) $\tan \alpha$ được xác định khi $\alpha \ne \frac{\pi }{2}+k\pi$, xác định khi $\alpha \ne k\pi$

+) $\sin \alpha =\sin \left(\alpha +k2\pi \right),\cos \alpha =\cos \left(\alpha +k2\pi \right)$

+) $\tan \alpha =\tan \left(\alpha +k\pi \right),\cot \alpha =\cot \left(\alpha +k\pi \right)$

c) Các công thức lượng giác cơ bản:

Xem thêm các bài viết liên quan hay, chi tiết:

100 câu trắc nghiệm Cung và góc lượng giác nâng cao 

Trắc nghiệm Ôn tập chương 6 Cung và góc lượng giác công thức lượng giác có đáp án

Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Vận dụng)