Giải SBT Toán 10 trang 92 Tập 1 Cánh diều

Với Giải SBT Toán 10 trang 92 Tập 1 trong Bài 4: Tổng và hiệu của hai vectơ Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 92.

1 3387 lượt xem

Trang trước

Trang sau

Bài 32 trang 92 SBT Toán 10 Tập 1: Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?

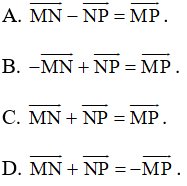
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Lời giải:

Đáp án đúng là C

Ta có: $\vec{M N} - \vec{N P} = \vec{M N} + \vec{P N}$ $= \vec{M N} + \vec{M K} = \vec{M H} \neq \vec{M P}$ (H, K là điểm thỏa mãn MKHN là hình bình hành). Do đó A sai.

Ta có: $- \vec{M N} + \vec{N P} = \vec{N M} + \vec{N P} = \vec{N T} \neq \vec{M P}$ (T là điểm MNPT là hình bình hành). Do đó B sai

Ta có: $\vec{M N} + \vec{N P} = \vec{M P}$ (quy tắc ba điểm). Do đó C đúng.

Ta có: $\vec{M N} + \vec{N P} = \vec{M P} \neq - \vec{M P}$ . Do đó D sai.

Bài 33 trang 92 SBT Toán 10 Tập 1: Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây đúng?

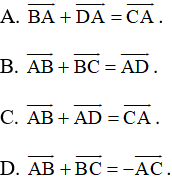
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Lời giải:

Đáp án đúng là A

Ta có: $\vec{B A} + \vec{D A} = \vec{B A} + \vec{C B}$ $= \vec{C B} + \vec{B A} = \vec{C A}$ . Do đó A đúng.

Ta có: $\vec{A B} + \vec{B C} = \vec{A C} \neq \vec{A D}$ . Do đó B sai.

Ta có: $\vec{A B} + \vec{A D} = \vec{A C} \neq \vec{C A}$ . Do đó C sai.

Ta có: $\vec{A B} + \vec{B C} = \vec{A C} \neq - \vec{A C}$ . Do đó D sai.

Bài 34 trang 92 SBT Toán 10 Tập 1: Cho các điểm A, B, O. Khẳng định nào sau đây đúng?

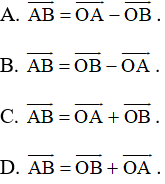
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Lời giải:

Đáp án đúng là B

Cho các điểm A, B, O. Khẳng định nào sau đây đúng?

Ta có: $\vec{O A} - \vec{O B} = \vec{O A} + \vec{B O}$ $= \vec{B O} + \vec{O A} = \vec{B A} \neq \vec{A B}$ . Do đó A sai.

Ta có: $\vec{O B} - \vec{O A} = \vec{O B} + \vec{A O}$ $= \vec{A O} + \vec{O B} = \vec{A B}$ . Do đó B đúng.

Ta có: $\vec{O A} + \vec{O B} = \vec{O C} \neq \vec{A B}$ (C là điểm thỏa mãn OBCA là hình bình hành). Do đó C sai.

Ta có: $\vec{O B} + \vec{O A} = \vec{O C} \neq \vec{A B}$ (C là điểm thỏa mãn OBCA là hình bình hành). Do đó D sai.

Bài 35 trang 92 SBT Toán 10 Tập 1: Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để M là trung điểm của đoạn thẳng AB là:

A. $\vec{M A} = \vec{M B}$ .

B. $|\vec{M A}| = |\vec{M B}|$ .

C. $\vec{M A}, \vec{M B}$ ngược hướng.

D. $\vec{M A} + \vec{M B} = \vec{0}$ .

Lời giải:

Đáp án đúng là D

M là trung điểm của đoạn thẳng AB thì MA = MB và $\vec{M A}, \vec{M B}$ ngược hướng.

⇒ $\vec{M A} = - \vec{M B}$ hay $\vec{M A} + \vec{M B} = \vec{0} .$

Vậy điều kiện đủ đề M là trung điểm của đoạn thẳng AB là $\vec{M A} + \vec{M B} = \vec{0} .$

Bài 36 trang 92 SBT Toán 10 Tập 1: Cho tam giác ABC. Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là:

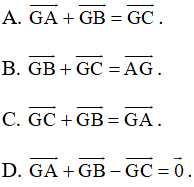
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Lời giải:

Đáp án đúng là B

Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

⇔ $\vec{G B} + \vec{G C} = - \vec{G A}$

⇔ $\vec{G B} + \vec{G C} = \vec{A G}$

Bài 37 trang 92 SBT Toán 10 Tập 1: Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh: $\vec{O C} + \vec{O D} = \vec{A C} + \vec{B D} .$

Lời giải:

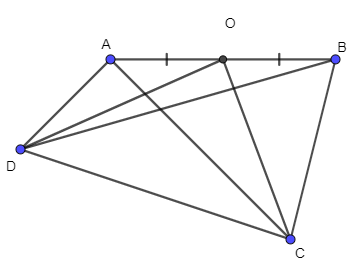
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Ta có:

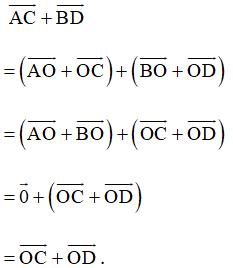
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Bài 38 trang 92 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A, AB = 4a, AC = 5a. Tính:

a) $|\vec{A B} - \vec{A C}|$ ;

b) $|\vec{A B} + \vec{A C}|$ .

Lời giải:

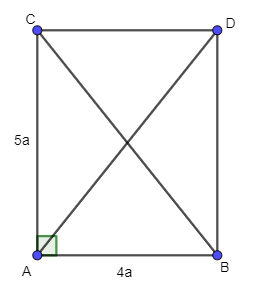
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

a) Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí pythagoras)

⇔ BC² = (4a)² + (5a)² = 41a²

⇔ BC = $\sqrt{41}$ a.

Ta có:

$\vec{A B} - \vec{A C} = \vec{A B} + \vec{C A} = \vec{C A} + \vec{A B} = \vec{C B}$

⇒ $|\vec{A B} - \vec{A C}| = |\vec{C B}| = \sqrt{41} a$ .

Vậy $|\vec{A B} - \vec{A C}| = \sqrt{41} a$ .

b) Lấy điểm D là điểm thỏa mãn ABDC là hình chữ nhật nên AD = BC (tính chất hình hình chữ nhật).

Ta có: $\vec{A B} + \vec{A C} = \vec{A D}$ (quy tắc hình bình hành)

⇒ $|\vec{A B} + \vec{A C}| = |\vec{A D}| = |\vec{C B}| = \sqrt{41} a$ .

Vậy $|\vec{A B} + \vec{A C}| = \sqrt{41} a .$

Bài 39 trang 92 SBT Toán 10 Tập 1: Cho tam giác đều ABC cạnh a. Tính:

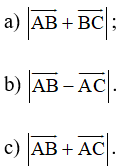
Sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

Lời giải:

a) Ta có: $\vec{A B} + \vec{B C} = \vec{A C}$ (quy tắc 3 điểm)

⇒ $|\vec{A B} + \vec{B C}| = |\vec{A C}| = A C = a$

Vậy $|\vec{A B} + \vec{B C}| = a$ .

b) Ta có:

$\vec{A B} - \vec{A C} = \vec{A B} + \vec{C A} = \vec{C A} + \vec{A B} = \vec{C B}$

⇒ $|\vec{A B} - \vec{A C}| = |\vec{C B}| = C B = a$ .

Vậy $|\vec{A B} - \vec{A C}| = a$ .

c) Gọi D là điểm thỏa mãn ABDC là hình bình hành, M là trung điểm của BC.

Khi đó: $\vec{A B} + \vec{A C} = \vec{A D}$

⇒ $|\vec{A B} + \vec{A C}| = |\vec{A D}|$ .

Xét tam giác ABC, có AM là đường trung tuyến nên AM là đường cao

⇒ AM = $\frac{a \sqrt{3}}{2}$

⇒ AD = 2AM = 2. $\frac{a \sqrt{3}}{2} = a \sqrt{3}$ .

⇒ $|\vec{A B} + \vec{A C}| = |\vec{A D}| = a \sqrt{3}$ .

Vậy $|\vec{A B} + \vec{A C}| = a \sqrt{3}$ .

Bài 40 trang 92 SBT Toán 10 Tập 1: Cho tam giác ABC thỏa mãn $|\vec{A B} + \vec{A C}| = |\vec{A B} - \vec{A C}|$ . Chứng minh tam giác ABC vuông tại A.