Nội dung bài viết

    Xem thêm

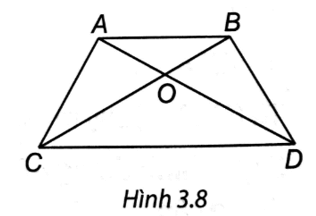
    Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD

    Lời giải Câu 3 trang 47 VTH Toán 8 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Vở thực hành Toán 8.

    1 697 11/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Vở thực hành Toán 8 Bài 11: Hình thang cân

    Câu 3 trang 47 VTH Toán 8 Tập 1: Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).

    Cho hình thang ABCD có AB song song CD, hai đường chéo AC và BD

    Trong các khẳng định sau, khẳng định sai là

    A. BC = AD.

    B. ABCD là hình thang cân.

    C. AC = BD.

    D. Tam giác AOC cân tại O.

    Lời giải:

    Đáp án đúng là: D

    Ta có: OA = OB; OC = OD suy ra OA + OC = OB + OD

    Khi đó AC = BD nên ABCD là hình thang cân. Do đó B, C đúng.

    ABCD là hình thang cân nên hai cạnh bên bằng nhau nên BD = AC. Do đó A đúng.

    Vì A, O, C thẳng hàng nên D là khẳng định sai.

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Câu 1 trang 47 VTH Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống. a) Hình thang cân là ..................................... bằng nhau...

    Câu 2 trang 47 VTH Toán 8 Tập 1: Cho hình thang ABCD cân (AB // CD) có C^=60° (H.3.7). Khi đó, số đo D^1 bằng...

    Câu 3 trang 47 VTH Toán 8 Tập 1: Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8)...

    Bài 1 trang 48 VTH Toán 8 Tập 1: Hình thang trong Hình 3.9 có là hình thang cân không? Vì sao...

    Bài 2 trang 48 VTH Toán 8 Tập 1: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED...

    Bài 3 trang 48 VTH Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E...

    Bài 4 trang 49 VTH Toán 8 Tập 1: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J...

    Bài 5 trang 49 VTH hành Toán 8 Tập 1: Cho hình thang cân ABCD có đáy nhỏ BC. Hạ BH ⊥ AD, CE ⊥ AD. a) Chứng minh AH = ED...

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 10: Tứ giác

    Luyện tập chung trang 49

    Bài 12: Hình bình hành

    Luyện tập chung trang 54

    Bài 13: Hình chữ nhật

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 697 11/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: