Nội dung bài viết

    Xem thêm

    Giải Vở thực hành Toán 8 (Kết nối tri thức) Luyện tập chung trang 13

    Với giải Vở thực hành Toán 8 Luyện tập chung trang 13 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 8.

    1 1,264 09/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải VTH Toán 8 Luyện tập chung trang 13  

    Bài 1 trang 13 VTH Toán 8 Tập 1: Cho các biểu thức:

    45x; 2−1xy; −3xy2; 12x2y; 1xy3; −xy+2; −32x2y; x5.

    a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?

    b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.

    c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.

    Lời giải:

    a) Biểu thức 1xy3 không là đơn thức.

    Biểu thức −xy+2 không là đơn thức.

    Biểu thức x5 không là đơn thức.

    Các biểu thức còn lại đều là đơn thức.

    b) - Đơn thức 45x có hệ số là 45 và phần biến là x.

    - Đơn thức 2−1xy có hệ số là 2−1 và phần biến là xy.

    - Đơn thức −3xy2 có hệ số là −3 và phần biến là xy2.

    - Đơn thức 12x2y có hệ số là 12 và phần biến là x2y.

    - Đơn thức −32x2y có hệ số là −32 và phần biến là x2y.

    c) Tổng tất cả các đơn thức trên là:

    45x+2−1xy+−3xy2+12x2y+−32x2y

    = 45x+2−1xy−3xy2−x2y.

    Đa thức 45x+2−1xy−3xy2−x2y có bậc là 3.

    Bài 2 trang 14 VTH Toán 8 Tập 1: Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy là hình chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.

    a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.

    b) Tính lượng nước bơm đầy bể nếu x = 5 m, y = 3 m.

    Lời giải:

    a) Bể thứ nhất có chiều sâu 1,2 m với hai kích thước đáy là x và y nên có dung tích V1 = 1,2xy (m3). Bể thứ hai có chiều sâu 1,5 m với các kích thước đáy là 5x và 5y nên có dung tích là V2 = 1,5.5x.5y = 37,5xy (m3).

    Do đó số mét khối nước cần có để bơm đầy cả hai bể bơi là

    V = V1 + V2 = 1,2xy + 37,5xy = (1,2 + 37,5)xy = 38,7xy (m3).

    b) Khi x = 5 m, y = 3 m, lượng nước bơm đầy hai bể là

    V = 38,7.5.3 = 580,5 (m3).

    Bài 3 trang 14 VTH Toán 8 Tập 1: Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = −2.

    a) P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3.

    b) Q = x3 + x2y – xy2 – x2y – xy2 – x3.

    Lời giải:

    a) P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3

    = 5x4 – (3x3y + x3y) + (2xy3 – 2xy3) + 2y4 – 7x2y2

    = 5x4 – 4x3y + 2y4 – 7x2y2.

    Tất cả các hạng tử đều có bậc 4.

    Vậy P là đa thức bậc 4.

    Tại x = 1; y = −2, ta có

    P=5.14−4.13.−2+2.−24−7.12.−22=17.

    b) Q = x3 + x2y – xy2 – x2y – xy2 – x3

    = (x3 – x3) + (x2y – x2y) – (xy2 + xy2) = –2xy2.

    Đa thức Q có bậc là 3.

    Tại x = 1; y = −2, ta có:

    Q = –2xy2 = –2.1.(−2)2 = –2.4 = –8.

    Bài 4 trang 14 VTH Toán 8 Tập 1: Cho hai đa thức:

    A = 7xyz2 – 5xy2z + 3x2yz – xyz + 1; B = 7x2yz – 5xy2z + 3xyz2 – 2.

    a) Tìm đa thức C sao cho A – C = B.

    b) Tìm đa thức D sao cho A + D = B.

    c) Tìm đa thức E sao cho E – A = B.

    Lời giải:

    a) C = A – B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) – (7x2yz – 5xy2z + 3xyz2 – 2)

    = 7xyz2 – 5xy2z + 3x2yz – xyz + 1 – 7x2yz + 5xy2z – 3xyz2 + 2

    = (7xyz2 – 3xyz2) + (5xy2z – 5xy2z) + (3x2yz – 7x2yz) – xyz + (1 + 2)

    = 4xyz2 – 4x2yz – xyz + 3.

    b) D = B – A = –(A – B) = –(4xyz2 – 4x2yz – xyz + 3)

    = –4xyz2 + 4x2yz + xyz – 3.

    c) E = A + B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) + (7x2yz – 5xy2z + 3xyz2 – 2)

    = 7xyz2 – 5xy2z + 3x2yz – xyz + 1 + 7x2yz – 5xy2z + 3xyz2 – 2

    = (7xyz2 + 3xyz2) – (5xy2z + 5xy2z) + (7x2yz + 3x2yz) – xyz + (1 – 2)

    = 10x2yz – 10xy2z + 10xyz2 – xyz + 3.

    Bài 5 trang 15 VTH Toán 8 Tập 1: Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimét) như hình bên. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?

    Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét

    Lời giải:

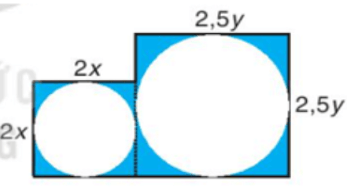
    Miếng bìa gồm có hai hình vuông có cạnh lần lượt là 2x và 2,5y ghép lại. Do đó diện tích của miếng bìa là 2x.2x + 2,5y.2,5y = 4x2 + 6,25y2.

    Tổng diện tích hai hình tròn cắt ra là (2x)2.π + (2,5y)2.π = 4πx2 + 6,25πy2.

    Vậy diện tích phần còn lại của miếng bìa là

    (4x2 + 6,25y2) − (4πx2 + 6,25πy2) = 4(1 − π)x2 + 6,25(1 − π)y2.

    Đó là một đa thức bậc 2.

    Bài 6 trang 15 VTH Toán 8 Tập 1: Cho ba đa thức: M = 3x3 – 4x2y + 3x – y; N = 5xy – 3x + 2; P = 3x3 + 2x2y + 7x – 1.

    Tính M + N – P và M – N – P.

    Lời giải:

    +) N + N − P = (3x3 – 4x2y + 3x – y) + (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)

    = 3x3 – 4x2y + 3x – y + 5xy – 3x + 2 – 3x3 – 2x2y – 7x + 1

    = (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)

    = – 6x2y + 5xy – 7x – y + 3.

    +) M – N – P = (3x3 – 4x2y + 3x – y) – (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)

    = 3x3 – 4x2y + 3x – y + 5xy + 3x – 2 – 3x3 – 2x2y – 7x + 1

    = (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x + 3x – 7x) – y + (1 – 2)

    = – 6x2y + 5xy – x – y – 1.

    Bài 7 trang 16 VTH Toán 8 Tập 1: Cho hai đa thức A = x2y2 − axy2 + 3y2 − xy + b, và B = cx2y2 + 2xy2 − dy2 + 4, trong đó a, b, c, d là các số thực. Biết rằng A + B = −2x2y2 + 3y2 − xy − 1. Hãy tìm các số a, b, c và d.

    Lời giải:

    Ta có:

    A + B = (x2y2 − axy2 + 3y2 − xy + b) + (cx2y2 + 2xy2 − dy2 + 4)

    = (1 + c)x2y2 + (2 − a)xy2 + (3 − d)y2 − xy + (b + 4).

    Theo đề bài, (1 + c)x2y2 + (2 − a)xy2 + (3 − d)y2 − xy + (b + 4) = −2x2y2 + 3y2 − xy − 1.

    So sánh hệ số của các hạng tử đồng dạng ở hai vế, ta có:

    1 + c = −2 (hệ số của x2y2), suy ra c = −3; 3 − d = 3 (hệ số của y2), suy ra d = 0; 2 − a = 0 (hệ số của xy2), suy ra a = 2; b + 4 = −1 (hệ số tự do), suy ra b = −5.

    Vậy đáp số của bài toán là a = 2, b = −5, c = −3 và d = 0.

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 3: Phép cộng và phép trừ đa thức

    Bài 4: Phép nhân đa thức

    Bài 5: Phép chia đa thức cho đơn thức

    Luyện tập chung trang 21

    Bài tập cuối chương 1

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,264 09/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: