Nội dung bài viết

    Xem thêm

    Giải Vở thực hành Toán 8 (Kết nối tri thức): Bài tập cuối chương 4

    Với giải Vở thực hành Toán 8 Bài tập cuối chương 4 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 8.

    1 615 12/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải VTH Toán 8 Bài tập cuối chương 4 - Kết nối tri thức

    A – CÂU HỎI TRẮC NGHIỆM

    Chọn phương án đúng trong mỗi câu sau:

    Câu 1 trang 79 vở thực hành Toán 8 Tập 1: Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

    A. 3,5 cm.

    B. 7 cm.

    C. 10 cm.

    D. 15 cm.

    Lời giải:

    Đáp án đúng là: B

    Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra HK=12AB.

    Do đó AB = 2HK = 2 . 3,5 = 7 (cm).

    Vậy AB = 7 cm.

    Câu 2 trang 79 vở thực hành Toán 8 Tập 1: Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

    A. 8 cm.

    B. 64 cm.

    C. 30 cm.

    D. 16 cm.

    Lời giải:

    Đáp án đúng là: D

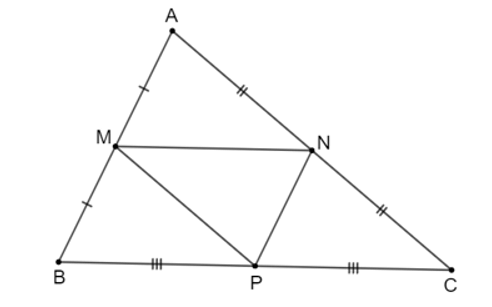
    Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt

    • Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN=12BC.

    • Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP=12AB.

    • Vì M, P lần lượt là trung điểm của các cạnh AB, BC nên MP là đường trung bình của tam giác ABC suy ra MP=12AC.

    Chu vi tam giác ABC bằng: AB + BC + CA = 32 (cm).

    Chu vi tam giác MNP bằng:

    MN+NP+MP=12BC+12AB+12AC

    =12AB+BC+CA=12.32=16  cm.

    Vậy chu vi tam giác MNP bằng 16 cm.

    Câu 3 trang 80 vở thực hành Toán 8 Tập 1: Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng

    A. 4 cm.

    B. 5 cm.

    C. 6 cm.

    D. 7 cm.

    Lời giải:

    Đáp án đúng là: A

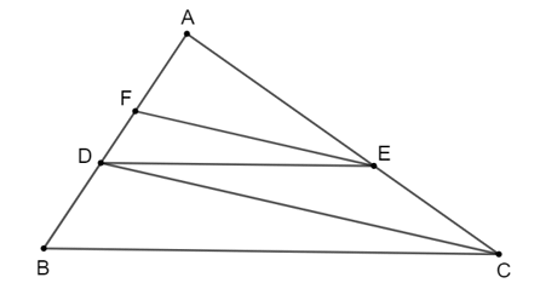
    Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB

    Áp dụng định lí Thalès:

    • Với DE // BC (E ∈ AC) ta có: AEAC=ADAB=912=23.

    • Với EF // CD (F ∈ AB) ta có: AFAD=AEAC=23.

    Suy ra AF=23AD=23.6=4  cm.

    Vậy AF = 4 cm.

    B – BÀI TẬP

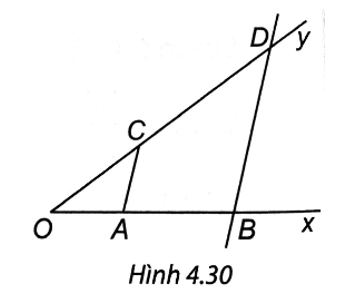
    Bài 4 trang 80 vở thực hành Toán 8 Tập 1: Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.

    Lời giải:

    Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm

    AB = OB – OA = 5 – 2 = 3 cm.

    Ta có AC // BD nên theo định lí Thales ta có: OAAB=OCCD nên 23=3CD suy ra CD = 4,5 cm.

    Bài 5 trang 80 vở thực hành Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

    a) Chứng minh rằng AE = DF.

    b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

    Lời giải:

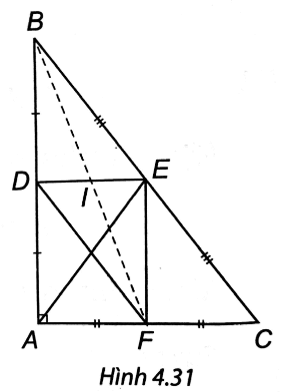
    Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB

    a) ∆ABC có: D là trung điểm AB, E là trung điểm BC, nên DE là đường trung bình của ∆ABC.

    Suy ra DE // AC và DE = 12AC.

    Xét tứ giác ADEF: DE // AF và DE = AF nên tứ giác ADEF là hình bình hành.

    Ta lại có DAF^=90° nên tứ giác ADEF là hình chữ nhật.

    Suy ra AE = DF.

    b) ∆ABC có: D là trung điểm AB, F là trung điểm AC nên DF là đường trung bình của ∆ABC.

    Suy ra DF // BC và DF = 12BC = BE.

    Xét tứ giác BDFE: DF // BE và DF = BE nên tứ giác BDFE là hình bình hành.

    Suy ra hai đường chéo DE và BF cắt nhau tại trung điểm của mỗi đường.

    Ta lại có I là trung điểm của DE nên I cũng là trung điểm của BF.

    Vậy B, I, F thẳng hàng.

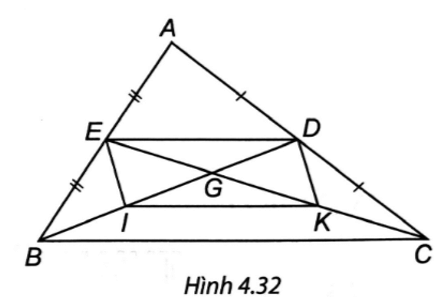
    Bài 6 trang 81 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

    Lời giải:

    Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G

    ∆ABC có: E là trung điểm AB, D là trung điểm AC nên ED là đường trung bình của ∆ABC. Suy ra ED // BC và ED = 12BC. (1)

    ∆GBC có: I là trung điểm GC, K là trung điểm GB nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và IK = 12BC. (2)

    Từ (1) và (2) suy ra ED // IK và ED = IK nên tứ giác EDKI là hình bình hành.

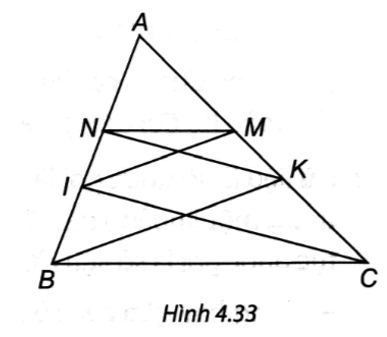
    Bài 7 trang 81 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB). Chứng minh MN song song với BC.

    Lời giải:

    Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC

    NK // IC suy ra ANAI=AKAC (định lí Thalès trong tam giác) nên AN . AC = AI . AK. (1)

    IM // BK suy ra AIAB=AMAK (định lí Thalès trong tam giác) nên AM . AB = AI . AK. (2)

    Từ (1) và (2) suy ra: AN . AC = AM . AB (= AI . AK).

    Suy ra ANAB=AMAC nên MN // BC (định lí Thalès đảo).

    Bài 8 trang 81 vở thực hành Toán 8 Tập 1: Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.34. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

    Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá

    Lời giải:

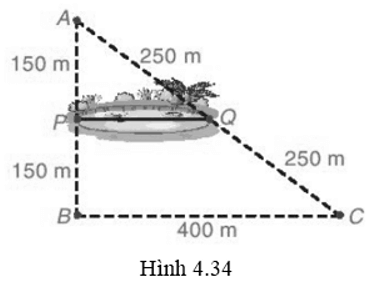
    ∆ABC có: P là trung điểm AB, Q là trung điểm AC nên PQ là đường trung bình của ∆ABC. Suy ra PQ // BC và PQ = 12BC = 200 m.

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Luyện tập chung trang 77

    Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

    Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

    Luyện tập chung trang 96

    Bài tập cuối chương 5

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 615 12/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: