Nội dung bài viết

    Xem thêm

    Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc

    Lời giải Bài 43 trang 61 SBT Toán 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 888 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 Cánh diều Bài 5: Hai dạng phương trình quy về phương trình bậc hai

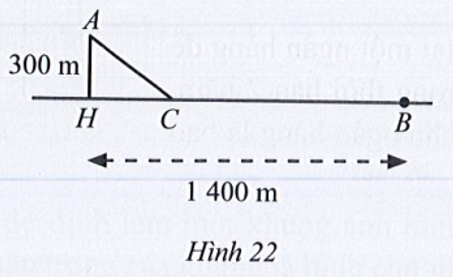
    Bài 43 trang 61 SBT Toán 10 Tập 1: Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300m và gặp người đi bộ tại địa điểm cách B một khoảng BH = 1 400m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).

    a) Tính khoảng cách CB.

    b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc.

    Sách bài tập Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai - Cánh diều (ảnh 1)

    Lời giải

    a) Đặt CH = x (x ≥ 0). Khi đó BC = 1 400 – x.

    Xét tam giác AHC vuông tại H, có:

    AH2 + HC2 = AC2

    ⇔ AC2 = 3002 + x2

    ⇔ AC = x2+90 000

    Thời gian thuyền đi từ A đến C là: x2+90 0003 (giờ)

    Thời gian người đi bộ đi từ B đến C là 1 400−x6 (giờ)

    Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C nên ta có:

    x2+90 0003= 1 400−x6

    ⇔ 2x2+90 000= 1400−x (điều kiện x ≤ 1 400)

    ⇔ 4(x2 + 90 000) = 1 960 000 – 2 800x + x2

    ⇔ 3x2 + 2 800x – 1 600 000 = 0

    ⇔ x = 400 (TMĐK) hoặc x = −40003 (không TMĐK)

    ⇒ CB = 1 400 – x = 1 400 – 400 = 1 000 (m).

    Vậy khoảng cách CB = 1 000 m.

    b) Đổi 1 000 m = 1km.

    Thời gian hai nguời xuất phát cho tới khi gặp nhau là: 16(giờ)

    Vậy từ khi xuất phát hai người mất 16 giờ cho đến khi gặp nhau.

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 36 trang 59 SBT Toán 10 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?...

    Bài 37 trang 60 SBT Toán 10 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?...

    Bài 38 trang 60 SBT Toán 10 Tập 1: Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình...

    Bài 39 trang 60 SBT Toán 10 Tập 1: Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình...

    Bài 40 trang 60 SBT Toán 10 Tập 1: Giải các phương trình sau:...

    Bài 41 trang 60 SBT Toán 10 Tập 1: Giải các phương trình sau:...

    Bài 42 trang 60 SBT Toán 10 Tập 1: Để leo lên một bức tường, bác Dũng dùng một chiếc thang...

    Bài 43 trang 61 SBT Toán 10 Tập 1: Một người đi bộ xuất phát từ B trên một bờ sông (coi là...

    Bài 44 trang 61 SBT Toán 10 Tập 1: Người ta muốn thiết kế một vườn hoa hình chữ nhật nội...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài ôn tập chương 2

    Bài 1: Hàm số và đồ thị

    Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

    Bài 3: Dấu của tam thức bậc hai

    Bài 4: Bất phương trình bậc nhất một ẩn

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 888 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: