Lý thuyết Tổng hợp kiến thức cơ bản lớp 3

Lý thuyết Tổng hợp kiến thức cơ bản lớp 3

1) Cách đọc, viết các số có 4, 5 chữ số

a) Ví dụ: Lưu ý cho học sinh cách đọc số có chữ số 0; 1 ; 4; 5

- Khi nào đọc là “không’’, “mươi” (2032; 2320)

2032: Hai nghìn không trăm ba mươi hai

2320: Hai nghìn ba trăm hai mươi

- Khi nào đọc là “một”, “mốt” (1326; 3261)

1326: Một nghìn ba trăm hai mươi sáu

3261: Ba nghìn hai trăm sáu mươi mốt

- Khi nào đọc là “bốn”, “tư” (4526; 5264)

4526: Bốn nghìn năm trăm hai mươi sáu

5264: Năm nghìn hai trăm sáu mươi tư

- Khi nào đọc là “năm”, “lăm” (5378, 7835)

5378: Năm nghìn ba trăm bảy mươi tám

7835: Bảy nghìn tám trăm ba mươi lăm

b) Lưu ý viết số

Ví dụ. Năm mươi hai nghìn bốn trăm ba mươi sáu. Viết là: 52436.

Ví dụ. Viết số gồm: 5 chục nghìn, 2 nghìn, 4 trăm, 3 chục và 6 đơn vị. Viết là: 52436.

2. So sánh các số trong phạm vi 10000; 100000

Các bước so sánh:

+) Bước 1: So sánh số các chữ số.

+) Bước 2: So sánh từng hàng của 2 số kể từ hàng lớn nhất.

Ví dụ. So sánh: 45367 ... 45673.

Ta thấy 2 số đều có 5 chữ số.

So sánh từng hàng: Hàng chục nghìn bằng nhau, hàng nghìn bằng nhau, hàng trăm 3 < 6.

Vậy: 45367 < 45673.

3. Phép cộng, phép trừ các số trong phạm vi 10000, 100000

- Lưu ý học sinh đặt tính theo cột dọc, đặt thẳng các hàng từ phải sang trái. Nhớ chính xác khi thực hiện phép tính.

Ví dụ. Đặt tính rồi tính:

a) 18257 + 64439

b) 35046 – 26734

Bài giải

a) $\frac{+\begin{array}{c}18257\\ 64439\end{array}}{82696}$

b) $\frac{-\begin{array}{c}35046\\ 26734\end{array}}{8312}$

4. Phép nhân, phép chia các số có 4; 5 chữ số với (cho) số có 1 chữ số

- Lưu ý học sinh đặt tính đúng, thực hiện phép nhân từ phải sang trái, Thực hiện phép chia từ trái sang phải.

Ví dụ. Đặt tính rồi tính:

a) 14273 × 3

b) 37648 : 4

Bài giải

a)

$\frac{\times \begin{array}{c}14273\\ 3\end{array}}{42819}$

b)

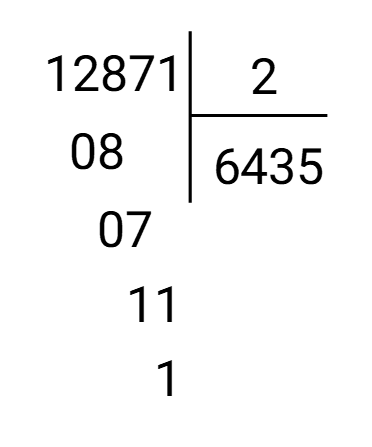
5. Thiết lập số có 4; 5 chữ số

Ví dụ. Viết tất cả các số có 4 chữ số khác nhau từ các chữ số: 1; 2; 3; 4 trong đó có chữ số hàng đơn vị là 4.

Ta lập được các số: 1234; 1324; 2134; 2314; 3214; 3124.

6. Nêu quy luật của dãy số, viết số thích hợp vào chỗ chấm

VD: 13005; 13006; 13007;...;...; ...;

Quy luật của dãy số trên là số đứng liền sau hơn số đứng liền trước 1 đơn vị.

7. Tìm thành phần chưa biết trong phép tính.

*) Phép cộng

Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng biết.

Ví dụ. Tìm x, biết:

x + 35974 = 83046

x = 83046 – 35974

x = 47072

*) Phép trừ

Muốn tìm số bị trừ ta thấy hiệu cộng với số trừ.

Muốn tìm số trừ, ta thấy số bị trừ trừ đi hiệu.

Ví dụ. Tìm x, biết:

a)

x – 234 = 432

x = 234 + 432

x = 666

b)

722 – x = 320

x = 722 – 320

x = 402

*) Phép nhân

Muốn tìm thừa số chưa biết, ta lấy tích chia cho thừa số đã biết

Ví dụ. Tìm x, biết:

x × 9 = 810

x = 810 : 9

x = 90

*) Phép chia

Muốn tìm số bị chia ta lấy thương nhân số chia.

Muốn tìm số chia ta lấy số bị chia chia cho thương.

Ví dụ. Tìm x, biết:

a)

x : 2 = 436

x = 436 × 2

x = 872

b)

965 : x = 5

x = 965 : 5

x = 193

GAM

Gam là một đơn vị đo khối lượng.

Gam viết tắt là g.

1000g = 1kg

Ngoài các quả cân 1kg, 2kg, 5kg còn có các quả cân: 1g, 2g, 5g; 10g, 20g, 50g,…

TÍNH GIÁ TRỊ CỦA BIỂU THỨC

*) Dạng 1: Biểu thức không có dấu ngoặc

+ Nếu trong biểu thức chỉ có các phép tính cộng, trừ thì ta thực hiện các phép tính theo thứ tự từ trái sang phải.

Ví dụ. 60 + 20 – 5 = 80 – 5 = 75

+ Nếu trong biểu thức chỉ có các phép tính nhân, chia thì ta thực hiện các phép tính theo thứ tự từ trái sang phải.

Ví dụ. 49 : 7 × 5 = 7 × 5 = 35

+ Nếu trong biểu thức có các phép tính cộng, trừ, nhân, chia thì ta thực hiện các phép tính nhân, chia trước, rồi thực hiện các phép tính cộng, trừ sau.

Ví dụ. 86 + 35 : 5 = 86 + 7 = 93

*) Dạng 2: Biểu thức có chứa dấu ngoặc

Khi tính giá trị của biểu thức có dấu ngoặc ( ) thì trước tiên ta thực hiện các phép tính trong ngoặc.

Ví dụ. 81 : (3 × 3) = 81 : 9 = 9

GIẢI TOÁN CÓ LỜI VĂN

1. Dạng toán về hơn kém số đơn vị

Ví dụ. Cuộn dây đỏ dài 1456m. Cuộn dây xanh dài hơn cuộn dây xanh 598m. Hỏi cả 2 cuộn dây dài bao nhiêu mét?

Tóm tắt:

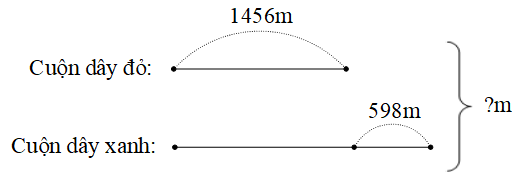
Bài giải

Cuộn dây xanh dài là:

1456 + 598 = 2054 (m)

Cả hai cuộn dây dài là:

1456 + 2054 = 3510 (m)

Đáp số: 3510m

2. Dạng toán về gấp, kém số lần

Ví dụ. Mảnh vải trắng dài 1569m, mảnh vải đen dài gấp 3 lần mảnh vải trắng. Hỏi cả 2 mảnh vải dài bao nhiêu mét?

Tóm tắt:

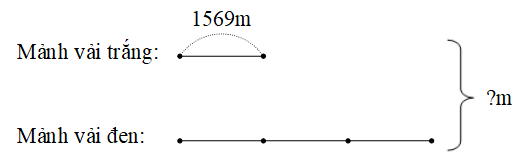
Bài giải

Mảnh vải đen dài là:

1569 × 3 = 4707 (m)

Cả hai mảnh vải dài là:

1569 + 4707 = 6276 (m)

Đáp số: 6276m

3. Dạng 3: Tìm 1 trong các phần bằng nhau của 1 số

Ví dụ. Cuộn dây xanh dài 9366m. Cuộn dây vàng dài bằng 1/3 cuộn dây xanh. Hỏi cả 2 cuộn dây dài bao nhiêu mét?

Tóm tắt:

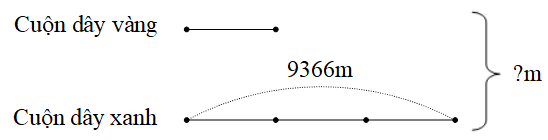
Bài giải

Cuộn dây vàng dài số mét là:

9366 : 3 = 3122 (m)

Cả hai cuộn dây dài là:

9366 + 3122 = 12488 (m)

Đáp số: 12488m

4. Dạng toán liên quan đến rút về đơn vị

Ví dụ 1. 3 hàng có 396 cây. Hỏi 5 hàng có bao nhiêu cây?

Tóm tắt:

3 hàng: 396 cây

5 hàng: ? cây

Bài giải

1 hàng có số cây là:

396 : 3 = 132 (cây)

5 hàng có số cây là:

132 × 5 = 660 (cây)

Đáp số: 660 cây

Ví dụ 2. 24 cái bát xếp vào 4 hộp. Hỏi có 42 cái bát xếp vào được bao nhiêu hộp như thế?

Tóm tắt:

24 cái bát: 4 hộp

42 cái bát: ? hộp

Bài giải

1 hộp bát có số cái bát là:

24 : 4 = 6 (cái bát)

42 cái bát được xếp vào số hộp là:

42 : 6 = 7 (hộp)

Đáp số: 7 hộp

SO SÁNH SỐ LỚN GẤP MẤY LẦN SỐ BÉ.

SỐ SÁNH SỐ BÉ BẰNG MỘT PHẦN MẤY SỐ LỚN.

Bài toán: Đoạn thẳng AB dài 6cm, đoạn thẳng CD dài 2cm. Hỏi đoạn thẳng AB dài gấp mấy lần đoạn thẳng CD?

Bài giải

Độ dài đoạn thẳng AB gấp độ dài đoạn thẳng CD số lần là:

6 : 2 = 3 (lần)

Độ dài đoạn thẳng CD gấp 3 lần độ dài đoạn thẳng AB.

Độ dài đoạn thẳng AB bằng $\frac{1}{3}$ độ dài đoạn thẳng CD.

LÀM QUEN VỚI CHỮ SỐ LA MÃ

Các chữ số La Mã từ I đến XXI

I	II	III	IV	V	VI
Một	Hai	Ba	Bốn	Năm	Sáu
VII	VIII	IX	X	XI	XII
Bảy	Tám	Chín	Mười	Mười một	Mười hai
XIII	XIV	XV	XVI	XVII	XVIII
Mười b	Mười bốn	Mười lăm	Mười sáu	Mười bảy	Mười tám

THỜI GIAN

*) Cách đọc giờ đúng: Giờ đúng là khi kim phút chỉ đúng vào số 12 và kim giờ chỉ bất kì vào số nào thì chính là giờ đúng của số đó.

Ví dụ.

Quan sát đồng hồ trên ta thấy: Kim phút chỉ vào số 12, kim giờ chỉ vào số 2.

Do đó, đồng hồ trên chỉ giờ đúng là 3 giờ.

*) Cách đọc giờ lẻ

Một giờ có 60 phút, 1 phút có 60 giây.

Trên mặt đồng hồ mỗi số cách nhau 5 đơn vị bắt đầu từ số 12.

Ví dụ.

Quan sát đồng hồ trên ta thấy: Kim phút chỉ vào số 6 nên ta lấy 5 × 6 = 30

Vậy đồng hồ trên chỉ 7 giờ 30 phút.

BẢNG ĐƠN VỊ ĐO ĐỘ DÀI

Lớn hơn mét			Mét	Bé hơn mét
km	hm	dam	m	dm	cm	mm
1km = 10hm = 1000m	1hm = 10dam = 100m	1dam = 10m	1m = 10dm = 100cm = 1000mm	1dm = 10cm = 100mm	1cm = 10mm	1mm

Nhận xét:

+ Mỗi đơn vị gấp 10 lần đơn vị liền sau.

Ví dụ: 1m = 10dm; 1km = 1000m

+ Mỗi đơn vị bằng $\frac{1}{10}$ đơn vị liền trước.

Ví dụ:

$1m=\frac{1}{10}dam$

HÌNH HỌC

1. Điểm ở giữa – trung điểm của đoạn thẳng

*) Điểm ở giữa

Quan sát hình vẽ ta thấy ba điểm O, A, B thẳng hàng; Điểm O nằm giữa hai điểm A và B.

*) Trung điểm của đoạn thẳng

Quan sát hình vẽ ta thấy, ba điểm A, O, B thẳng hàng (điểm O nằm giữa hai điểm A và B) và

AM = MB.

2. Hình tròn, tâm, bán kính, đường kính. 

*) Hình tròn tâm O

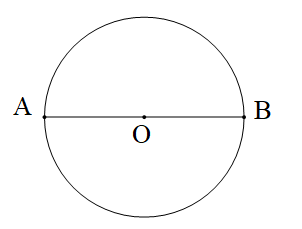
 - Đường kính AB đi qua tâm O

 - Bán kính OA = OB.

 - Bán kính bằng nửa đường kính:  OA = OB = AB : 2

3. Diện tích của 1 hình. Đơn vị đo diện tích. Xăng-ti-mét vuông.

- Bề mặt bên trong của 1 hình nào đó chính là diện tích của hình đó.

- Để đo diện tích ta dùng đơn vị đo diện tích, chẳng hạn: xăng-ti-mét vuông

- Xăng – ti – mét vuông là diện tích của 1 hình vuông có cạnh là 1cm (viết tắt là cm²)

Ví dụ:

Năm xăng-ti-mét vuông: 5cm²

Một trăm hai mươi xăng-ti-mét vuông: 120cm²

4. Hình chữ nhật

4.1. Đặc điểm hình chữ nhật

Hình chữ nhật ABCD có:

- 4 góc đỉnh A, B, C, D đều là các góc vuông.

- 4 cạnh gồm: 2 cạnh dài là AB và CD; 2 cạnh ngắn là AD và BC

Hai cạnh có độ dài bằng nhau, viết là: AB = CD

Hai cạnh ngắn có độ dài bằng nhau, viết là: AD = BC

Hình chữ nhật có 4 góc vuông, có 2 cạnh dài bằng nhau và 2 cạnh ngắn bằng nhau.

Độ dài cạnh dài gọi là chiều dài, độ dài cạnh ngắn gọi là chiều rộng.

4.2. Chu vi hình chữ nhật

Quy tắc: Muốn tính chu vi hình chữ nhật ta lấy chiều dài cộng với chiều rộng (cùng đơn vị đo) rồi nhân với 2.

Ví dụ. Một mảnh đất hình chữ nhật có chiều dài 35m, chiều rộng 20m. Tính chu vi mảnh đất đó.

Bài giải

Chu vi mảnh đất hình chữ nhật là:

(35 + 20) × 2 = 110 (cm)

Đáp số: 110cm

4.3. Diện tích hình chữ nhật

Quy tắc: Muốn tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng đơn vị đo)

Ví dụ. Một miếng bìa hình chữ nhật có chiều rộng 5cm, chiều dài 14cm. Tính diện tích miếng bìa đó.

Bài giải

Diện tích miếng bìa hình chữ nhật là:

14 × 5 = 70 (cm²)

Đáp số: 70cm²

5. Hình vuông

5.1. Đặc điểm hình vuông

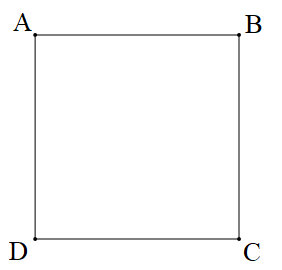
Hình vuông ABCD có:

- 4 góc đỉnh A, B, C, D đều là các góc vuông.

- 4 cạnh có độ dài bằng nhau: AB = BC = CD = DA

Hình vuông có 4 góc vuông và 4 cạnh bằng nhau.

5.2. Chu vi hình vuông

Quy tắc: Muốn tính chu vi hình vuông ta lấy độ dài một cạnh nhân với 4

Ví dụ. Người ta uốn một đoạn dây thép vừa đủ thành một hình vuông cạnh 10cm. Tính độ dài đoạn dây đó.

Bài giải

Độ dài đoạn dây chính là chu vi của hình vuông cạnh 10cm.

Độ dài đoạn dây đó là:

10 × 4 = 40 (cm)

Đáp số: 40cm

5.3. Diện tích hình vuông

Quy tắc: Muốn tính diện tích hình vuông ta lấy độ dài một cạnh nhân với chính nó.

Ví dụ. Một tờ giấy hình vuông cạnh 80mm. Tính diện tích tờ giấy đó theo xăng-ti-mét vuông.

Bài giải

Diện tích tờ giấy hình vuông là:

80 × 80 = 6400 (mm²)

Đổi: 6400mm² = 64cm²

Đáp số: 64cm²

Xem thêm các bài tổng hợp lý thuyết Toán lớp 3 đầy đủ, chi tiết khác:

Đọc, viết, so sánh các số có ba chữ số

Cộng trừ các số có ba chữ số (không nhớ)

Cộng các số có ba chữ số (có nhớ một lần)

Trừ các số có ba chữ số (có nhớ một lần)

Bảng nhân 6