Giải Toán 8 trang 22 Chân trời sáng tạo

Giải Toán 8 trang 22

Vận dụng 4 trang 22 Toán 8 Tập 1: Từ một khối lập phương có cạnh bằng 2x + 1, ta cắt bỏ một khối lập phương có cạnh bằng x + 1 (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

Lời giải:

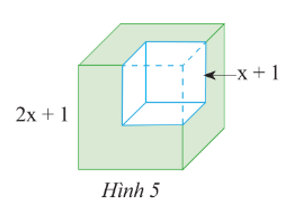
Thể tích của khối lập phương có cạnh bằng 2x + 1 là: (2x + 1)³.

Thể tích của khối lập phương có cạnh bằng x + 1 là: (x + 1)³.

Cách 1: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³ – (x³ + 3.x².1 + 3.x.1² + 1³)

= 8x³ + 12x² + 6x + 1 – x³ – 3x² – 3x – 1

= (8x³ –  x³) + (12x² – 3x²) + (6x – 3x) + (1 – 1)

= 7x³ + 9x² + 3x.

Cách 1: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= [(2x + 1) – (x + 1)].[(2x + 1)² + (2x + 1).(x + 1) + (x + 1)²]

= [2x + 1 – x – 1].[(2x)² + 2.2x.1 + 1² + (2x.x + 2x.x + 1.x + 1.1) + x² + 2.x.1 + 1²]

= x.[4x² + 4x + 1 + 2x² + 3x + 1 + x² + 2x + 1]

= x.[(4x² + 2x² + x²) + (4x + 3x + 2x) + (1 + 1 + 1)]

= x.[7x² + 9x + 3]

= 7x³ + 9x² + 3x.

Bài tập

Bài 1 trang 22 Toán 8 Tập 1: Tính:

a) (3x + 4)²;

b) (5x – y)²;

c) ${\left(xy-\frac{1}{2}y\right)}^2$.

Lời giải:

a) (3x + 4)²

= (3x)² + 2.3x.4 + 4²

= 9x² + 24x + 16.

b) (5x – y)²

= (5x)² – 2.5x.y + y²

= 25x² – 10xy + y².

c) ${\left(xy-\frac{1}{2}y\right)}^2$

$={\left(xy\right)}^2-2.xy.\frac{1}{2}y+{\left(\frac{1}{2}y\right)}^2$

$=x^2{y}^2-x{y}^2+\frac{1}{4}{y}^2$.

Bài 2 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) x² + 2x + 1;

b) 9 – 24x + 16x²;

c) 4x² + $\frac{1}{4}$ + 2x.

Lời giải:

a) x² + 2x + 1

= x² + 2.x.1 + 1²

= (x + 1)².

b) 9 – 24x + 16x²

= 3² – 2.3.4x + (4x)²

= (3 – 4x)².

Ta cũng có thể viết như sau:

9 – 24x + 16x²

= 16x² – 24x + 9

= (4x)² – 2.4x.3 + 3²

= (4x – 3)².

c) $4x^2+\frac{1}{4}+2x$

$=4x^2+2x+\frac{1}{4}$

$={\left(2x\right)}^2+2.2x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2$

$={\left(2x+\frac{1}{2}\right)}^2$.

Bài 3 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (3x – 5)(3x + 5);

b) (x – 2y)(x + 2y);

c) $\left(-x-\frac{1}{2}y\right)\left(-x+\frac{1}{2}y\right)$.

Lời giải:

a) (3x – 5)(3x + 5)

= (3x)² – 5²

= 9x² – 25.

b) (x – 2y)(x + 2y)

= x² – (2y)²

= x² – 4y².

c) $\left(-x-\frac{1}{2}y\right)\left(-x+\frac{1}{2}y\right)$

$={\left(-x\right)}^2-{\left(\frac{1}{2}y\right)}^2$

$=x^2-\frac{1}{4}{y}^2$.

Bài 4 trang 22 Toán 8 Tập 1:

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 dưới dạng đa thức.

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 dưới dạng đa thức.

Lời giải:

a) Biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 là:

(2x + 3)² = (2x)² + 2.2x.3 + 3² = 4x² + 12x + 9.

b) Biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 là:

(3x – 2)³ = (3x)³ – 3.(3x)².2 + 3.3x.2² – 2³

               = 27x³ – 54x² + 36x – 8.

Bài 5 trang 22 Toán 8 Tập 1: Tính nhanh:

a) 38 . 42;

b) 102²;

c) 198²;

d) 75² – 25².

Lời giải:

a) 38 . 42 = (40 – 2).(40 + 2) = 40² – 2² = 1 600 – 4 = 1 596.

b) 102² = (100 + 2)² = 100² + 2.100.2 + 2² = 10 000 + 400 + 4 = 10 404.

c) 198² = (200 – 2)² = 200² – 2.200.2 + 2² = 40 000 – 800 + 4 = 39 204.

d) 75² – 25² = (75 + 25).(75 – 25) = 100 . 50 = 5 000.

Bài 6 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (2x – 3)³;

b) (a + 3b)³;

c) (xy –1)³.

Lời giải:

a) (2x – 3)³

= (2x)³ – 3.(2x)².3 + 3.2x.3² – 3³

= 8x³ – 36x² + 54x – 8.

b) (a + 3b)³

= a³ + 3.a².3b + 3.a.(3b)² + (3b)³

= a³ + 9a²b + 27ab² + 27b³.

c) (xy –1)³

= (xy)³ – 3.(xy)².1 + 3.xy.1² – 1³

= x³y³ – 3x²y² + 3xy – 1.

Bài 7 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (a – 5)(a² + 5a + 25);

b) (x + 2y)(x² – 2xy + 4y²).

Lời giải:

a) (a – 5)(a² + 5a + 25)

= (a – 5)(a² + a.5 + 5²)

= a³ – 5³

= a³ – 125.

b) (x + 2y)(x² – 2xy + 4y²)

= (x + 2y).[x² – x.2y + (2y)²]

= x³ + (2y)³

= x³ + 8y³.

Bài 8 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (a – 1)(a + 1)(a² + 1);

b) (xy + 1)² – (xy – 1)².

Lời giải:

a) (a – 1)(a + 1)(a² + 1)

= (a² – 1)(a² + 1)

= (a²)² – 1²

= a⁴ – 1.

b) (xy + 1)² – (xy – 1)²

= [(xy + 1) + (xy – 1)].[(xy + 1) – (xy – 1)]

= [xy + 1 + xy – 1].[xy + 1 – xy + 1]

= 2xy.2

= 4xy.

Bài 9 trang 22 Toán 8 Tập 1:

a) Cho x + y = 12 và xy = 35. Tính (x − y)².

b) Cho x – y = 8 và xy = 20. Tính (x + y)².

c) Cho x + y = 5 và xy = 6. Tính x³ + y³.

d) Cho x – y = 3 và xy = 40. Tính x³ – y³.

Lời giải:

a) Ta có: (x − y)² = x² – 2xy + y²

                           = x² + 2xy + y² – 4xy

                           = (x + y)² – 4xy

Thay x + y = 12 và xy = 35 vào biểu thức trên ta có:

(x − y)² = 12² – 4.35 = 144 – 140 = 4.

b) Ta có: (x + y)² = x² + 2xy + y²

                           = x² – 2xy + y² + 4xy

                           = (x – y)² + 4xy

Thay x – y = 8 và xy = 20 vào biểu thức trên ta có:

(x + y)² = 8² + 4.20 = 64 + 80 = 144.

c) Ta có: x³ + y³ = (x + y).(x² – xy + y²)

                           = (x + y).(x² + 2xy + y² – 3xy)

                           = (x + y).[(x + y)² – 3xy]

Thay x + y = 5 và xy = 6 vào biểu thức trên ta có:

x³ + y³ = 5.(5² – 3.6) = 5.(25 – 18) = 5.7 = 35.

d) Ta có: x³ – y³ = (x – y).(x² + xy + y²)

                           = (x – y).(x² – 2xy + y² + 3xy)

                           = (x – y).[(x – y)² + 3xy]

Thay x – y = 3 và xy = 40 vào biểu thức trên ta có:

x³ – y³ = 3.(3² – 3.40) = 3.(9 – 120) = 5.(–111) = –555.

Bài 10 trang 22 Toán 8 Tập 1: Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm a cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm a cm?

Lời giải:

Thể tích hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm là:

5³ = 125 (cm³).

a) Chiều dài của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Chiều rộng của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).5 = (5 + a)².5

                          = (5² + 2.5.a + a²).5

                          = (25 + 10a + a²).5

                          = 25.5 + 10a.5 + a².5

                          = 125 + 50a + 5a² (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 50a + 5a² – 125 = 5a² + 50a (cm³).

b) Chiều cao của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).(5 + a) = (5 + a)³

                                   = 5³ + 3.5².a + 3.5.a² + a³

                                   = 125 + 75a + 15a² + a³ (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 75a + 15a² + a³ – 125 = a³ + 15a² + 75a (cm³).

Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

Giải Toán 8 trang 18

Giải Toán 8 trang 19

Giải Toán 8 trang 20

Giải Toán 8 trang 21

Giải Toán 8 trang 22