Giải Toán 12 trang 38 Tập 1 Chân trời sáng tạo

Giải Toán 12 trang 38 Tập 1

Bài 8 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{-2x-3}{4-x}$. Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên (– ∞; – 4) và nghịch biến trên (– 4; + ∞).

B. Hàm số đồng biến trên (– ∞; 4) và (4; + ∞).

C. Hàm số nghịch biến trên (– ∞; 4) và (4; + ∞).

D. Hàm số nghịch biến trên (– ∞; – 4) và (– 4; + ∞).

Lời giải:

Đáp án đúng là: C

Xét hàm số $y=\frac{-2x-3}{4-x}$.

Tập xác định: D = ℝ\{4}.

Đạo hàm $y^{\text{'}}=\frac{-5}{{\left(4-x\right)}^2}$. Vì y' < 0 với mọi x ≠ 4 nên hàm số nghịch biến trên mỗi khoảng (– ∞; 4) và (4; + ∞).

Bài tập tự luận

Bài 9 trang 38 Toán 12 Tập 1: Tìm hai số không âm a và b có tổng bằng 10 sao cho:

a) Biểu thức ab đạt giá trị lớn nhất;

b) Tổng các bình phương của chúng đạt giá trị nhỏ nhất;

c) Biểu thức ab² đạt giá trị lớn nhất.

Lời giải:

Ta có a + b = 10, suy ra b = 10 – a.

Vì a, b ≥ 0 nên 10 – a ≥ 0, suy ra a ≤ 10.

a) Ta có ab = a(10 – a) = – a² + 10a.

Xét hàm số H(a) = – a² + 10a với a ∈ [0; 10].

Đạo hàm H'(a) = – 2a + 10. Trên khoảng (0; 10), H'(a) = 0 khi a = 5.

H(0) = 0; H(5) = 25; H(10) = 0.

Do đó, $\underset{\left[0;10\right]}{\max }H\left(a\right)=25$ tại a = 5.

Với a = 5 thì b = 10 – 5 = 5.

Vậy biểu thức ab đạt giá trị lớn nhất bằng 25 khi a = b = 5.

b) Ta có a² + b² = a² + (10 – a)² = 2a² – 20a + 100.

Xét hàm số S(a) = 2a² – 20a + 100 với a ∈ [0; 10].

Đạo hàm S'(a) = 4a – 20. Trên khoảng (0; 10), S'(a) = 0 khi a = 5.

S(0) = 100; S(5) = 50; S(10) = 100.

Do đó, $\underset{\left[0;10\right]}{\min }S\left(a\right)=50$ tại a = 5.

Vậy tổng các bình phương của hai số a và b đạt giá trị nhỏ nhất bằng 50 khi a = b = 5.

c) Ta có ab² = a(10 – a)² = a³ – 20a² + 100a.

Xét hàm số T(a) = a³ – 20a² + 100a với với a ∈ [0; 10].

Đạo hàm T'(a) = 3a² – 40a + 100. Trên khoảng (0; 10), S'(a) = 0 khi a = $\frac{10}{3}$.

T(0) = 0; $T\left(\frac{10}{3}\right)=\frac{4000}{27}$; T(10) = 0.

Do đó, $\underset{\left[0;10\right]}{\max }T\left(a\right)=\frac{4000}{27}$ tại a = $\frac{10}{3}$.

Với a = $\frac{10}{3}$ thì $b=10-\frac{10}{3}=\frac{20}{3}$.

Vậy biểu thức ab² đạt giá trị lớn nhất bằng $\frac{4000}{3}$ tại $a=\frac{10}{3},b=\frac{20}{3}$.

Bài 10 trang 38 Toán 12 Tập 1: Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.

Lời giải:

Giả sử hàm số bậc ba cần tìm có dạng y = f(x) = ax³ + bx² + cx + d (a ≠ 0).

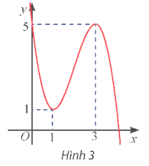
Quan sát Hình 3, ta thấy đồ thị hàm số đi qua các điểm (0; 5), (1; 1) và (3; 5).

Với x = 0 thì y = 5, thay vào hàm số ta suy ra d = 5.

Khi đó hàm số trở thành y = f(x) = ax³ + bx² + cx + 5.

Với x = 1 thì y = 1, thay vào hàm số ta được a + b + c + 5 = 1 (1).

Ta thấy đồ thị hàm số có hai điểm cực trị là (1; 1) và (3; 5), tức là phương trình y' = 0 có hai nghiệm là x = 1 và x = 3.

Ta có y' = 3ax² + 2bx + c.

Với x = 1 thì y' = 0 nên ta có 3a + 2b + c = 0 (2).

Với x = 3 thì y' = 0 nên ta có 27a + 6b + c = 0 (3).

Từ (1), (2) và (3) ta suy ra a = – 1; b = 6; c = – 9.

Vậy hàm số cần tìm là y = f(x) = – x³ + 6x² – 9x + 5.

Bài 11 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{1}{3}{x}^3-x^2+4$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.

Lời giải:

a) Xét hàm số $y=\frac{1}{3}{x}^3-x^2+4$.

1. Tập xác định: ℝ.

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = x² – 2x; y' = 0 ⇔ x = 0 hoặc x = 2.

Trên các khoảng (– ∞; 0) và (2; + ∞), y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên khoảng (0; 2), y' < 0 nên hàm số nghịch biến trên khoảng đó.

● Cực trị:

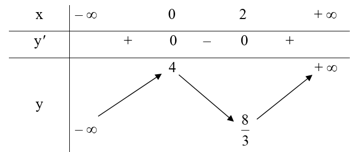
Hàm số đạt cực đại tại x = 0 và y_CĐ = 4.

Hàm số đạt cực tiểu tại x = 2 và y_CT = $\frac{8}{3}$.

● Các giới hạn tại vô cực:

$\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }{x}^3\left(\frac{1}{3}-\frac{1}{x}+\frac{4}{x^3}\right)=-\infty ;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }{x}^3\left(\frac{1}{3}-\frac{1}{x}+\frac{4}{x^3}\right)=+\infty$

Ÿ Bảng biến thiên:

3. Đồ thị:

Khi x = 0 thì y = 4 nên (0; 4) là giao điểm của đồ thị với trục Oy.

Ta có y = 0 ⇔ $\frac{1}{3}{x}^3-x^2+4$ = 0, phương trình này có 1 nghiệm nên đồ thị của hàm số giao với trục Ox tại 1 điểm.

Điểm (0; 4) là cực đại và điểm $\left(2;\frac{8}{3}\right)$ là điểm cực tiểu của đồ thị hàm số.

Đồ thị hàm số đi qua điểm (3; 4).

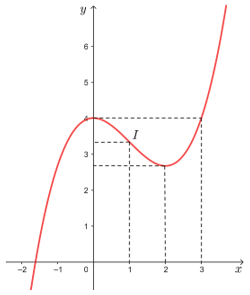
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Đồ thị của hàm số có tâm đối xứng là điểm I$\left(1;\frac{10}{3}\right)$.

b) Hai điểm cực trị của đồ thị hàm số là (0; 4) và $\left(2;\frac{8}{3}\right)$.

Khoảng cách giữa hai điểm cực trị của đồ thị hàm số là

$d=\sqrt{{\left(2-0\right)}^2+{\left(\frac{8}{3}-4\right)}^2}=\frac{4\sqrt{10}}{3}$.

Bài 12 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{2x+1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.

Lời giải:

a) Xét hàm số $y=\frac{2x+1}{x-1}$.

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = $\frac{-3}{{\left(x-1\right)}^2}$. Vì y' < 0 với mọi x ≠ 1 nên hàm số nghịch biến trên mỗi khoảng (– ∞; 1) và (1; + ∞).

● Tiệm cận:

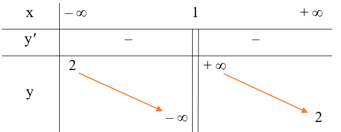
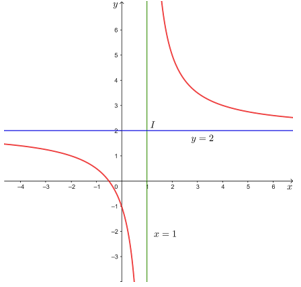
Ta có $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x+1}{x-1}=2;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x+1}{x-1}=2$. Suy ra đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Ta có $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{2x+1}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{2x+1}{x-1}=+\infty$. Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

● Bảng biến thiên:

3. Đồ thị:

Với x = 0 thì y = – 1 nên đồ thị hàm số giao với trục Oy tại điểm (0; – 1).

Với y = 0 thì x = $-\frac{1}{2}$ nên đồ thị hàm số giao với trục Ox tại điểm $\left(-\frac{1}{2};0\right)$.

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là điểm I(1; 2). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = 2.

b) Ta có A(0; – 1), I(1; 2).

Vì B đối xứng với A qua I nên I là trung điểm của AB.

Khi đó, tọa độ của điểm B là $\left\{\begin{array}{l}{x}_B=2x_I-x_A=2\cdot 1-0=2\\ y_B=2y_I-y_A=2\cdot 2-\left(-1\right)=5\end{array}\right.$. Suy ra B(2; 5).

Ta có $\frac{2\cdot 2+1}{2-1}=5$, do đó điểm B(2; 5) thuộc đồ thị hàm số $y=\frac{2x+1}{x-1}$.

Bài 13 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+4x-1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].

Lời giải:

a) Xét hàm số $y=\frac{x^2+4x-1}{x-1}$.

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = $\frac{x^2-2x-3}{{\left(x-1\right)}^2}$. Ta có y' = 0 ⇔ x = – 1 hoặc x = 3.

Trên các khoảng (– ∞; – 1) và (3; + ∞), y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên các khoảng (– 1; 1) và (1; 3), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

● Cực trị:

Hàm số đạt cực tiểu tại x = 3 và y_CT = 10.

Hàm số đạt cực đại tại x = – 1 và y­_CĐ = 2.

● Các giới hạn tại vô cực và tiệm cận:

$\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{x^2+4x-1}{x-1}=-\infty ;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{x^2+4x-1}{x-1}=+\infty$

Ta có $a=\underset{x\to +\infty }{\lim }\frac{x^2+4x-1}{x\left(x-1\right)}=1$ và $b=\underset{x\to +\infty }{\lim }\left(\frac{x^2+4x-1}{x-1}-x\right)=\underset{x\to +\infty }{\lim }\frac{5x-1}{x-1}=5$.

Suy ra đường thẳng y = x + 5 là tiệm cận xiên của đồ thị hàm số.

Ta có $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{x^2+4x-1}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{x^2+4x-1}{x-1}=+\infty$. Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

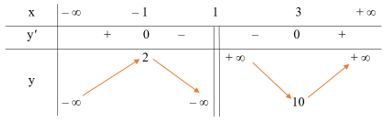
● Bảng biến thiên:

3. Đồ thị:

Ta có y = 0 ⇔ $\frac{x^2+4x-1}{x-1}=0$ ⇔ x = $-2+\sqrt{5}$ hoặc x = $-2-\sqrt{5}$.

Vậy đồ thị hàm số giao với trục Ox tại điểm $\left(-2-\sqrt{5};0\right)$ và điểm $\left(-2+\sqrt{5};0\right)$.

Đồ thị hàm số giao với trục Oy tại điểm (0; 1).

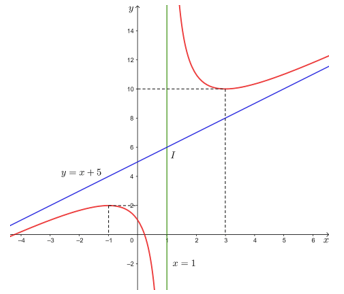
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là điểm I(1; 6).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = x + 5.

b) Xét hàm số $y=\frac{x^2+4x-1}{x-1}$ với x ∈ [2; 4].

Trên khoảng (2; 4), y' = 0 khi x = 3.

Ta có y(2) = 11; y(3) = 10; y(4) = $\frac{31}{3}$.

Vậy $\underset{\left[2;4\right]}{\max }y=11$ tại x = 2 và $\underset{\left[2;4\right]}{\min }y=10$ tại x = 3.

Bài 14 trang 38 Toán 12 Tập 1: Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

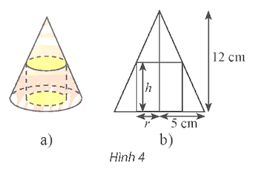
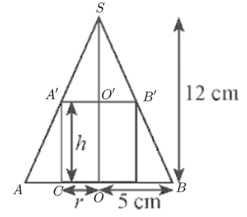
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: $r=\frac{5\left(12-h\right)}{12}$.

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Tìm h để khối trụ có thể tích lớn nhất.

Lời giải:

a) Ta đặt tên các điểm như hình vẽ dưới đây:

Ta có A'O' // AO nên $\frac{S{O}^{\text{'}}}{SO}=\frac{S{A}^{\text{'}}}{SA}$.

Lại có A'C // SO nên $\frac{S{A}^{\text{'}}}{SA}=\frac{OC}{OA}$.

Từ đó suy ra $\frac{S{O}^{\text{'}}}{SO}=\frac{OC}{OA}$.

Mà SO = 12 cm, OA = 5 cm, OC = r, SO' = SO – OO' = 12 – h.

Do đó, $\frac{12-h}{12}=\frac{r}{5}$. Suy ra $r=\frac{5\left(12-h\right)}{12}$.

b) Thể tích của khối trụ là V = πr²h = $\pi \cdot {\left[\frac{5\left(12-h\right)}{12}\right]}^2\cdot h=\frac{25\pi h{\left(12-h\right)}^2}{144}$(cm³).

Vậy thể tích khối trụ theo h là $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Rõ ràng h phải thỏa mãn điều kiện 0 < h < 12.

Xét hàm số $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$ với h ∈ (0; 12).

Ta có $V^{\text{'}}\left(h\right)=\frac{25\pi \left(12-h\right)\left(12-3h\right)}{144}$.

Trên khoảng (0; 12), ta có V'(h) = 0 khi h = 4.

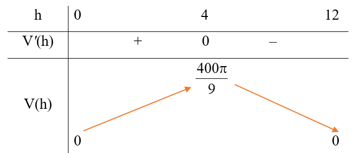
Bảng biến thiên:

Căn cứ vào bảng biến thiên, ta thấy trên khoảng (0; 12), hàm số V(h) đạt giá trị lớn nhất bằng $\frac{400\pi }{9}$ tại h = 4.

Vậy h = 4 cm thì khối trụ có thể tích lớn nhất.

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 12 trang 37 Tập 1

Giải Toán 12 trang 38 Tập 1

Giải Toán 12 trang 39 Tập 1