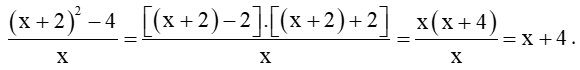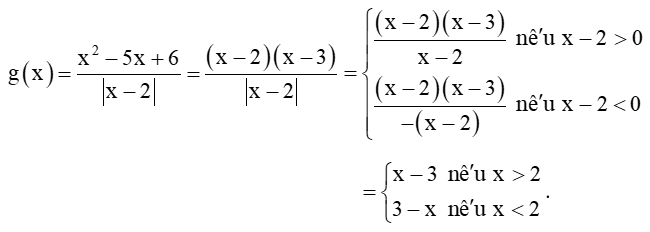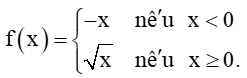Giải Toán 11 trang 118 Kết nối tri thức
Với giải bài tập Toán 11 trang 118 trong Bài 16: Giới hạn của hàm số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 118.
Giải Toán 11 trang 118
Luyện tập 5 trang 118 Toán 11 Tập 1: Tính limx→2+2x−1x−2 và limx→2−2x−1x−2.
Lời giải:
+) Ta có: limx→2+(x−2)=0, x – 2 > 0 với mọi x > 2 và
limx→2+(2x−1)=2.2−1=3>0.
Do đó, limx→2+2x−1x−2=+∞.
+) Ta có: limx→2−(x−2)=0, x – 2 < 0 với mọi x < 2 và
limx→2−(2x−1)=2.2−1=3>0.
Do đó, limx→2−2x−1x−2=−∞.
Bài tập
Lời giải:
+) Biểu thức f(x) có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1.
Ta có: f(x)=x2−1x−1=(x−1)(x+1)x−1=x+1, với mọi x ≠ 1.
Biểu thức g(x) = x + 1 có nghĩa với mọi x.
Do đó, điều kiện xác định của hai hàm số f(x) và g(x) khác nhau, vậy khẳng định a) là sai.
+) Ta có: limx→1f(x)=limx→1x2−1x−1=limx→1(x+1)=1+1=2;
limx→1g(x)=limx→1(x+1)=1+1=2.
Vậy limx→1f(x)=limx→1g(x) nên khẳng định b) là đúng.
Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau:
Lời giải:
Do mẫu thức có giới hạn là 0 khi x ⟶ 0 nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số đối với cả hai câu a và b.
a) Ta có:
Do đó limx→0(x+2)2−4x=limx→0(x+4)=0+4=4.
b) Ta có: √x2+9−3x2=(√x2+9)2−32x2(√x2+9+3)=x2x2(√x2+9+3)=1√x2+9+3.
Do đó limx→0√x2+9−3x2=limx→01√x2+9+3=16.
Tính limt→0+H(t) và limt→0−H(t).
Lời giải:
Với dãy số (tn) bất kì sao cho tn < 0 và tn ⟶ 0, ta có H(tn) = 0.
Do đó limt→0−H(t)=limn→+∞H(tn)=limn→+∞0=0.
Tương tự, với dãy số (tn) bất kì sao cho tn > 0 và tn ⟶ 0, ta có H(tn) = 1.
Do đó limt→0+H(t)=limn→+∞H(tn)=limn→+∞1=1.
Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên:
Lời giải:
a) Ta có: limx→1+(x−1)=0, x – 1 > 0 với mọi x > 1 và
limx→1+(x−2)=1−2=−1<0.
Do đó, limx→1+x−2x−1=−∞.
b) Ta có: limx→4−(4−x)=0, 4 – x > 0 với mọi x < 4 và
limx→4−(x2−x+1)=42−4+1=13>0.
Do đó, limx→4−x2−x+14−x=+∞.
Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số 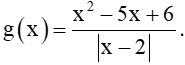
Tìm limx→2+g(x) và limx→2−g(x).
Lời giải:
Ta có:
Do đó, limx→2+g(x)=limx→2+(x−3)=2−3=−1;
limx→2−g(x)=limx→2−(3−x)=3−2=1.
Bài 5.12 trang 118 Toán 11 Tập 1:Tính các giới hạn sau:
Lời giải:
a)limx→+∞1−2x√x2+1=limx→+∞1−2x√x2(1+1x2)=limx→+∞x(1x−2)x√1+1x2=limx→+∞1x−2√1+1x2=−2√1=−2.
b) Ta có: √x2+x+2−x=(√x2+x+2)2−x2√x2+x+2+x=x+2√x2+x+2+x
Do đó, limx→+∞(√x2+x+2−x)=limx→+∞x+2√x2+x+2+x
=limx→+∞x+2√x2(1+1x+2x2)+x=limx→+∞x+2x√1+1x+2x2+x
=limx→+∞x(1+2x)x(√1+1x+2x2+1)=limx→+∞1+2x√1+1x+2x2+1=12
Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số f(x)=2(x−1)(x−2).
Tính limx→2+f(x) và limx→2−f(x).
Lời giải:
Ta có: f(x)=2(x−1)(x−2)=2x−1⋅1x−2
+) limx→2+2x−1=22−1=2>0 và limx→2+1x−2=+∞ (do x – 2 > 0 khi x > 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được limx→2+f(x)=limx→2+2(x−1)(x−2)=+∞.
+) limx→2−2x−1=22−1=2>0 và limx→2−1x−2=−∞ (do x – 2 < 0 khi x < 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được limx→2−f(x)=limx→2−2(x−1)(x−2)=−∞.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm. Cho hàm số f(x)=4−x2x−2...
Luyện tập 1 trang 113 Toán 11 Tập 1: Tính limx→1x−1√x−1...
HĐ2 trang 113 Toán 11 Tập 1: Nhận biết khái niệm giới hạn một bên. Cho hàm số 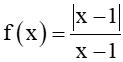
Luyện tập 2 trang 113 Toán 11 Tập 1: Cho hàm số
Tính limx→0+f(x), limx→0−f(x) và limx→0f(x)...
HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực. Cho hàm số f(x)=1+2x−1 có đồ thị như Hình 5.4...
Luyện tập 3 trang 115 Toán 11 Tập 1: Tính limx→+∞√x2+2x+1...
HĐ4 trang 115 Toán 11 Tập 1: Nhận biết khái niệm giới hạn vô cực. Xét hàm số f(x)=1x2 có đồ thị như Hình 5.6...
Luyện tập 4 trang 116 Toán 11 Tập 1: Tính các giới hạn sau: a) 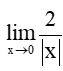
Luyện tập 5 trang 118 Toán 11 Tập 1: Tính và ...
Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số và g(x) = x + 1. Khẳng định nào sau đây là đúng...
Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau: a) ;...
Bài 5.9 trang 118 Toán 11 Tập 1: Cho hàm số 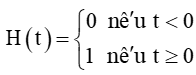
Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên: a) ;...
Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số 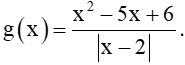
Bài 5.12 trang 118 Toán 11 Tập 1:Tính các giới hạn sau: a) ;...
Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số . Tính và ...
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức