Hoạt động 2 trang 59 Toán 10 Tập 2 | Cánh diều Giải Toán lớp 10
Lời giải Hoạt động 2 trang 59 Toán 10 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán 10 Cánh diều Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng
Hoạt động 2 trang 59 Toán 10 Tập 2: Mỗi nhóm thực hành xây dựng mô hình toán học dạng hàm số bậc nhất hoặc hàm số bậc hai để biểu diễn số liệu ở bảng thống kê theo các bước đã nêu ở mục I.2.
Lời giải
Theo đề tài ở hoạt động 1, ta xây dựng mô hình toán học dạng hàm số bậc nhất như sau:
Bước 1. Lựa chọn cách biểu diễn dữ liệu trên mặt phẳng tọa độ.
Đặt x = t – 2017 với t ∈ {2017, 2018, 2019, 2020}. Do đó ta có x ∈ {0; 1; 2; 3}.
Từ bảng ở hoạt động 1, ta có bảng thống kê như sau:
|
x |
0 |
1 |
2 |
3 |
|
Tỉ lệ sinh (%) |
1,98 |
1,98 |
1,98 |
2,06 |
Xét các điểm A(0; 1,98), B(1; 1,98), C(2; 1,98), D(3; 2,06) trong mặt phẳng tọa độ.
Bước 2. Xem tỉ lệ sinh mỗi năm f(x) là hàm số của x. Ta phải chọn f(x) là hàm số bậc nhất sao cho f(x) dự đoán (càng chính xác càng tốt) nhiệt độ ở những năm sau năm 2020, tức là tính được giá trị của f(x) với x ≥ 4.
Căn cứ vào bốn điểm A(0; 1,98), B(1; 1,98), C(2; 1,98), D(3; 2,06) ta chọn hàm số bậc nhất y = f(x) có đồ thị “gần” nhất với bốn điểm trên.
Thông thường việc tính toán trực tiếp để xác định được công thức của hàm số bậc nhất nói trên là không dễ dàng. Người ta dùng các phần mềm toán học để trợ giúp cho quá trình tính toán. Chẳng hạn, ta sử dụng phần mềm GeoGebra để xác định hàm số bậc nhất nói trên như sau:
Vào phần mềm GeoGebra, xuất diện giao diện như hình sau:
- Vẽ điểm A(0; 1,98) bằng cách dùng câu lệnh “=(0, 1.98)”, ta được như hình sau
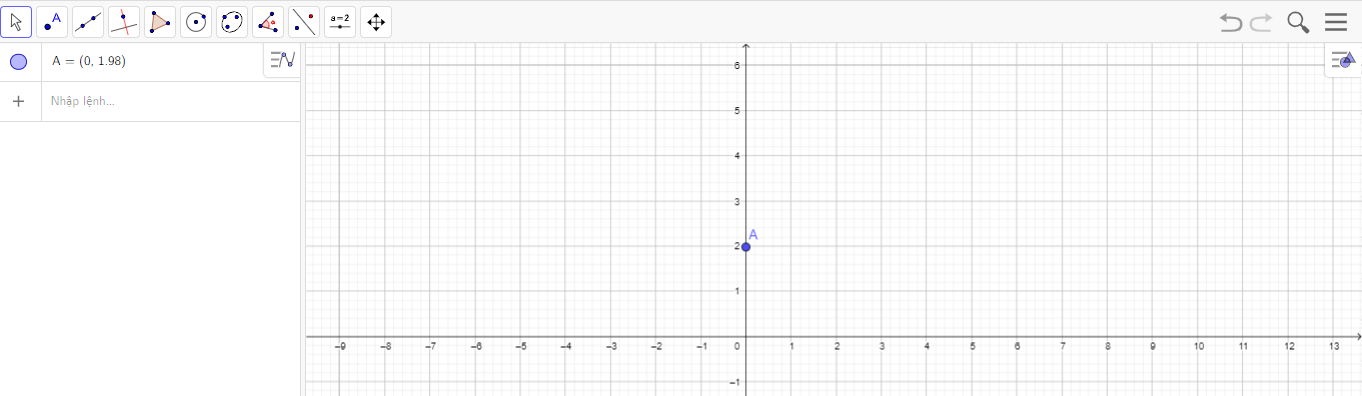
- Tương tự, vẽ các điểm B(1; 1,98), C(2; 1,98) và D(3; 2,06) trong mặt phẳng tọa độ bằng cách dùng các câu lệnh: “=(1, 1.98)”; “=(2, 1.98)”; “=(3, 2.06)”, ta được như hình sau:
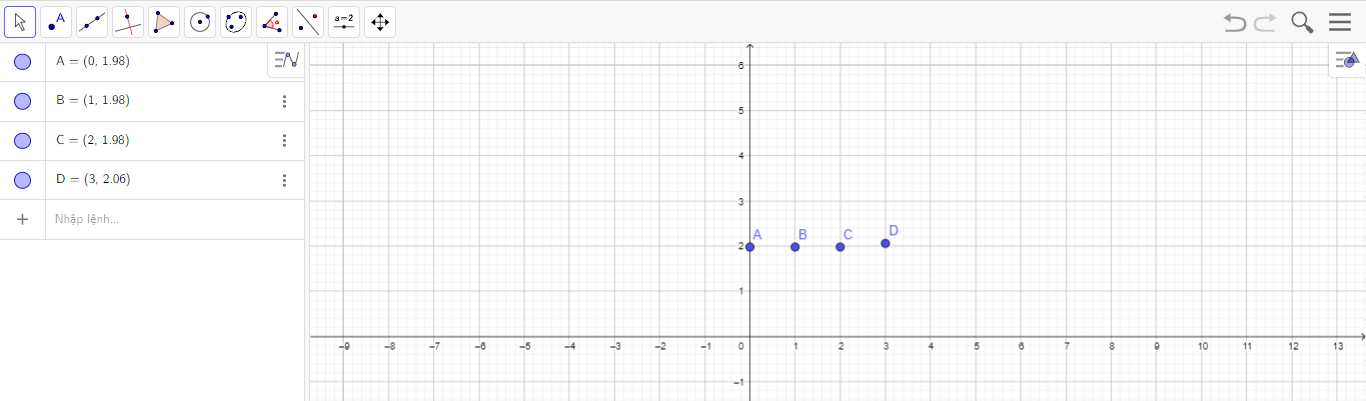
- Sử dụng câu lệnh:
“=FitPoly({A,B,C,D},1)” như hình sau:

ta được hàm: f(x) = 1,04x + 19,4 với đồ thị ở hình sau:
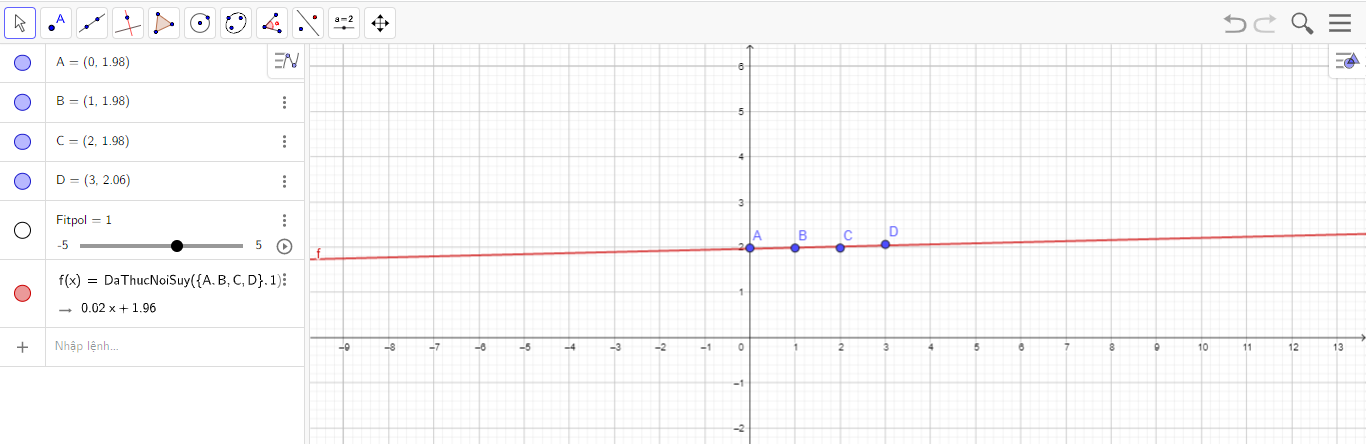
Bước 3. Dựa theo mô hình hàm số bậc nhất f(x) = 0,02x + 1,96, ta dự đoán được tỉ lệ sinh của các năm 2021, 2022, 2023... lần lượt là:
f(4) = 0,02 . 4 + 1,96 = 2,04;
f(5) = 0,02 . 5 + 1,96 = 2,06;
f(6) = 0,02 . 6 + 1,96 = 2,08.
Bước 4. Dự đoán trên là hợp lí, vì thế ta không cần điều chỉnh mô hình toán học đã chọn.
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Tập hợp. Các phép toán trên tập hợp
Bài tập cuối chương 1 trang 19
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều
