Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án)
Trắc nghiệm Toán 11 Bài 4: Hai mặt phẳng vuông góc
-
545 lượt thi
-
27 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
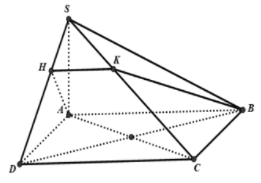
Dựng AH⊥CD
Ta có CD⊥SACD⊥AD}⇒CD⊥(SAD).
Suy ra CD⊥AH
mà AH⊂(SCD) suy ra AH⊂(α)
Do đó (α)≡(AHB)
Vì (α)//CD nên
(α)∩(SAD)=HK//CD(K∈SC).
Từ đó thiết diện là hình thang ABKH.
Mặt khác AB⊥(SAD) nên AB⊥AH
Vậy thiết diện là hình thang vuông tại A và H.
Câu 2:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Gọi MN là đoạn thẳng qua O vuông góc AD ( M,N thuộc AD,BC ) ta có
MN⊥ nên SMN là thiết diện cần tìm.
vuông tại M nên
Câu 5:
23/07/2024 Xem đáp án
Xem đáp án
Câu 7:
19/11/2024 Xem đáp án
Xem đáp án
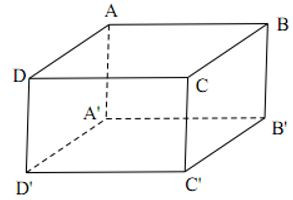
- Định nghĩa: Hình hộp chữ nhật là hình không gian có 6 mặt đều là những hình chữ nhật.
+ Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
+ Hai mặt không có cạnh chung gọi là hai mặt đối diện và có thể xem chúng là mặt đáy của hình hộp chữ nhật, các mặt còn lại được gọi là mặt bên.
Câu 8:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Theo Định lí .
Câu 9:
23/07/2024Cho hai mặt phẳng và vuông góc với nhau và gọi .
I. Nếu và thì .
II. Nếu thì .
III. Nếu b d thì b hoặc b ().
IV. Nếu thì và
Các mệnh đề đúng là:
 Xem đáp án
Xem đáp án
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Gọi nếu thì .
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Qua M dựng đường thẳng vuông cóc với và . Khi đó có vô số mặt phẳng xoay quanh thỏa yêu cầu bài toán.
Câu 14:
22/11/2024 Xem đáp án
Xem đáp án
Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì hoặc song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.
*Phương pháp giải:
Dụa vào tính chất 2 mặp phẳng vuông góc
*Lý thuyết:
1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc
- Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a, b tương ứng vuông góc với (P), (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a, b và được gọi là góc giữa hai mặt phẳng (P) và (Q).
- Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng .
Chú ý: Nếu là góc giữa hai mặt phẳng (P) và (Q) thì .
Nhận xét:
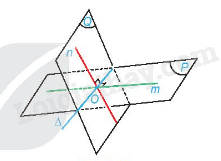
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Lấy hai đường thẳng m, n tương ứng thuộc (P), (Q) và cùng vuông góc với tại một điểm O (nói cách khác, lấy một mặt phẳng vuông góc với , cắt (P), (Q) tương ứng theo các giao tuyến m, n). Khi đó, góc giữa (P) và (Q) bằng góc giữa m và n. Đặc biệt, (P) vuông góc với (Q) khi và chỉ khi m vuông góc với n.
2. Điều kiện để hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
3. Tính chất của hai mặt phẳng vuông góc
- Với hai mặt phẳng vuông góc với nhau, bất kì đường thẳng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
Nhận xét: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Mỗi đường thẳng qua điểm O thuộc (P) và vuông góc với mặt phẳng (Q) thì đường thẳng đó thuộc mặt phẳng (P).
- Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
4. Góc nhị diện
- Hình gồm hai nửa mặt phẳng (P), (Q) có chung bờ a được gọi là một góc nhị diện, kí hiệu là [P,a,Q]. Đường thẳng a và các nửa mặt phẳng (P), (Q) tương ứng được gọi là cạnh và các mặt của góc nhị diện đó.
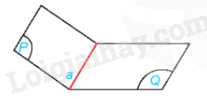
Mỗi đường thẳng a trong một mặt phẳng chia mặt phẳng thành hai phần, mỗi phần cùng với a là một nửa mặt phẳng bờ a.
- Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P,a,Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P,a,Q] (gọi tắt là góc phẳng nhị diện). Số đo của góc xOy không phụ thuộc vào vị trí của O trên a, được gọi là số đo của góc nhị diện [P,a,Q].
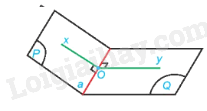
Mặt phẳng chứa góc phẳng nhị diện xOy của [P,a,Q] vuông góc với cạnh a.
Chú ý:
- Số đo của góc nhị diện có thể nhận giá trị từ đến . Góc nhị diện được gọi là góc vuông, nhọn, tù nếu nó có số đo tương ứng bằng, nhỏ hơn, lớn hớn .
- Đối với hai điểm M, N không thuộc đường thẳng a, ta kí hiệu [M, a, N] là góc nhị diện có cạnh a và các mặt tương ứng chứa M, N.
- Hai mặt phẳng cắt nhau tạo thành bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì các góc nhị diện còn lại cũng là góc nhị diện vuông.
Xem thêm
Lý thuyết Hai mặt phẳng vuông góc – Toán 11 Kết nối tri thứcCâu 15:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
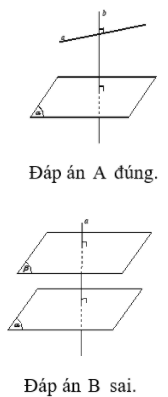
Câu 16:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
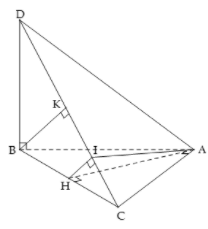
Ta có:
Gọi H là trung điểm BC, ta có
Trong mặt phẳng , kẻ thì ta có
Khi đó mặt phẳng cắt tứ diện ABCD theo thiết diện là tam giác AHI
Mặt khác tam giác ABC vuông cân tại A nên .
Trong tam giác vuông BCD, kẻ đường cao BK thì và
Vậy: thiết diện cần tìm là tam giác AHI vuông tại H và có diện tích
Câu 17:
11/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Lời giải:
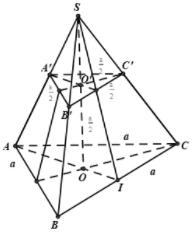
+ Đáp án A đúng.
+ Gọi I là trung điểm của BC.
Từ giả thiết dễ dàng chỉ ra được
. Mặt khác là tam giác đều cạnh a, có AI là đường trung tuyến
Áp dụng định lý Pytago trong vuông tại O ta có:
Vì là hình chóp cụt đều nên
đáp án B sai.
+ Ta có: .
Vì cân tại S và I là trung điểm của BC nên suy ra .
Mặt khác là tam giác đều có I là trung điểm của BC
đáp án C đúng.
+ Ta có:
đáp án D đúng.
*Phương pháp giải:
Sử dụng định lí pytago tinh phần b
*Lý thuyết:
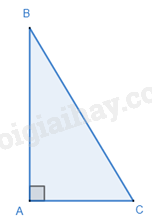
1. Định lí Pythagore
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
2. Định lí Pythagore đảo
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
Xem thêm
Lý thuyết Định lí Pythagore – Toán lớp 8 Chân trời sáng tạoCâu 18:
11/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Lời giải:
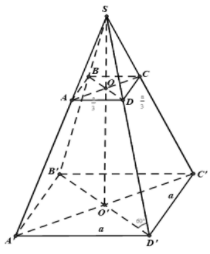
Ta có
là hình chiếu vuông góc của lên .
Từ giả thiết dễ dàng chỉ ra được
Vì là tam giác vuông cân tại có là đường cao nên ta có:
Áp dụng hệ thức lượng trong vuông tại ta có:
*Phương pháp giải:
Sử dụng cộng thức tính đường cao trong tam giác
Áp dụng hệ thực lượng trong tam giác
*Lý thuyết:
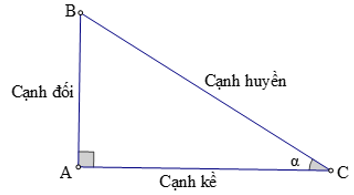
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cos α.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tan α.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cot α.
Xem thêm
200 bài tập hệ thức lượng nâng cao (2024) có đáp ánCâu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
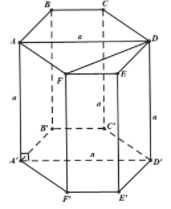
Tổng số đo các góc của hình lục giác là . Vì là hình lục giác đều nên mỗi góc của hình lục giác đều là
. Vì là hình lục giác đều nên ta suy ra:
+ AD là tia phân giác của góc và
+ Tam giác AFD vuông tại F.
Xét tam giác AFD vuông tại F có và ta suy ra:
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
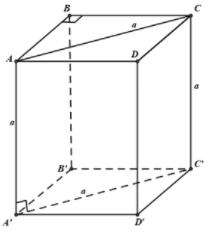
Từ giả thiết ta suy ra vuông cân tại B
Áp dụng hệ thức lượng trong vuông cân tại B có và cạnh , ta có:
Câu 21:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
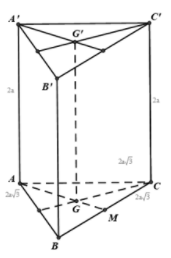
Gọi M là trung điểm BC. Khi đó ta dễ dàng tính được:
Vì G là trọng tâm tam giác ABC nên:
là hình vuông có cạnh bằng 2a.
Câu 22:
25/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Lời giải:
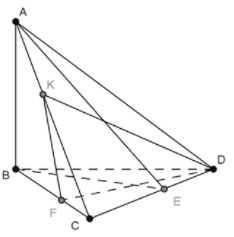
Ta có:
Mặt khác:
nên câu A đúng.
nên câu C đúng.
Theo trên ta có nên .
Vậy ta có
.
*Phương pháp giải:
Sử dụng cách chứng minh hai mặt phẳng vuông góc
- Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).
*Lý thuyết:
1. Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng và là góc giữa hai đường thẳng lần lượt vuông góc với và , kí hiệu .
Ta có: với .
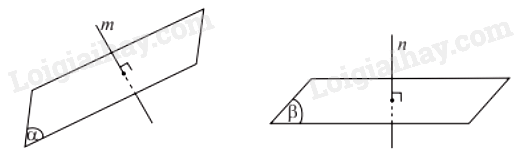
2. Hai mặt phẳng vuông góc
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là một góc vuông.
Hai mặt phẳng (P) và (Q) vuông góc được kí hiệu là .
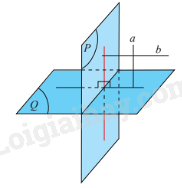
3. Điều kiện để hai mặt phẳng vuông góc
Định lí 1:
Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
4. Tính chất cơ bản về hai mặt phẳng vuông góc
Định lí 2:
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
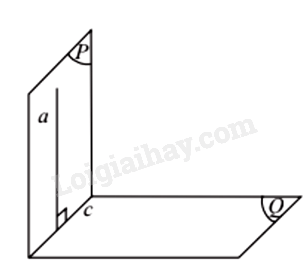
Định lí 3:
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
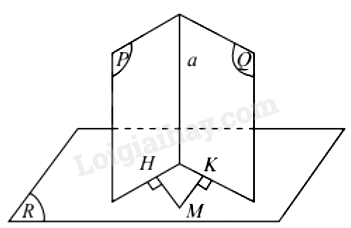
Xem thêm
Cách chứng minh 2 mặt phẳng vuông gócCâu 23:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
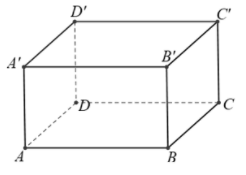
Câu 24:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
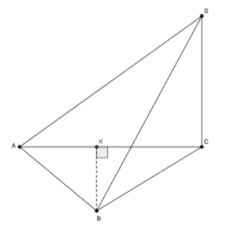
Ta có:
. Do đó câu A và B đúng
C. Sai. vì nếu thì hai mặt phẳng và phải vuông góc với nhau theo giao tuyến SB
D. Ta có:
theo giao tuyến AC
Mà BK là đường cao của .
Vậy D đúng
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
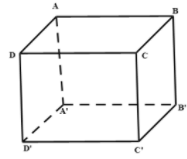
Ta có nên ,
nếu thì vô lý vì H trùng A
Câu 26:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
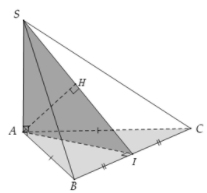
Gọi I là trung điểm của BC
mà
Khi đó H là hình chiếu vuông góc của A lên .
Suy ra .
Câu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
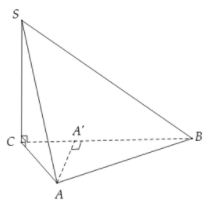
Ta có:
Gọi là hình chiếu vuông góc của A lên ,
khi đó
Suy ra đáp án B sai
Có thể bạn quan tâm
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (544 lượt thi)
- Trắc nghiệm Mặt phẳng vuông góc có đáp án (277 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Nhận biết) (359 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Thông hiểu) (308 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Vận dụng cao) (361 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1262 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (981 lượt thi)
- Trắc nghiệm Khoảng cách (có đáp án) (979 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (801 lượt thi)
- Trắc nghiệm Vectơ trong không gian (có đáp án) (698 lượt thi)
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (675 lượt thi)
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (547 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (525 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (465 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (442 lượt thi)
