Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án)
Trắc nghiệm Toán 11 Ôn tập chương 3 Hình học
-
585 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
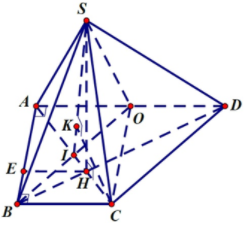
Gọi H=AC∩BD⇒SH⊥(ABCD) và BH=13BD
Kẻ HE⊥AB ⇒AB⊥(SHE) hay
((SAB);(ABCD))=^SEH=60o
Mà HE=13AD=2a3⇒SH=2a√33
Gọi O là trung điểm của AD, ta có ABCD là hình vuông cạnh a
⇒ΔACD có trung tuyến ;
CO=12AD; CD⊥AC
CD⊥(SAC)và BO//CD
hay CD//(SBO) và BO⊥(SAC)
suy ra
d(CD;SB)=d(CD;(SBO))
=d(C;(SBO)).
Tính chất trọng tâm tam giác BCO
⇒IH=13IC=a√26
⇒IS=√IH2+HS2=5a√26
Kẻ CK⊥SI mà CK⊥BO⇒CK⊥(SBO)
⇒d(C;(SBO))=CK
Trong tam giác SIC có
SSIC=12SH.IC=12SI.CK
⇒CK=SH.ICSI=2a√35
Vậy d(CD;SB)=2a√35.
Câu 2:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
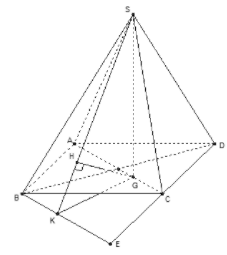
Ta có ABCD là hình bình hành, AB = 2a, BC = a√2, BD =a√6 nên ABCD là hình chữ nhật.
Dựng hình bình hành ACEB.
Ta có AC∥BE, AC ⊄
mà
vậy
.
Dựng lại có nên
Dựng
lại có nên
Ta có .
Tam giác ABC vuông tại B
suy ra
vậy .
Xét tam giác SGK vuông tại G,
đường cao có
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
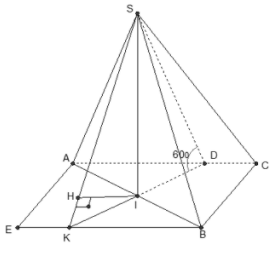
Ta có cùng vuông góc với mặt phẳng nên .
Dựng hình bình hành ACBE.
Ta có
mà vậy
.
Dựng
lại có nên .
Dựng
lại có nên
Kéo dài IK cắt AC tại D mà
Lại có
.
Góc giữa và bằng suy ra .
Ta có
Mà tam giác ABC vuông tại B suy ra
vậy .
Xét tam giác SID vuông tại I,
,suy ra
Xét tam giác SIK vuông tại I, đường cao IH có
Câu 4:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
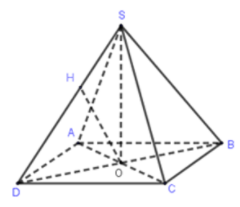
SO⊥(ABCD), O là tâm của hình vuông ABCD.
Kẻ OH⊥SD, khi đó d(O;SD)=OH, α=
OD=
Câu 5:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
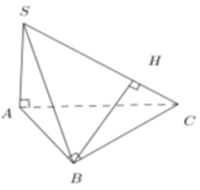
Vì SA, AB, BC vuông góc với nhau từng đôi một nên CB⊥SB
Kẻ BH⊥SC, khi đó d(B;SC)=BH
Ta có: SB=
Trong tam giác vuông SBC ta có:
Câu 6:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
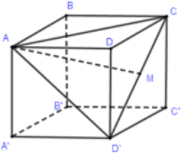
Gọi M là trung điểm của CD′.
Do ABCD.A′B′C′D′ là hình lập phương nên tam giác ACD′ là tam giác đều cạnh
AM⊥CD′⇒d(A,CD′)=AM=
Câu 7:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
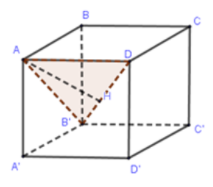
Gọi H là chân đường vuông góc hạ từ A xuống DB′.
Dễ thấy AD⊥(ABB′A′) nên
⇒ΔADB′ vuông đỉnh A.
Lại có AD=a;AB′=
Câu 8:
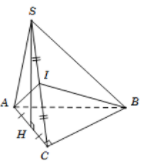
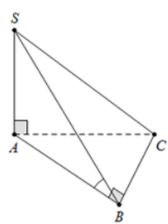
19/07/2024Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I): AI⊥SC
(II): (SBC)⊥(SAC)
(III): AI⊥BC
(IV): (ABI)⊥(SBC)
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Tam giác SAC đều có I là trung điểm của SC nên AI⊥SC.
⇒ Mệnh đề (I) đúng.
Gọi H là trung điểm AC suy ra SH⊥AC.
Mà (SAC)⊥(ABC) theo giao tuyến AC nên SH⊥(ABC) do đó SH⊥BC.
Hơn nữa theo giả thiết tam giác ABC vuông tại C nên BC⊥AC.
Từ đó suy ra BC⊥(SAC)⇒BC⊥AI.. Do đó mệnh đề (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có: ⇒BC⊥(SAC)
BC⊂(SBC)⇒(SBC)⊥(SAC)
Vậy mệnh đề (II) đúng.
Câu 9:
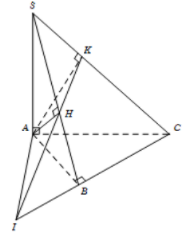
29/09/2024Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Ta có ⇒BC⊥(SAB)
⇒BC⊥AH. Do đó A đúng.
Lại có AH⊥SB. Từ đó suy ra AH⊥(SBC)⇒AH⊥SC. (1)
Lại có theo giả thiết SC⊥AK. (2)
Từ (1) và (2), suy ra
SC⊥(AHK)⇒(SBC)⊥(AHK). Do đó B đúng.
Ta có ⇒SC⊥AI. Do đó C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Câu 10:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
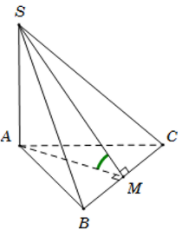
Gọi M là trung điểm của BC, suy ra AM⊥BC
Ta có ⇒BC⊥(SAM)
⇒BC⊥SM
Tam giác ABC đều cạnh a, suy ra trung tuyến AM=
Tam giác vuông SAM có sin
Câu 11:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
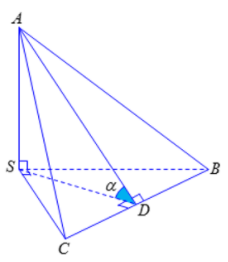
Gọi D là trung điểm cạnh BC.
Ta có ⇒ SA⊥(SBC)
⇒ SA⊥BC.
Mà SD⊥BC nên BC⊥(SAD).
Khi đó tam giác SAD vuông tại S có:
SD= và
Câu 12:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Ta có (SBC)∩(ABC)=BC
Mặt khác SA⊥(ABC) và ΔABC vuông tại B⇒AB⊥BC.
Nên ⇒BC⊥(SAB)⇒BC⊥SB
Xét ΔSAB vuông tại A, có ⇒ SA=AB=a
Mà
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án :
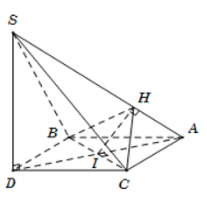
Từ giả thiết suy ra ABDC là hình thoi nên BC⊥AD.
Ta có ⇒BC⊥(SAD)
⇒BC⊥SA.
Lại có theo giả thiết IH⊥SA. Từ đó suy ra SA⊥(HCB)⇒SA⊥BH
⇒ Đáp án A đúng.
Tính được AI=
Ta có ΔAHI∼ΔADS⇒
⇒ Tam giác HBC có trung tuyến IH bằng nửa cạnh đáy BC nên hay BH⊥HC. Do đó D đúng.
Từ mệnh đề A và D suy ra BH⊥(SAC)⇒(SAB)⊥(SAC)⇒ mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Câu 14:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
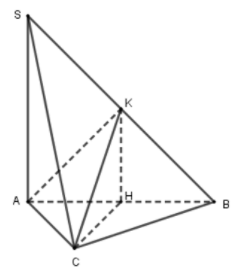
Do ΔABC cân tại C nên CH⊥AB.
Mà SA⊥(ABC) ⇒ SA⊥CH.
Do đó CH⊥(SAB) ⇒ CH⊥HK, CH⊥AK hay A, C đúng.
Ngoài ra HK//SA,SA⊥AB ⇒ HK⊥AB, mà AB⊥CH ⇒AB⊥(CHK) hay B đúng.
D sai vì BC không vuông góc với AC nên không có BC⊥(SAC).
Câu 15:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
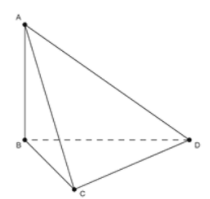
Từ giả thiết ta có ⇒AB⊥(BCD).
Do đó (AC,(BCD)=(AC,BC) =
Câu 16:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
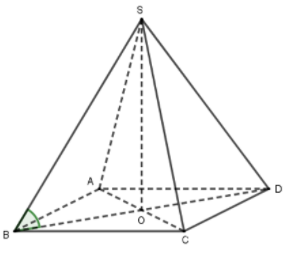
Gọi O là tâm mặt đáy (ABCD), suy ra SO⊥(ABCD).
Vì SO⊥(ABCD), suy ra OA là hình chiếu của SA trên mặt phẳng (ABCD).
Do đó
Tam giác vuông SOA, có tan=
Câu 17:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Phương án A: sai vì chỉ cần giá của chúng song song hoặc nằm trên một mặt phẳng nào đó
Phương án B: sai vì ba véc tơ cùng phương ⇔
Phương án C sai vì điều kiện cần và đủ để ba véc tơ đồng phẳng là có các số m,n sao cho (với không cùng phương).
Câu 18:
23/07/2024Cho ba vectơ không đồng phẳng xét các vectơ
;
Chọn mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Ta thấy nên cùng phương.
Do đó ba véc tơ đồng phẳng.
D sai.
Câu 19:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Có
Câu 20:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
Điểm M thuộc đường thẳng AB nếu và chỉ nếu
Chứng minh:
Ta có: M∈AB⇔
Vậy C đúng.
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
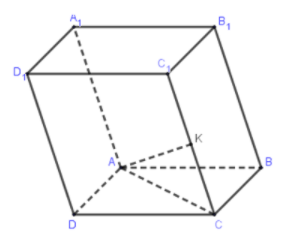
Có
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
Ta có:
Câu 23:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
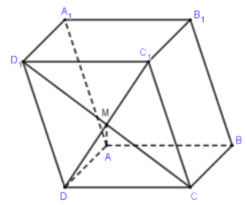
Ta có:
Câu 24:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Ba véc tơ đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nên đáp án A sai.
Câu 25:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Dựa vào đáp án, ta thấy rằng:
+) Với m + n + p = 0 ⇒ m = n = p = 0 suy ra nên chưa kết luận được ba vectơ đồng phẳng.
+) Với m + n + p ≠ 0 suy ra tồn tại ít nhất một số khác 0.
Giả sử m≠0, ta có
Suy ra tồn tại n, p để ba vectơ đồng phẳng.
Câu 26:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Phương án A:
nên A sai
Phương án B nên B sai
Phương án C:
nên C sai.
Phương án D: Do tứ diện ABCD đều nên AB⊥CD hay
Chú ý
Các em có thể dễ dàng chứng minh tứ diện đều ABCD có AB⊥CD bằng cách gọi M là trung điểm của CD và chứng minh CD⊥(ABM), từ đó chứng minh được các cặp cạnh đối còn lại cũng vuông góc.
Câu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
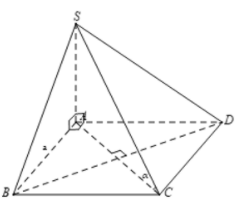
Ta có: SA⊥(ABCD)⇒SA⊥AC
⇒
ABCD là hình vuông cạnh a
⇒ AC=
Câu 28:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
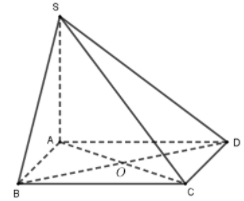
Vì SA vuông góc với mp(ABCD)⇒SA⊥BD.
Mà ABCD là hình thoi tâm O⇒AC⊥BD nên suy ra BD⊥(SAC).
Mặt khác SO⊂(SAC) và SC⊂(SAC)
suy ra
Và AD, SC là hai đường thẳng chéo nhau và .
Ta chưa kết luận được số đo của góc .
Câu 29:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
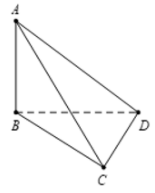
Ta có ⇒AB⊥(BCD)
⇒ tam giác ABD vuông tại B.
Lại có BC⊥CD nên tam giác BCD vuông tại C.
Khi đó:
Câu 30:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
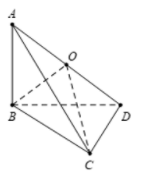
Ta có ⇒AB⊥(BCD)
⇒
Do đó; tam giác ABD vuông tại B.
Suy ra OA=OB=OD=, với O là trung điểm của AD. (1)
Lại có ⇒ CD⊥(ABC)
⇒tam giác ACD vuông tại C.
Suy ra OA=OC=OD= (2)
Từ (1),(2) suy ra OA= OB= OC= OD nên trung điểm O của cạnh AD cách đều A,B,C,D.
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (584 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1378 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (1068 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Khoảng cách (có đáp án) (1070 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (861 lượt thi)
- Trắc nghiệm Vectơ trong không gian (có đáp án) (736 lượt thi)
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (724 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (580 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (573 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (507 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (481 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Thông hiểu) (451 lượt thi)
- Khoảng cách có đáp án (425 lượt thi)
