Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án)
Trắc nghiệm Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
-
760 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
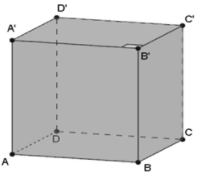
Giả sử xét hình lập phương như hình vẽ có
nhưng
Câu 2:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
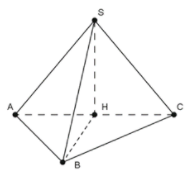
Do nên .
Suy ra H là tâm đường tròn ngoại tiếp .
Mà vuông tại B nên H là trung điểm của AC.
Câu 3:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
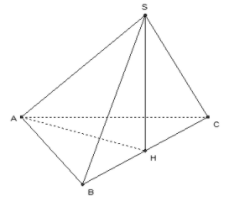
Câu 4:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Vì hình chóp S.ABCD có các cạnh bên bằng nhau
và H là hình chiếu của S lên mặt đáy ABCD
Nên H tâm đường tròn ngoại tiếp tứ giác ABCD
Suy ra .
Nên đáp án B sai.
Câu 5:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
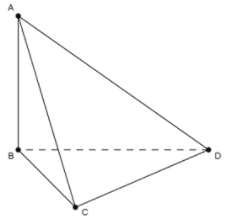
Từ giả thiết ta có
Do đó
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
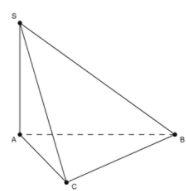
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Do vuông góc với nhau từng đôi một nên , suy ra BC là hình chiếu của AC lên .
Câu 8:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
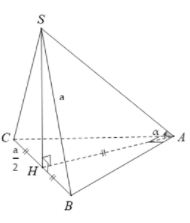
Gọi H là trung điểm của BC suy ra
Ta có:
Câu 9:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
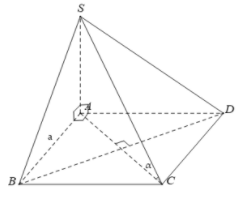
Ta có:
ABCD là hình vuông cạnh a
Câu 10:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
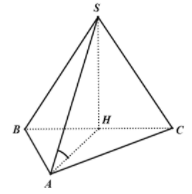
Do H là hình chiếu của S lên mặt phẳng nên
Vậy AH là hình chiếu của SH lên mp
Ta có:
Mà: .
Vậy tam giác SAH vuông cân tại H
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
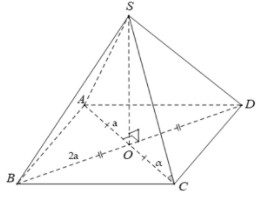
Ta có:
Mặt khác
Suy ra số đo của góc giữa SC và bằng .
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
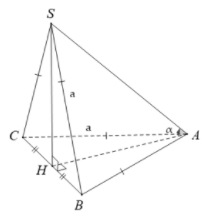
Ta có:
và là hai tam giác đều cạnh a
vuông cân tại H
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
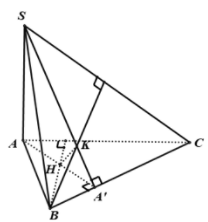
Gọi là đường cao của tam giác ABC
mà
nên
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Gọi lần lượt là hình chiếu của S lên các cạnh
Theo định lý ba đường vuông góc ta có lần lượt là hình chiếu của H lên các cạnh
là tâm dường tròn nội tiếp của
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Hình chóp đều có thể có cạnh bên và cạnh đáy KHÔNG bằng nhau nên đáp án B sai.
Câu 16:
18/07/2024 Xem đáp án
Xem đáp án
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Ta có:
Vậy:
Tương tự :
Từ
Vậy đáp án D đúng.
Câu 18:
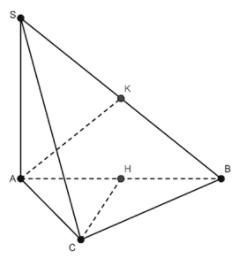
23/07/2024Cho hình chóp S.ABC có cạnh và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Do cân tại C nên .
Suy ra .
Vậy các câu A, B, C đúng nên D sai.
Câu 19:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải::
Câu 20:
21/07/2024Cho hình chóp S.ABC có cạnh và đáy ABC là tam giác cân ở
. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây có thể sai ?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải::
Ta có
Từ đó suy ra
nên A, B, C đúng.
Đáp án D sai trong trường hợp và không bằng nhau Chọn đáp án D.
Câu 21:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
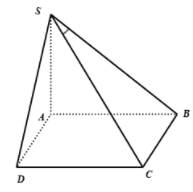
Ta có:
là hình chiếu của S trên
là hình chiếu của C trên
Từ
Xét tam giác SAB vuông tại A ta có:
Xét tam giác SBC vuông tại B ta có:
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
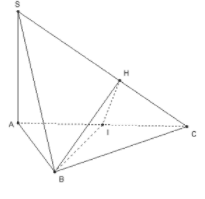
Gọi I là trung điểm của AC, kẻ
Ta có
.
Do đó hay thiết diện là tam giác BIH.
Mà nên hay thiết diện là tam giác vuông.
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
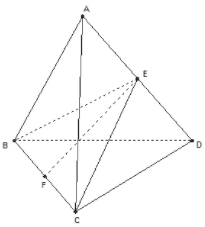
Thiết diện là tam giác BCE, với E là trung điểm của AD.
Gọi F là trung điểm của BC.
Ta có
;
Diện tích thiết diện là:
Câu 24:
18/07/2024Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên Mặt phẳng đi qua trung điểm M của AB và vuông góc với SB cắt lần lượt tại Tứ giác MNPQ là hình gì ?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
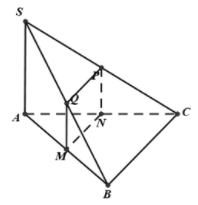
Ta có:
Vậy
Mà
Từ
Tương tự ta có
Mà
Vậy thiết diện là hình thang MNPQ vuông tại N.
Câu 25:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Qua điểm O có thể dựng vô số đường thẳng vuông góc với , các đường thẳng đó cùng nằm trong một mặt phẳng vuông góc với .
Câu 26:
06/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là C
Lời giải:
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song chỉ đúng khi ba đường thẳng đó đồng phẳng.
*Phương pháp giải
Viết giả thiết và kết luận bằng kí hiệu:
|
GT |
a ≠ b, a ⊥ c, b ⊥ c. |
|
KL |
a // b. |
Chứng minh định lí:
Vì a ⊥ c (GT) nên
Vì b ⊥ c (GT) nên
Do đó
Mà hai góc và ở vị trí đồng vị
Suy ra a // b.
Vậy a // b
*Lý thuyết:
Tính chất của hai đường thẳng song song
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
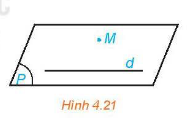
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.
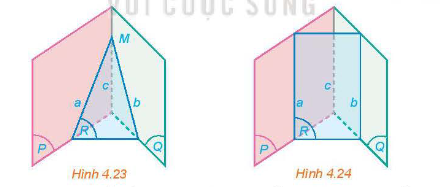
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
XEm thêm
Lý thuyết Hai đường thẳng song song – Toán 11 Kết nối tri thứcCâu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Đường thẳng vuông góc với hai đường thẳng nằm trong thì chỉ đúng khi hai đường thẳng đó cắt nhau.
Câu 28:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
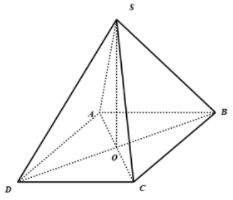
Ta có :
Giả sử (vô lý)
Hay không thể là tam giác vuông
Câu 29:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
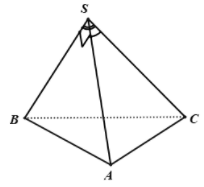
Gọi
Ta có: đều
vuông cân tại S
vuông tại A
Gọi I là trung điểm của AC thì I là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là trục của tam giác ABC thi d đi qua và
Mặt khác : nên .
Vậy nên I là hình chiếu vuông góc của S lên mặt phẳng
Vì H , K lần lượt là trực tâm của tam giác ABC và SBC nên H , K lần lượt thuộc và
Vậy đồng quy tại
Câu 30:
22/07/2024Cho tứ diện OABC có đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng . Xét các mệnh đề sau :
I. Vì nên .
II. Do nên
III. Có và nên
IV. Từ và
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Ta có:
. Vậy I đúng.
. Vậy II đúng.
. Vậy III đúng.
. Vậy IV đúng.
Có thể bạn quan tâm
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (759 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (345 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (446 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Thông hiểu) (385 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Vận dụng) (339 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1183 lượt thi)
- Trắc nghiệm Khoảng cách (có đáp án) (949 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (922 lượt thi)
- Trắc nghiệm Vectơ trong không gian (có đáp án) (670 lượt thi)
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (644 lượt thi)
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (519 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (513 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (498 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (418 lượt thi)
- Khoảng cách có đáp án (374 lượt thi)
