Trắc nghiệm Hai đường thẳng vuông góc (có đáp án)
Trắc nghiệm Toán 11 Bài 2: Hai đường thẳng vuông góc
-
645 lượt thi
-
24 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
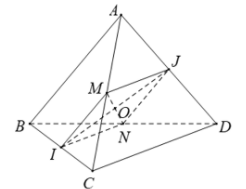
Gọi M, N lần lượt là trung điểm AC, BC.
Ta có:
là hình thoi.
Gọi O là giao điểm của MN và IJ.
Ta có: .
Xét vuông tại O , ta có:
Mà: .
Câu 2:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
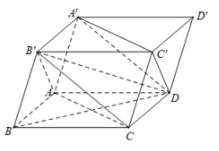
Ta có: (tính chất của hình hộp)
(do giả thiết cho nhọn).
Câu 3:
05/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải
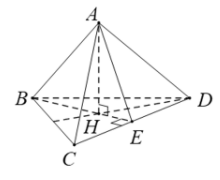
Gọi H là tâm đường tròn ngoại tiếp .
Gọi E là trung điểm CD (do đều).
Do .
Ta có:
*Phương pháp giải
Sử dụng đường thẳng vuông góc với mặt phẳng suy ra 2 đường thẳng vuông góc suy ra góc cần tìm
*Lý thuyến cần nắm về góc giữa hai mặt phẳng:
1. Góc giữa hai đường thẳng là gì?
- Góc giữa hai đường thẳng là góc được tạo bởi hai đường thẳng d và d’ có số đo . Khi d song song hoặc trùng với d’, ta quy ước góc giữa chúng bằng .
- Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương hoặc hai vectơ pháp tuyến của chúng.
2. Cách xác định góc giữa hai đường thẳng
Để xác định góc giữa hai đường thẳng a và b, ta lấy điểm O thuộc 1 trong 2 đương thẳng sau đó vẽ 1 đường thẳng đi qua O và song song với 2 đường còn lại.
Nếu vector u là vector chỉ phương của đường thẳng a, đồng thời vector v là vector chỉ phương của đường thẳng b, góc giữa (u, v) = thì ta có thể suy ra góc giữa 2 đường thẳng a và b bằng ()
- Cho hai đường thẳng d và d’ có vectơ chỉ phương lần lượt là: và . Góc giữa hai đường thẳng được xác định bởi:
- Cho hai đường thẳng d và d’ có vectơ pháp tuyến lần lượt là: và . Góc giữa hai đường thẳng được xác định bởi:
- Gọi k và k’ lần lượt là hệ số góc của hai đường thẳng d và d’. Ta có:
Xem thêm các bài viết liên quan hay, chi tiết:
Công thức tính góc giữa hai đường thẳng (2024) các dạng bài tập và cách giảiCâu 4:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
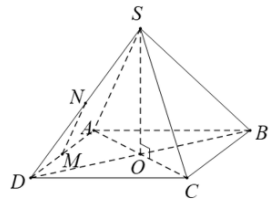
Gọi O là tâm của hình vuông ABCD là tâm đường tròn ngoại tiếp của hình vuông ABCD(1).
Ta có:
nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2)
Từ giả thiết ta có: (do MN là đường trung bình của ).
Xét , ta có:
vuông tại S
.
Câu 5:
22/07/2024Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau.
C sai do:
Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a và b . Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng , nhưng hiển nhiên hai đường thẳng a và b không song song.
D sai do: giả sử a vuông góc với c, b song song với c , khi đó góc giữa a và c bằng , còn góc giữa b và c bằng .
Do đó B đúng.
Câu 7:
25/11/2024 Xem đáp án
Xem đáp án
I. Khối lăng trụ và khối chóp.
- Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
- Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
Ví dụ 1. Ứng với hình lăng trụ tứ giác ABCD.EFGH ta có khối lăng trụ tứ giác ABCD.EFGH; ứng với hình chóp tứ giác S.ABCD ta có khối chóp tứ giác S.ABCD.
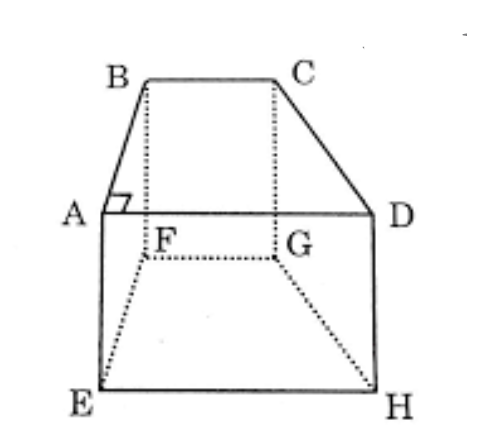
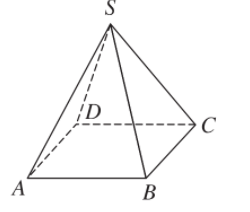
- Ta gọi đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của một hình lăng trụ (hình chóp hay hình chóp cụt) theo thứ tự là đỉnh; cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của khối lăng trụ (khối chóp hay khối chóp cụt) tương ứng.
- Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự.
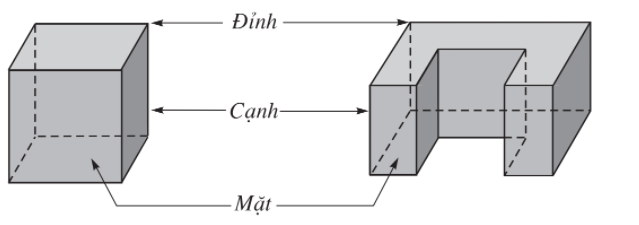
II. Khái niệm về hình đa diện và khối đa diện
1. Khái niệm về hình đa diện
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
- Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là đỉnh, cạnh của hình đa diện.
2. Khái niệm về khối đa diện
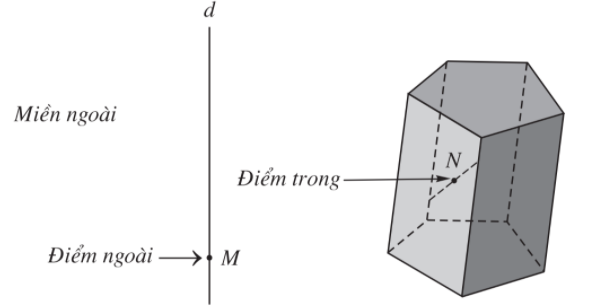
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
Câu 8:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Theo lý thuyết.
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Gọi ,, là 3 đường thẳng cắt nhau từng đôi một. Giả sử , cắt nhau tại A, vì không nằm cùng mặt phẳng với mà cắt , nên phải đi qua A. Thật vậy giả sử không đi qua A thì nó phải cắt tại hai điểm B,C điều này là vô lí, một đường thẳng không thể cắt một mặt phẳng tại hai điểm phân biệt.
Câu 11:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
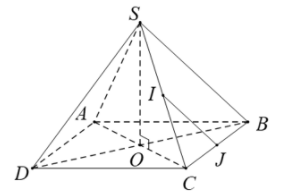
Gọi O là tâm của hình vuông ABCD
là tâm đường tròn ngoại tiếp của hình vuông (1).
Ta có:
nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2)
Từ giả thiết ta có: (do IJ là đường trung bình của ).
.
Mặt khác, ta lại có đều, do đó
Câu 12:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
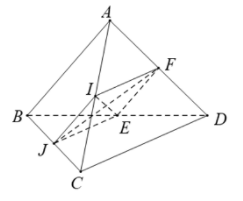
Từ giả thiết ta có: (tính chất đường trung bình trong tam giác)
Từ đó suy ra tứ giác IJEF là hình bình hành.
Mặt khác:
là hình thoi
(tính chất hai đường chéo của hình thoi)
Câu 13:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Câu 14:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Vì và là hình vuông nên
là hình bình hành
Mà là tâm của 2 hình vuông nên là trung điểm của BD và
là đường trung bình của
Mặt khác, nên
Câu 15:
22/07/2024Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu ?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
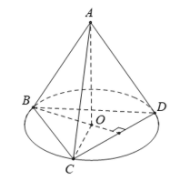
Ta có
Suy ra .
Vậy góc giữa AO và CD là 900.
Câu 16:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
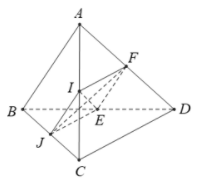
Tứ giác IJEF là hình bình hành.
Mặt khác
mà nên .
Do đó IJEF là hình thoi.
Góc =
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
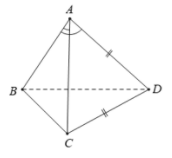
Ta có
Mặt khác
Do có
.
Suy ra .
Câu 18:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Tứ giác là hình bình hành.
Lại có:
Vậy tứ giác là hình chữ nhật.
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
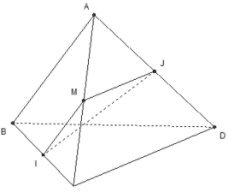
Gọi M là trung điểm của AC.
Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng MI và MJ.
Tính được:
Từ đó suy ra số đo góc giữa hai đường thẳng AB và CD là:
Câu 20:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Do đó:
Câu 22:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
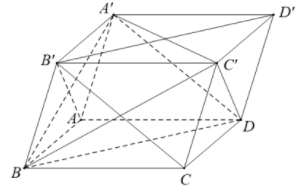
Chú ý: Hình hộp có tất cả các cạnh bằng nhau còn gọi là hình hộp thoi.
A đúng vì:
B sai vì:
C đúng vì:
.
D đúng vì:
.
Câu 23:
23/07/2024Cho tứ diện ABCD. Chứng minh rằng nếu thì , , . Điều ngược lại đúng không?
Sau đây là lời giải:
Bước 1:
Bước 2: Chứng minh tương tự, từ
ta được và ta được .
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
 Xem đáp án
Xem đáp án
Câu 24:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
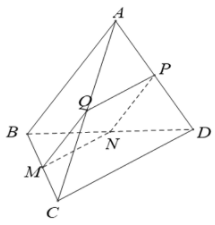
Ta có:
Tương tự ta có:
.
Do đó tứ giác MNPQ là hình bình hành
lại có .
Vậy tứ giác MNPQ là hình chữ nhật.
Có thể bạn quan tâm
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (644 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1183 lượt thi)
- Trắc nghiệm Khoảng cách (có đáp án) (949 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (922 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (760 lượt thi)
- Trắc nghiệm Vectơ trong không gian (có đáp án) (670 lượt thi)
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (519 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (513 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (498 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (446 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (418 lượt thi)
