Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Trong các mệnh đề sau mệnh đề nào đúng?

Đáp án đúng là: A

Lời giải

Tứ diện ABCD có hai cặp cạnh đối vuông góc tứ diện có ít nhất một mặt là tam giác nhọn.

*Phương pháp giải:

Nắm chắc lý thuyết tứ diện

*Lý thuyết:

I. Khối lăng trụ và khối chóp.

- Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.

Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.

- Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.

- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.

Ví dụ 1. Ứng với hình lăng trụ tứ giác ABCD.EFGH ta có khối lăng trụ tứ giác ABCD.EFGH; ứng với hình chóp tứ giác S.ABCD ta có khối chóp tứ giác S.ABCD.

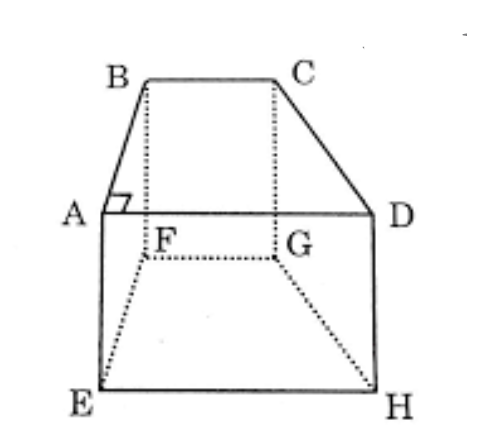
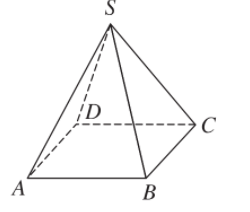
- Ta gọi đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của một hình lăng trụ (hình chóp hay hình chóp cụt) theo thứ tự là đỉnh; cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của khối lăng trụ (khối chóp hay khối chóp cụt) tương ứng.

- Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự.

II. Khái niệm về hình đa diện và khối đa diện

1. Khái niệm về hình đa diện

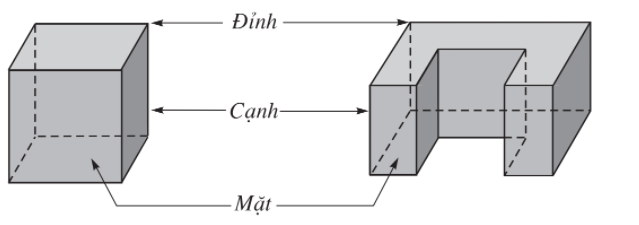
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:

a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.

b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

- Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là đỉnh, cạnh của hình đa diện.

2. Khái niệm về khối đa diện

- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.

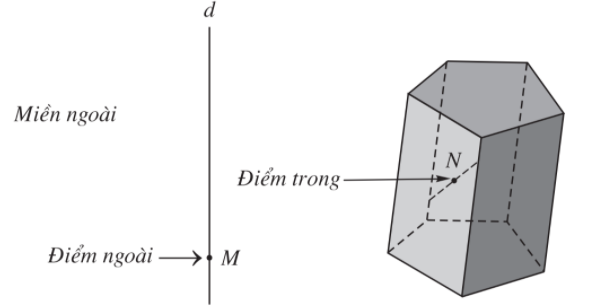
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.

Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.

- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.

Xem thêm

TOP 40 câu Trắc nghiệm Hai đường thẳng vuông góc (có đáp án ) – Toán 11 

Lý thuyết Khái niệm về khối đa diện (mới 2024 + Bài Tập) – Toán 12