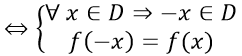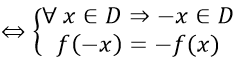(3cosx – 2)(2cosx + 3m – 1) = 0 (*)

Đặt t = cosx (−1 ≤ t ≤ 1).

Nếu t = −1 thì tồn tại 1 giá trị x = π.

Nếu $t\in (-1;0)$  thì tồn tại 2 giá trị $x\in \left(0;\frac{3\pi }{2}\right)\backslash \text{{}\pi \text{}}$ .

Nếu $t\in \text{[}0;1)$  thì tồn tại 1 giá trị $x\in \left(0;\frac{\pi }{2}\right]$ .

Phương trình (*) trở thành:

$(3t-2)(2t+3m-1)=0\iff \left[\begin{array}{l}3t-2=0\left(1\right)\\ 2t+3m-1=0\left(2\right)\end{array}\right.$

Phương trình (1) có 1 nghiệm t = $\frac{2}{3}$  thuộc nửa khoảng [0; 1)

Nên phương trình (*) có 1 nghiệm $x\in \left(0;\frac{\pi }{2}\right]$ .

Do đó phương trình (*) có 3 nghiệm phân biệt $x\in \left(0;\frac{3\pi }{2}\right)$  khi và chỉ khi phương trình (2) phải có 1 nghiệm $t\in (-1;0)$ .

Do đó, ta có:

$-1<\frac{1-3m}{2}<0\iff -2<1-3m<0$

$\iff -3<-3m<-1\iff \frac{1}{3}<m<1$

Vậy không có giá trị nguyên của m thỏa mãn yêu cầu đề bài.

Chọn đáp án D

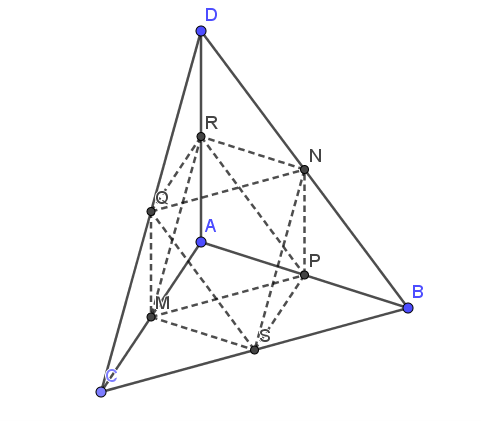
Theo hình vẽ, dễ thấy M, P, R, S không đồng phẳng.

Chọn đáp án C

Điểm S cùng với hai trong số bốn điểm A, B, C, D tạo thành một mặt phẳng.

Từ bốn điểm ta có 6 cách chọn ra hai điểm, nên có tất cả 6 mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên.

Chọn đáp án A

Để phương trình 5sinx – 12cosx = m có nghiệm thì:

$5^2+{12}^2\ge m^2\iff m^2\le 169$

$\iff -13\le m\le 13$

Vậy có 27 giá trị nguyên m thỏa mãn yêu cầu đề bài.

Chọn đáp án D.

Xét phương trình sinx + 3 = 0 

$\iff$ sinx = −3.

Mà −1 ≤ sinx ≤ 1.

Do đó, phương trình vô nghiệm.

Chọn đáp án B

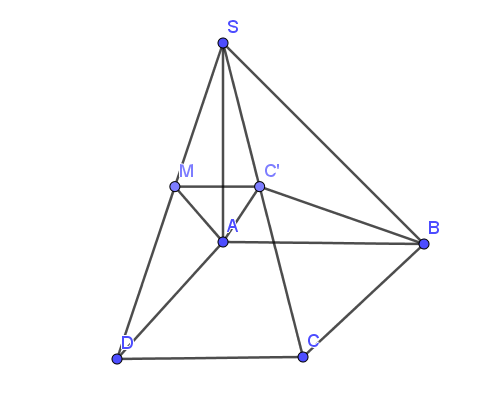
Từ hình vẽ, ta có thiết diện của hình chóp với mặt phẳng (ABC’) là đa giác MC’BA có 4 cạnh.

Chọn đáp án C

Điều kiện xác định của hàm số $y=\frac{1-\sin x}{\cos x}$  là:

$\cos x\ne 0$

$\iff \cos x\ne cos\frac{\pi }{2}$

$\iff x\ne \pm \frac{\pi }{2}+k2\pi$, $k\in \mathbb{Z}$

$\iff x\ne \frac{\pi }{2}+k\pi$,$k\in \mathbb{Z}$

Chọn đáp án B

Gọi d’ là ảnh của d qua phép đối xứng tâm I

Lấy điểm M(x; y) thuộc d tùy ý, ta có: x + 2y + 3  = 0

Gọi M’(x’; y’) là ảnh của M(x; y) qua phép đối xứng tâm I

Do đó, ta có:$\overrightarrow{IM\text{'}}=-\overrightarrow{IM}$ .

Khi đó,

$\left\{\begin{array}{l}x\text{'}-1=-x+1\\ y\text{'}-1=-y+1\end{array}\right.\iff \left\{\begin{array}{l}x=2-x\text{'}\\ y=2-y\text{'}\end{array}\right.$

Mà M thuộc đường thẳng d nên ta có:

x + 2y + 3 = 0

$\iff$ (2 – x’) + 2(2 – y’) + 3 = 0

$\iff$ -x’ – 2y’ + 9 = 0

$\iff$ x’ + 2y’ – 9 = 0.

Vậy phương trình đường thẳng d’ là: x + 2y – 9 = 0.

Chọn đáp án D.

Ta có: $A_n^k=\frac{n!}{(n-k)!}=\frac{n!}{k!(n-k)!}.k!=C_n^k.k!$

Do đó, khẳng định (A) là sai.

Chọn đáp án A

Gọi số tự nhiên thỏa mãn yêu cầu đề bài là: $\overline{abc}$ .

Số cách chọn chữ số a là 5 cách (trừ chữ số 0).

Số cách chọn chữ số b là 5 cách (khác a).

Số cách chọn chữ số c là 4 cách (khác a, b).

Số số tự nhiên thỏa mãn yêu cầu đề bài là: 5.5.4 = 100.

Chọn đáp án A

Hàm số y = sinx đồng biến trên khoảng $\left(-\frac{\pi }{2};0\right)$ .

Do đó, nó đồng biến trên khoảng $\left(-\frac{\pi }{4};-\frac{\pi }{6}\right)$ .

Chọn đáp án D

Giả sử điểm A(x₀; y₀) thì điểm đối xứng với điểm A qua trục tung là điểm A’(-x₀; y₀).

Gọi M’(x; y) là điểm đối xứng với M qua trục tung.

Do đó, ta có: $\left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$  

$\Rightarrow$ M’(-3; -4).

Chọn đáp án B

Số vectơ khác khác vectơ-không, có điểm đầu và điểm cuối là các điểm đã cho là chỉnh hợp chập 2 của 12 phần tử: $A_{12}^2=132$  (vectơ).

Chọn đáp án B

Ta có $AB=\sqrt{{(-3-1)}^2+{(2-5)}^2}=5$.

Do A, B theo thứ tự là ảnh của các điểm M, N qua phép vị tự tâm O tỉ số k = -2 nên ta có: AB = |-2| MN $\Rightarrow MN=\frac{AB}{2}=\frac{5}{2}$.

Chọn đáp án D

Vị trí nhất có thể có 8 kết quả xảy ra.

Vị trí nhì có thể có 7 kết quả xảy ra.

Vị trí ba có thể có 6 kết quả xảy ra.

Vậy số kết quả xảy ra đối với các vị trí nhất, nhì, ba là: 8.7.6 = 336.

Chọn đáp án C

Gọi M’(x; y) là ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{v}$ .

Có:$\overrightarrow{MM\text{'}}$ = (x – 3; y – 2).

Mà $\overrightarrow{MM\text{'}}$ = $\overrightarrow{v}$ .

Khi đó,$\left\{\begin{array}{l}x-3=2\\ y-2=1\end{array}\right.\iff \left\{\begin{array}{l}x=5\\ y=3\end{array}\right.$

Vậy điểm M’ có tọa độ là: M’(5; 3).

Chọn đáp án B

Số cách cử 1 bạn làm Bí thư là 7 cách.

Số cách cử 1 bạn làm Phó bí thư là 6 cách.

Số cách cử 1 bạn làm Ủy viên là 5 cách.

Vậy số cách cử 3 bạn trong 7 bạn này giữ các vị trí Bí thư, Phó Bí thư, Ủy viên, biết mỗi bạn chỉ đảm nhận 1 nhiệm vụ là: 7.6.5 = 210 (cách).

Chọn đáp án D

Ta có: $C_n^2-n=135$

$\iff \frac{n!}{2!(n-2)!}-n=135$

$\iff \frac{n(n-1)(n-2)!}{2(n-2)!}-n=135$

$\iff \frac{n(n-1)}{2}-n=135$

$\iff \frac{n(n-1)}{2}-\frac{2n}{2}=\frac{270}{2}$

$\iff n^2-n-2n=270$

$\iff n^2-3n-270=0$

$\iff \left[\begin{array}{l}n=18\\ n=-15\end{array}\right.$

Mà n luôn dương, do đó chọn n = 18.

Chọn đáp án B

Ta có: $-1\le \sin x\le 1$

$\iff 2\le \sin x+3\le 4$

$\iff \sqrt{2}\le \sqrt{\sin x+3}\le 2$

$\iff 4\sqrt{2}\le 4\sqrt{\sin x+3}\le 8$

$\iff 4\sqrt{2}-1\le 4\sqrt{\sin x+3}-1\le 7$

Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=4\sqrt{\sin x+3}-1$ lần lượt là:

$4\sqrt{2}-1$ và 7.

Chọn đáp án B

Xét phương trình $\tan x+\tan \left(x+\frac{\pi }{4}\right)=1$(*)

Điều kiện xác định của phương trình là:  

$\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+k\pi \\ x\ne \frac{\pi }{4}+k2\pi \\ x\ne \frac{-3}{4}\pi +k2\pi \end{array}\right.$với $k\in \mathbb{Z}$

Khi đó, phương trình (*) trở thành:

$\frac{\sin x}{\cos x}+\frac{\sin \left(x+\frac{\pi }{4}\right)}{cos\left(x+\frac{\pi }{4}\right)}=1$

$\iff \frac{\sin x}{\cos x}+\frac{\sin x+\cos x}{\cos x-\sin x}=1$

$\Rightarrow \sin x(\cos x-\sin x)+\cos x(\sin x+\cos x)=\cos x(\cos x-\sin x)$

$\iff \sin x.\cos x-{\sin }^{2}x+\sin x.\cos x+co{s}^{2}x=co{s}^{2}x-\cos x.\sin x$

$\iff 2\sin x\cos x+co{s}^{2}x-{\sin }^{2}x=co{s}^{2}x-\sin x\cos x$

$\iff 3\sin x\cos x-{\sin }^{2}x=0$

$\iff \sin x\left(3\cos x-\sin x\right)=0$

$\iff \left[\begin{array}{l}\sin x=0\\ 3\cos x-\sin x=0\end{array}\right.$

+) Ta có: sinx = 0

$\iff \sin x=\sin 0$

$\iff \left[\begin{array}{l}x=k2\pi \\ x=\pi +k2\pi \end{array}\right.$

$\iff x=k\pi$, $k\in \mathbb{Z}$  (TMĐK)

Kết hợp với điều kiện ở đầu bài và chọn 2 điểm có nghiệm trên đường tròn lượng giác lần lượt biểu diễn bởi điểm A và B.

+) Giải phương trình 3cosx – sinx = 0 ta có:

3cosx – sinx = 0

$\iff 3\cos x=\sin x$

$\iff \frac{\sin x}{\cos x}=3$

$\iff \tan x=3$

x = α + kπ, với α = acrtan 3 + kπ ( $k\in \mathbb{Z}$).

Kết hợp với điều kiện ở đầu bài và chọn hai nghiệm biểu diễn lần lượt bởi điểm C và D.

Ta cần tính diện tích hình chữ nhật ABCD.

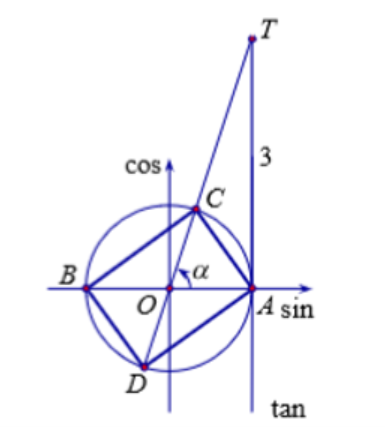
Xét tam giác vuông AOT có:

$OT=\sqrt{O{A}^2+A{T}^2}=\sqrt{10}$ (theo định lý Py-ta-go)

$\Rightarrow \sin \alpha =\frac{AT}{OT}=\frac{3}{\sqrt{10}}$ (1)

Xét tam giác ACD có:

$\widehat{ADC}=\frac{\alpha }{2}\Rightarrow \sin \frac{\alpha }{2}=\frac{AC}{2}$ và $cos\frac{\alpha }{2}=\frac{AD}{2}$

Từ đó ta có:

$2\sin \frac{\alpha }{2}.cos\frac{\alpha }{2}=\frac{3}{\sqrt{10}}$

$\Rightarrow 2.\frac{AC}{2}.\frac{AD}{2}=\frac{\sqrt{3}}{10}$

$\Rightarrow AC.AD=\frac{6}{\sqrt{10}}$

Vậy diện tích tứ giác ACBD là: $AC.AD=\frac{6}{\sqrt{10}}=\frac{3\sqrt{10}}{5}$  (đvdt).

Chọn đáp án A

Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử khác nhau là tổ hợp chập 3 của 7 phần tử: $C_7^3$.

Chọn đáp án C

Hàm y = tanx có chu kì tuần hoàn là π.

Hàm y = tan$\left(\frac{x}{2}\right)$  có chu kỳ tuần hoàn là: $\frac{\pi }{\frac{1}{2}}=2\pi$.

Chọn đáp án A

Số cách bạn An lấy 3 bông hoa từ giỏ không kể màu sắc là: $C_{11}^3$  (cách).

Số cách bạn An lấy 3 bông hoa từ giỏ chỉ có màu vàng là: $C_6^3$  (cách).

Số cách bạn An lấy 3 bông hoa từ giỏ chỉ có màu đỏ là: $C_5^3$  (cách).

Số cách bạn An lấy 3 bông hoa từ giỏ đó sao cho chúng có đủ cả hai màu là:

$C_{11}^3$ - $C_6^3$  - $C_5^3$ = 135 (cách).

Chọn đáp án C

Gọi M’(x’; y’) là ảnh của điểm M(2; 2) qua phép quay tâm O góc quay 45$°$

Ta có: 

$\left\{\begin{array}{l}x\text{'}=2cos{45}^o-2\sin {45}^o=0\\ y\text{'}=2cos{45}^o+2\sin {45}^o=2\sqrt{2}\end{array}\right.$

$\Rightarrow$M’(0; 2$\sqrt{2}$).

Chọn đáp án C

Số cách xếp 6  người vào 6 ghế là 6!

Ta tính số cách xếp sao cho A và F ngồi cạnh nhau:

Xem AF là một phần tử X, ta có 5! = 120  cách xếp 5 người X; B; C; D; E.

Khi hoán vị A và F ta có thêm được một cách xếp.

Vậy có 2.120 = 240 cách xếp để A và F ngồi cạnh nhau.

Do đó, số cách xếp để A  và F không ngồi cạnh nhau là: 6! – 240 = 480 cách.

Chọn đáp án A

Đáp án đúng là A

*Phương pháp giải

Sử dụng định nghĩa

Hàm số y = f(x) xác định trên D

    + Hàm số chẵn 

    + Hàm số lẻ 

Chú ý: Một hàm số có thể không chẵn cũng không lẻ

        Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng

        Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng

* Quy trình xét hàm số chẵn, lẻ.

B1: Tìm tập xác định của hàm số.

B2: Kiểm tra

    Nếu ∀ x ∈ D ⇒ -x ∈ D Chuyển qua bước ba

    Nếu ∃ x₀ ∈ D ⇒ -x₀ ∉ D kết luận hàm không chẵn cũng không lẻ.

B3: xác định f(-x) và so sánh với f(x).

    Nếu bằng nhau thì kết luận hàm số là chẵn

    Nếu đối nhau thì kết luận hàm số là lẻ

    Nếu tồn tại một giá trị ∃ x₀ ∈ D mà f(-x₀ ) ≠ ± f(x₀) kết luận hàm số không chẵn cũng không lẻ.

*Lời giải

Xét hàm số: f(x) = $y=\frac{\cos x}{1+x^2}$ .

Ta có: f(-x) =$\frac{\cos (-x)}{1+{(-x)}^2}=\frac{\cos x}{1+x^2}$.

Do đó, f(x) = f(-x).

Vậy hàm số $y=\frac{\cos x}{1+x^2}$ là hàm số chẵn.

Hơn nữa $1+x^2>0\forall x\in ℝ$ nên hàm số $y=\frac{\cos x}{1+x^2}$ là hàm số chẵn trên $ℝ$.

$\to$Chọn A

Xem thêm các bài viết liên quan hay, chi tiết:

Phương pháp xét tính chẵn, lẻ của hàm số chi tiết nhất

Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác và cách giải

Số cách chọn ra 3 bạn để tham gia vào đội xung kích là tổ hợp chập 3 của 45 phần tử: $C_{45}^3$.

Chọn đáp án C

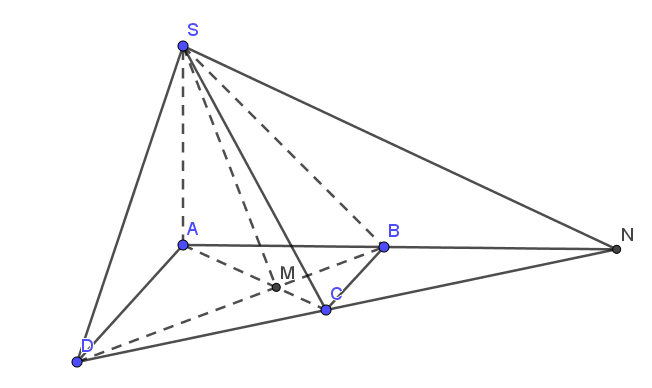
Theo hình vẽ ta có:

SM nằm trong mặt phẳng (SAC).

SM nằm trong mặt phẳng (SBD).

Do đó, SM là giao tuyến của mặt phẳng (SAC) và (SBD).

Chọn đáp án A

Ta có: tan2x – 1 = 0 (*)

Điều kiện xác định: cos 2x ≠ 0 $\iff 2x\ne k\pi \iff x\ne k\frac{\pi }{2},k\in \mathbb{Z}$

$\iff \tan 2x=1$

$\iff \tan 2x=\tan \frac{\pi }{4}$

$\iff 2x=\frac{\pi }{4}+k\pi$, $k\in \mathbb{Z}$

$\iff x=\frac{\pi }{8}+k\frac{\pi }{2}$, $k\in \mathbb{Z}$

Kết hợp với điều kiện $x\ne k\frac{\pi }{2},k\in \mathbb{Z}$ .

Vậy nghiệm của phương trình (*) là: $x=\frac{\pi }{8}+k\frac{\pi }{2},k\in \mathbb{Z}$ .

Chọn đáp án B

Xét đường tròn (C): ${(x-1)}^2+{(y-1)}^2=4$  có tâm I(1; 1) và bán kính R = 2.

Vì (C’) là ảnh của (C) qua phép vị tự tâm I(1; 1) tỉ số k với k > 0.

Nên ta có: I’(x; y) và R’ = 2k.

Ta có: $\overrightarrow{II\text{'}}=\overrightarrow{II}=\overrightarrow{0}\Rightarrow \left\{\begin{array}{l}x-1=0\\ y-1=0\end{array}\right.\iff \left\{\begin{array}{l}x=1\\ y=1\end{array}\right.\Rightarrow I\text{'}(1;1)$

Vậy phương trình đường tròn (C’) có dạng: ${(x-1)}^2+{(y-1)}^2={\left(2k\right)}^2$.

Mà đường tròn (C’) đi qua điểm M(5; 4) nên ta có:

(5 – 1)² + (4 – 1)² = (2k)²

$\iff$ 4² + 3² = (2k)²

$\iff$(2k)² = 25

$\iff$(2k)² = 5²

 $\iff$2k = 5

$\iff k=\frac{5}{2}$.

Chọn đáp án B

a) $y=\frac{1+\tan x}{\sin x}$

Điều kiện xác định của hàm số là:

$\left\{\begin{array}{l}\cos x\ne 0\\ \sin x\ne 0\end{array}\right.\iff \left\{\begin{array}{l}\cos x\ne cos\frac{\pi }{2}\\ \sin x\ne \sin 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+k2\pi \\ x\ne -\frac{\pi }{2}+k2\pi \\ x\ne k2\pi \\ x\ne \pi +k2\pi \end{array}\right.$

$\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+k\pi \\ x\ne k\pi \end{array}\right.\iff x\ne k\frac{\pi }{2}$, với $k\in \mathbb{Z}$

Vậy tập xác định của hàm số là:$D=ℝ\backslash \left\{k\frac{\pi }{2}|k\in \mathbb{Z}\right\}$.

b) ${\sin }^{2}x-\sin 2x=0$  (*)

$\iff {\sin }^{2}x-2\sin x\cos x=0$

$\iff \sin x(\sin x-2\cos x)=0$

$\iff \left[\begin{array}{l}\sin x=0\\ \sin x-2\cos x=0\end{array}\right.$

$\iff \left[\begin{array}{l}\sin x=0\\ \sin x=2\cos x\end{array}\right.$

+) Ta có: sinx = 0

$\iff \sin x=\sin 0$

$\iff \left[\begin{array}{l}x=k\pi \\ x=\pi +k\pi \end{array}\right.$, $k\in \mathbb{Z}$

$\iff x=k\pi$ , $k\in \mathbb{Z}$

+) Ta có: sinx = 2cosx

Với cosx = 0 thì sinx = 1 (vì sin²x + cos²x = 1)

Khi đó 1 = 0 (vô lý)

Với cosx ≠ 0 thì: $\frac{\sin x}{\cos x}=2$

$\iff \tan x=2$

$\Rightarrow x=arc\tan 2+k\pi$ , $k\in \mathbb{Z}$

Với họ nghiệm trên, cosx ≠ 0, do đó họ nghiệm x = arctan 2 + kπ, $k\in \mathbb{Z}$  thỏa mãn.

Vậy tập nghiệm của phương trình (*) là:$\left\{k\pi ;arc\tan 2+k\pi |k\in \mathbb{Z}\right\}$ .

Gọi M(x; y) là điểm thuộc đường thẳng d, M’(x’; y’) là ảnh của M qua phép vị tự tâm I tỉ số k = 2.

Do đó, ta có:

$\overrightarrow{IM}$ = (x – 1; y – 2)

 $\overrightarrow{IM\text{'}}$ = (x’ – 1; y’ – 2)

Mà $\overrightarrow{IM\text{'}}$  = 2$\overrightarrow{IM}$ .

Khi đó,

$\left\{\begin{array}{l}x\text{'}-1=2(x-1)\\ y\text{'}-2=2(y-2)\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}-1=2x-2\\ y\text{'}-2=2y-4\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{x\text{'}+1}{2}\\ y=\frac{y\text{'}+2}{2}\end{array}\right.$

Mà M(x; y) là điểm thuộc đường thẳng d nên ta có:

$\frac{x\text{'}+1}{2}+2.\frac{y\text{'}+2}{2}+3=0$

$\Rightarrow$ x’ + 1 + 2y’ + 4 + 6 = 0

$\Rightarrow$ x’ + 2y’ + 11 = 0

Mà đường thẳng d’ là ảnh của đường thẳng d qua phép vị tự tâm I(1; 2) tỉ số k = 2.

Nên M’ thuộc d’ nên phương trình đường thẳng d’ là: x + 2y + 11 = 0.

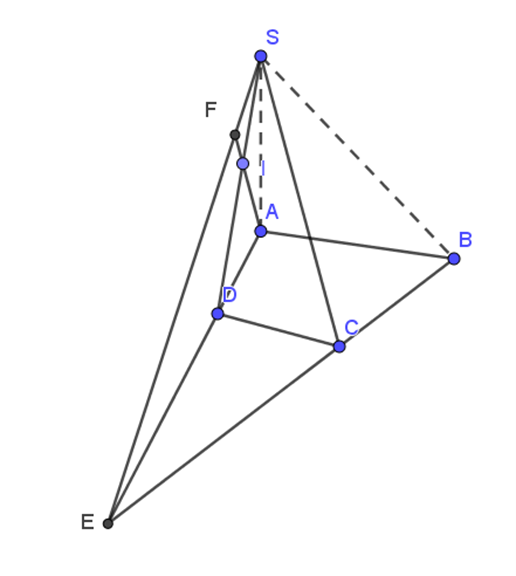
Kẻ BC giao AD tại E, nối E với S ta được SE.

Do S và E nằm trong mặt phẳng (SAD) nên SE nằm trong mặt phẳng (SAD).

Do S và E nằm trong mặt phẳng (SBC) nên SE nằm trong mặt phẳng (SBC).

Do đó, SE là giao tuyến của mặt phẳng (SAD) và mặt phẳng (SBC).

Mặt khác, AI nằm trong mặt phẳng (SAD).

Kẻ AI cắt SE tại F.

Khi đó, F thuộc SE nên F thuộc mặt phẳng (SBC) mà A, I, F thẳng hàng.

Do đó, F chính là giao điểm của AI với mặt phẳng (SBC).