Đáp án đúng là: A

Gọi (x; y) là tọa độ của ảnh của M(–3; 4) qua phép quay tâm O, góc quay 90°

Ta có: $\left\{\begin{array}{l}x=-4\\ y=-3\end{array}\right.$

Vậy ảnh của M(–3; 4) qua phép quay tâm O, góc quay 90° là N(–4; –3). 

Đáp án đúng là: D

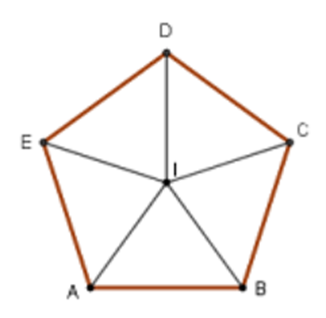
Vì ABCDE là ngũ giác đều tâm I nên IA = IB = IC = ID = IE và $\widehat{CID}=\widehat{DIE}=\widehat{EIA}=\widehat{AIB}=\widehat{BIC}=72°$

Từ đó, ta có: 

$Q_{(I\mathrm{,144}°)}\left(B\right)=A$

$Q_{(I\mathrm{,144}°)}\left(C\right)=B$

Do đó, $Q_{(I\mathrm{,144}°)}\left(BC\right)=AB$

Đáp án đúng là: D

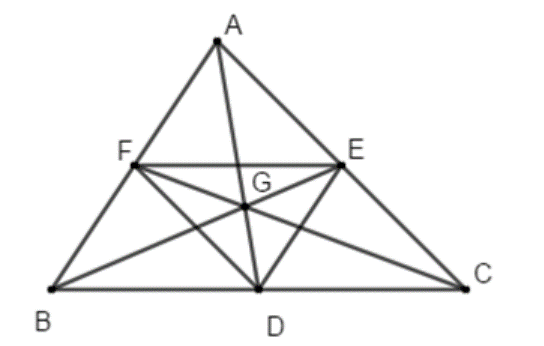
Do G là trọng tâm của tam giác ABC nên ta có: $AG=\frac{2}{3}AD;GD=\frac{1}{3}AD$

$\Rightarrow GD=\frac{1}{2}AD$

$\Rightarrow 2\overrightarrow{DG}=\overrightarrow{GA}$

Vậy  $T_{2\overrightarrow{DG}}\left(G\right)=A$

Đáp án đúng là: C

Xếp các chữ số 0, 1, 2, 3, 5 thành một hàng ngang có 4 vị trí có số cách là: $A_5^4$

Xếp các chữ số 0, 1, 2, 3, 5 thành một hàng ngang có 4 vị trí trong đó chữ số 0 đứng đầu có số cách là: $A_4^3$

Số các số tự nhiên gồm 4 chữ số đôi một khác nhau lập từ các chữ số 0, 1, 2, 3, 5 là: $A_5^4$  – $A_4^3$  = 96 (số)

Gọi số tự nhiên gồm 4 chữ số đôi một khác nhau lập từ các chữ số 0, 1, 2, 3, 5 chia hết cho 5 có dạng  $\overline{abcd}$

TH1: d = 0

Số các số tự nhiên thỏa mãn là:$A_4^3$ = 24

TH2: d = 5

Chữ số a có 3 cách chọn

Chữ số b có 3 cách chọn

Chữ số c có 2 cách chọn

Số các số tự nhiên thỏa mãn là: 3.3.2 = 18

Số số tự nhiên không chia hết cho 5 gồm 4 chữ số khác nhau là: 96 – 24 – 18 = 54 (số).

Đáp án đúng là: C

Muốn có một tứ giác, ta cần chọn 2 điểm thuộc đường thẳng a và 2 điểm trên đường thẳng b

Số cách chọn 2 điểm thuộc đường thẳng a là: $C_m^2$

Số cách chọn 2 điểm thuộc đường thẳng b là: $C_n^2$

Vậy số tứ giác có 4 định thuộc tập hợp các điểm đã cho là: $C_m^2$ . $C_n^2$

Đáp án đúng là: C

Lời giải

Điều kiện xác định của hàm số $y=\frac{1}{\sin 2x+1}$ là:

$\sin 2x+1\ne 0$

$\iff \sin 2x\ne -1$

$\iff \sin 2x\ne \sin \frac{-\pi }{2}$

$\iff \left\{\begin{array}{l}2x\ne \frac{-\pi }{2}+k2\pi \\ 2x\ne \frac{3\pi }{2}+k2\pi \end{array}\right.$ với $k\in \mathbb{Z}$

$\iff \left\{\begin{array}{l}x\ne \frac{-\pi }{4}+k\pi \\ x\ne \frac{3\pi }{4}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

$\iff \left\{\begin{array}{l}x\ne \frac{-\pi }{4}+k\pi \\ x\ne \frac{3\pi }{4}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

Vậy tập xác định của hàm số $y=\frac{1}{\sin 2x+1}$  là $D=ℝ\backslash \left\{-\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\right\}$ .

*Phương pháp giải:

Hàm phân thức xác định khi và chỉ khi mẫu khác 0

*Lý thuyết:

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

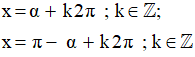
Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}\frac{-\pi }{2}\le \alpha \le \frac{\pi }{2}\\ \sin \alpha =a\end{array}\right.$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

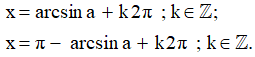
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi$ và $x=\pi -\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$

Tổng quát: 

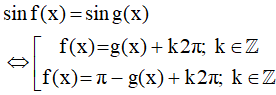
b) Phương trình sinx = sinβ⁰ có các nghiệm là:

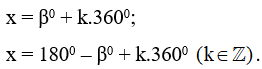
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x=-\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = 0:  Phương trình sinx = 0 có các nghiệm là $x=k\pi ;k\in \mathbb{Z}$.

2. Phương trình cosx = a.

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $\left|\text{cosx }\right|\le 1$ với mọi x.

- Trường hợp $\left|\text{\hspace{0.17em}a }\right|\le 1$.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x=\pm \alpha +k2\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: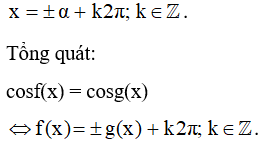 

b) Phương trình cos x= cosβ⁰ có các nghiệm là $x=\pm {\beta }^0+\text{\hspace{0.17em}}k{360}^0;k\in \mathbb{Z}$

c) Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}0\le \alpha \le \pi \\ \cos \alpha =a\end{array}\right.$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

$x=\pm \arccos a\text{\hspace{0.17em}}+k2\pi ;k\in \mathbb{Z}$

d) Các trường hợp đặc biệt:

+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: $x=k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là: $x=\pi +k2\pi ;k\in \mathbb{Z}$

+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới  + Bài Tập) – Toán 11 

Đáp án đúng là: D

Xét hàm số $y=2019\cos x+2020$ ta có:

$f\left(x\right)=2019\cos x+2020$

$f(-x)=2019\cos (-x)+2020=2019\cos x+2020$ (vì cos(–x) = cosx)

Do đó, ta có: f(x) = f(–x) nên hàm số $y=2019\cos x+2020$ là hàm số chẵn

Đáp án đúng là: B.

Ta có:  $C_n^k=C_{n-1}^{k-1}+C_{n-1}^k$

Đáp án đúng là: B

$\sin x+\sqrt{3}\cos x=1$

$\iff \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x=\frac{1}{2}$

$\iff cos\frac{\pi }{3}\sin x+\sin \frac{\pi }{3}\cos x=\frac{1}{2}$

$\iff \sin \left(x+\frac{\pi }{3}\right)=\frac{1}{2}$

$\iff \sin \left(x+\frac{\pi }{3}\right)=\sin \frac{\pi }{6}$

$\iff \sin \left(x+\frac{\pi }{3}\right)=\sin \frac{\pi }{6}$

$\iff \left[\begin{array}{l}x+\frac{\pi }{3}=\frac{\pi }{6}+k2\pi \\ x+\frac{\pi }{3}=\frac{5\pi }{6}+k2\pi \end{array}\right.$

$\iff \left[\begin{array}{l}x=-\frac{\pi }{6}+k2\pi \\ x=\frac{\pi }{2}+k2\pi \end{array}\right.$ với $k\in \mathbb{Z}$

Vậy nghiệm âm lớn nhất của phương trình là  nên ta có:  a = 1, b = 6

Do đó, a + b = 7.

Đáp án đúng là: A

Hàm số y = cosx đồng biến trên mỗi khoảng $(-\pi +k2\pi ;k2\pi )$ với $k\in \mathbb{Z}$

Do đó, trên $\left(\frac{\pi }{5};\frac{4\pi }{3}\right)$, hàm số đồng biến trên khoảng $\left(\pi ;\frac{4\pi }{3}\right)$ . Vậy độ dài khoảng đồng biến là: $\frac{4\pi }{3}-\pi =\frac{\pi }{3}$ .

Đáp án đúng là: B

$\cos x\sin \left(2x-\frac{\pi }{3}\right)=0$

$\iff \left[\begin{array}{l}\cos x=0\\ \sin \left(2x-\frac{\pi }{3}\right)=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{\pi }{2}+k\pi \\ 2x-\frac{\pi }{3}=k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

 $\iff \left[\begin{array}{l}x=\frac{\pi }{2}+k\pi \\ 2x=\frac{\pi }{3}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{2}+k\pi \\ 2x=\frac{\pi }{3}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

Đáp án đúng là: A

${\sin }^{2}x+3\cos x-4=0$

$\iff 1-co{s}^{2}x+3\cos x-4=0$

$\iff -co{s}^{2}x+3\cos x-3=0$

$\iff \cos x\in \varnothing$

Vậy phương trình vô nghiệm.

Đáp án đúng là: C

sin3x – 6 – 5m = 0

$\iff \sin 3x=6+5m$

Phương trình có nghiệm khi và chỉ khi:

$-1\le 6+5m\le 1$

$\iff -7\le 5m\le -5$

$\iff \frac{-7}{5}\le m\le -1$

Đáp án đúng là: B

Gọi M(x; y) là điểm thuộc đường thẳng Δ, M’(x’; y’) là điểm thuộc đường thẳng Δ’

Và M’ là ảnh của M qua $V_{\left(O;-\frac{1}{2}\right)}$ .

Ta có:  $\overrightarrow{OM\text{'}}=-\frac{1}{2}\overrightarrow{OM}\Rightarrow \left\{\begin{array}{l}x\text{'}=-\frac{1}{2}x\\ y\text{'}=-\frac{1}{2}y\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}x=-2x\text{'}\\ y=-2y\text{'}\end{array}\right.$

Do M thuộc Δ nên ta có:

2x – 3y + 8 = 0

⇒ 2(–2x’) – 3(–2y’)  + 8 = 0

⇒ –4x’ + 6 y’ + 8 = 0

⇒ –2x’ + 3y’ + 4 = 0

⇒ 2x’ – 3y’ – 4 = 0

Mà M’ thuộc Δ’ nên ta có phương trình của Δ’ là: 2x – 3y – 4 = 0.

Đáp án đúng là: B

*Lời giải

TH1: Bạn nữ ngồi ghế đầu

Xếp 4 bạn nữ vào 4 vị trí sao cho mỗi bạn cách nhau 1 ghế có 4! cách

Xếp 4 bạn nam vào 4 vị trí còn lại có 4! cách

Vậy có 4!.4! cách

TH2: Bạn nam ngồi ghế đầu

Xếp 4 bạn nam vào 4 vị trí sao cho mỗi bạn cách nhau 1 ghế có 4! cách

Xếp 4 bạn nữ vào 4 vị trí còn lại có 4! cách

Vậy có 4!.4! cách

Vậy số cách xếp mà nam và nữ được xếp xen kẽ nhau là 2.(4!)².

$\to$ B đúng.

*Phương pháp giải

* Sử dụng quy tắc cộng và quy tắc nhân

* Chú ý:

- Bài toán đếm yêu cầu sắp xếp phần tử A và B phải đứng cạnh nhau, ta bó (gộp) 2 phần tử làm 1, coi như chúng là 1 phần tử rồi sắp xếp.

- Bài toán đếm yêu cầu sắp xếp phần tử A và B không đứng cạnh nhau, ta đếm phần bù (Tức là đếm 2 phần tử A và B đứng cạnh nhau).

*Lý thuyết cần nắm thêm về hoán vị

* Hoán vị

1. Định nghĩa

- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.

Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.

2. Số các hoán vị

Kí hiệu: P_n là số các hoán vị của n phần tử.

- Định lí: P_n = n.(n – 1).(n – 2)….2.1

- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: P_n = n!.

- Ví dụ 1. Có bao nhiêu cách xếp 10 học sinh thành một hàng ngang.

Lời giải:

Số cách xếp 10 học sinh thành một hàng ngang là 10! cách.

Xem thêm một số bài viết liên quan hay, chi tiết:

Đáp án đúng là: D

Độ dài bé nhất của $\overrightarrow{u}$  bằng khoảng cách từ một điểm bất kì trên d tới d’

Có: M(0; 1) thuộc đường thẳng d

Ta có: $\left|\overrightarrow{u}\right|=d(M;d\text{'})=\left|\frac{0+1-5}{\sqrt{1+1}}\right|=2\sqrt{2}$ .

Đáp án đúng là: C

Tâm của đường tròn $\left(C_1\right):{(x-3)}^2+{(y+2)}^2=4$  là I’(3; –2) và bán kính R’ = 2

Tâm của đường tròn $\left(C_2\right):{(x+1)}^2+{(y-4)}^2=36$  là I’’(–1; 4) và bán kính R’’=6

Ta có: $k=\frac{-6}{2}=-3$

$\overrightarrow{II\text{'}\text{'}}=-3\overrightarrow{II\text{'}}\Rightarrow \left\{\begin{array}{l}-1-a=-3(3-a)\\ 4-b=-3(-2-b)\end{array}\right.\Rightarrow \left\{\begin{array}{l}-1-a=-9+3a\\ 4-b=6+3b\end{array}\right.\Rightarrow \left\{\begin{array}{l}\text{a=2}\\ b=\frac{-1}{2}\end{array}\right.$

$\Rightarrow a+b=2-\frac{1}{2}=\frac{3}{2}$

Đáp án đúng là: B

Ta có 253 125 000 = 2³ . 3⁴ . 5⁸ nên mỗi ước số tự nhiên của số đó cho đều có dạng

2^m. 3ⁿ . 5^p

Trong đó, ta có: 0 ≤ m ≤ 3; 0 ≤ n ≤ 4; 0 ≤ p ≤ 8

Có 4 cách chọn m

Có 5 cách chọn n

Có 9 cách chọn p

Vậy số ước số tự nhiên là: 4. 5. 9 = 180

Đáp án đúng là: B

$\sin \left(x-\frac{\pi }{3}\right)-\sqrt{3}cos\left(x-\frac{\pi }{3}\right)=2m$

Để phương trình vô nghiệm ta có:

${\left(2m\right)}^2>1^2+{\left(\sqrt{3}\right)}^2$

$\iff 4m^2>4$

$\iff m^2>1$

Số giá trị nguyên của tham số m thuộc đoạn [–10; 10] để phương trình $\sin \left(x-\frac{\pi }{3}\right)-\sqrt{3}cos\left(x-\frac{\pi }{3}\right)=2m$ vô nghiệm  là: 18.

Đáp án đúng là: A

$y=\frac{\sin x+\cos x-1}{\sin x-\cos x+3}$

$\iff y(\sin x-\cos x+3)=\sin x+\cos x-1$

$\iff (y-1)\sin x-(y+1)\cos x=-3y-1\left(1\right)$

Phương trình (1) có nghiệm $\iff {(y-1)}^2+{(y+1)}^2\ge {(-3y-1)}^2$

$\iff 2y^2+2\ge 9y^2+6y+1$

$\iff 7y^2+6y-1\le 0$

$\iff -1\le y\le \frac{1}{7}$

Vậy giá trị lớn nhất của hàm số là $\frac{1}{7}$ .

Đáp án đúng là: A

Xét cosx = 0, ta có 1 + 0  = 2(1 + 0)

Vậy cosx = 0 không là nghiệm của phương trình

Chia cả hai vế phương trình cho $co{s}^{2020}x\ne 0$, ta có:

$\frac{{\sin }^{2018}x}{co{s}^{2020}x}+\frac{co{s}^{2018}x}{co{s}^{2020}x}=2\frac{({\sin }^{2020}x+co{s}^{2020}x)}{co{s}^{2020}x}$

$\iff \frac{1}{co{s}^{2}x.}.{\tan }^{2018}x+\frac{1}{{\cos }^{2}x}=2({\tan }^{2020}x+1)\left(1\right)$

$\iff (1+{\tan }^{2}x).{\tan }^{2018}x+1+{\tan }^{2}x=2({\tan }^{2020}x+1)$

Đặt t = tanx, phương trình trở thành:

$(1+t^2).{\mathrm{t}}^{2018}+1+{\mathrm{t}}^2=2({\mathrm{t}}^{2020}+1)$

$\iff {\mathrm{t}}^{2018}+{\mathrm{t}}^{2020}+1+t^2=2{\mathrm{t}}^{2020}+2$

$\iff {\mathrm{t}}^{2020}+1-{\mathrm{t}}^{2018}-t^2=0$

$\iff {\mathrm{t}}^{2018}(t^2-1)-(t^2-1)=0$

$\iff ({\mathrm{t}}^{2018}-1)(t^2-1)=0$

$\iff \left[\begin{array}{l}{t}^{2018}-1=0\\ t^2-1=0\end{array}\right.$

$\iff \left[\begin{array}{l}{t}^{2018}=1\\ t^2=1\end{array}\right.$

$\iff \left[\begin{array}{l}{t}^{2018}=1\\ t^2=1\end{array}\right.$

$\iff \left[\begin{array}{l}t=1\\ t=-1\end{array}\right.$

$\iff \left[\begin{array}{l}\tan x=1\\ \tan x=-1\end{array}\right.$

 $\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=-\frac{\pi }{4}+k\pi \end{array}\right.$với $k\in \mathbb{Z}$

$\iff x=\frac{\pi }{4}+k\frac{\pi }{2}$ với $k\in \mathbb{Z}$

Với x thuộc khoảng (0; 2018) ta có:

$0<\frac{\pi }{4}+k\frac{\pi }{2}<2018\Rightarrow 0\le k\le 1284$ với $k\in \mathbb{Z}$

Vậy tổng các nghiệm của phương trình trong khoảng (0; 2018) bằng

$\frac{\pi }{4}.1285+(1+2+\mathrm{...}+1284)\frac{\pi }{2}$

$={\left(\frac{1285}{2}\right)}^2\pi$.

Đáp án đúng là: A

$C_x^1+C_x^2-C_x^3=x^2-10x+30$

$\iff \frac{x!}{(x-1)!}+\frac{x!}{2(x-2)!}-\frac{x!}{6(x-3)!}=x^2-10x+30$

$\iff \frac{x!}{(x-1)(x-2)(x-3)!}+\frac{x!}{2(x-2)(x-3)!}-\frac{x!}{6(x-3)!}=x^2-10x+30$

$\iff \frac{6x!}{6(x-1)(x-2)(x-3)!}+\frac{3(x-1)x!}{6(x-1)(x-2)(x-3)!}-\frac{(x-1)(x-2)x!}{6(x-1)(x-2)(x-3)!}=x^2-10x+30$

$\iff \frac{6x!+(3x-3)x!-(x^2-2x-x+2)x!}{6(x-1)(x-2)(x-3)!}=x^2-10x+30$

$\iff \frac{x!\left[6+(3x-3)-(x^2-2x-x+2)\right]}{6(x-1)(x-2)(x-3)!}=x^2-10x+30$

$\iff \frac{x!(6+3x-3-x^2+2x+x-2)}{6(x-1)(x-2)(x-3)!}=x^2-10x+30$

$\iff \frac{x!(-x^2+6x+1)}{6(x-1)(x-2)(x-3)!}=x^2-10x+30$

$\iff \frac{x(x-1)!(-x^2+6x+1)}{6(x-1)!}=x^2-10x+30$

$\iff \frac{x(-x^2+6x+1)}{6}=x^2-10x+30$

$\iff -x^3+6x^2+x=6x^2-60x+180$

$\iff -x^3+6x^2+x=6x^2-60x+180$

$\iff -x^3+61x-180=0$

$\iff \left[\begin{array}{l}x=-9\\ x=5\\ x=4\end{array}\right.$

Đáp án đúng là: D

Gọi số cần lập là $\overline{abcdef}$

Số tự nhiên lẻ nên f có 5 cách chọn

Số cách chọn b, c, d, e là ${10}^4$ cách

Gọi r là số dư khi (b + c + d + e + f) chia cho 9

Để $\overline{abcdef}$ chia hết cho 9 thì r +  9 phải chia hết cho 9

Mà  0 < r + a < 18 ⇒ r + a = 9 ⇒ a = 9 – r

Do đó, a chỉ có 1 cách chọn

Vậy số số tự nhiên lẻ có 6 chữ số và chia hết cho 9 là: 5.${10}^4$.1 = 50000.

Đáp án đúng là: C

m.cosx + 1 = 0

$\iff \cos x=\frac{-1}{m}$

Phương trình có nghiệm khi và chỉ khi

$-1\le \frac{-1}{m}\le 1$

$\iff \left[\begin{array}{l}\frac{-1}{m}\ge -1\\ \frac{-1}{m}\le 1\end{array}\right.\iff \left[\begin{array}{l}m\le -1\\ m\ge 1\end{array}\right.$

Vậy số giá trị nguyên của tham số m thuộc đoạn [–2018; 2018] để phương trình m.cosx + 1 = 0 có nghiệm là: 2018 + 2018 = 4036.

Đáp án đúng là: A

$\frac{\sin 3x}{\cos x+1}=0$

Điều kiện xác định của phương trình là: $\cos x+1\ne 0\Rightarrow \cos x\ne -1\Rightarrow x\ne \pi +k2\pi$

Với điều kiện xác định trên ta có:

$\frac{\sin 3x}{\cos x+1}=0$

$\Rightarrow \sin 3x=0$

$\Rightarrow 3x=k\pi$

$\Rightarrow x=k\frac{\pi }{3}$

Các nghiệm của phương trình thuộc đoạn [2π;4π] là: $\left\{2\pi ;\frac{7}{3}\pi ;\frac{8}{3}\pi ;\frac{10}{3}\pi ;\frac{11}{3}\pi ;4\pi \right\}$

Có tất cả 6 nghiệm.

Đáp án đúng là: D

Xét điểm M(1; –2) thuộc đường đồ thị (P’). Gọi M’(x; y) là ảnh của M qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(0;1)$.

Ta có: $\overrightarrow{MM\text{'}}=\overrightarrow{v}\Rightarrow \left\{\begin{array}{l}x-1=0\\ y+2=1\end{array}\right.\Rightarrow \left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$

Do đó, M’(1; –1)

Do (P) là ảnh của (P’) qua phép tịnh tiến theo vectơ  nên ta có M’ thuộc parabol (P), ta có:

$-1=-1^2-2.1+m$

$\iff m=2$

Đáp án đúng là: C

Tọa độ của A và B là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}{(x+2)}^2+{(y-1)}^2=4\\ x-y+2=0\end{array}\right.$

$\iff \left\{\begin{array}{l}{(x+2)}^2+{(y-1)}^2=4\\ y=x+2\end{array}\right.$

$\iff \left\{\begin{array}{l}{(x+2)}^2+{(x +2-1)}^2=4\\ y=x+2\end{array}\right.$

$\iff \left\{\begin{array}{l}{(x+2)}^2+{(x+1)}^2=4\\ y=x+2\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}^2+4x+4+x^2+2x+1=4\\ y=x+2\end{array}\right.$

$\iff \left\{\begin{array}{l}2x^2+6x+1=0\\ y=x+2\end{array}\right.$

$\iff \left\{\begin{array}{l}\left[\begin{array}{l}x=\frac{-3+\sqrt{7}}{2}\\ x=\frac{-3-\sqrt{7}}{2}\end{array}\right.\\ y=x+2\end{array}\right.$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{-3+\sqrt{7}}{2}\\ y=\frac{1+\sqrt{7}}{2}\end{array}\right.\\ \left\{\begin{array}{l}x=\frac{-3-\sqrt{7}}{2}\\ y=\frac{1-\sqrt{7}}{2}\end{array}\right.\end{array}\right.$

Vậy tọa độ hai điểm A và B là: $A\left(\frac{-3+\sqrt{7}}{2};\frac{1+\sqrt{7}}{2}\right)$  và $B\left(\frac{-3-\sqrt{7}}{2};\frac{1-\sqrt{7}}{2}\right)$

Tọa độ trung điểm M$\left(x_M;y_M\right)$ của AB là:

$x_M=\frac{\frac{-3+\sqrt{7}}{2}+\frac{-3-\sqrt{7}}{2}}{2}=\frac{-3}{2}$

$y_M=\frac{\frac{1+\sqrt{7}}{2}+\frac{1-\sqrt{7}}{2}}{2}=\frac{1}{2}$

Vì M’(x; y) là ảnh của M qua phép vị tự tâm O tỉ số k = 3 nên ta có: 

$\overrightarrow{OM\text{'}}=3\overrightarrow{OM}\Rightarrow \left\{\begin{array}{l}x=3.\frac{-3}{2}\\ y=3.\frac{1}{2}\end{array}\right.\Rightarrow \left\{\begin{array}{l}x=\frac{-9}{2}\\ y=\frac{3}{2}\end{array}\right.$

Vậy M’ .$\left(-\frac{9}{2};\frac{3}{2}\right)$

$u_{n+1}-u_n=\frac{1}{x_n\sqrt{x_{n+1}}+x_{n+1}\sqrt{x_n}}=\frac{1}{\sqrt{x_n.x_{n+1}}\left(\sqrt{x_n}+\sqrt{x_{n+1}}\right)}=\frac{\sqrt{x_{n+1}}-\sqrt{x_n}}{d\sqrt{x_{n+1}{x}_n}}$

$=\frac{1}{d}\left(\frac{1}{\sqrt{x_n}}-\frac{1}{\sqrt{x_{n+1}}}\right)$

$\Rightarrow u_n=u_1+\frac{1}{d}\left(\frac{1}{\sqrt{x_1}}-\frac{1}{\sqrt{x_n}}\right)$

Ta có: $x_n=1+3(n-1)$

$\underset{n\to +\infty }{\lim }\frac{1}{\sqrt{x_n}}=\underset{n\to +\infty }{\lim }\frac{1}{\sqrt{1+3(n-1)}}=0$

$\Rightarrow \underset{n\to +\infty }{\lim }{u}_n=u_1+\frac{1}{d\sqrt{x_1}}=\frac{2}{3}+\frac{1}{3}=1$.

Đường tròn $\left(C_1\right):x^2+y^2-2x-3=0$ có tâm I(1; 0), bán kính $R=\sqrt{1^2-(-3)}=2$

Đường tròn $\left(C_2\right):x^2+y^2+4x-8y+4=0$  có tâm I’(–2; 4), bán kính $R\text{'}=\sqrt{2^2+4^2-4}=4$

Ta có: $II\text{'}=\sqrt{{(-2-1)}^2+{(4-0)}^2}=5$

Do đó: R’ – R < II’ < R’ + R nên hai đường tròn cắt nhau

Gọi E là các tâm vị tự của hai đường tròn thì ta có:

$\overrightarrow{EI\text{'}}=\pm 2\overrightarrow{EI}$

$\iff \left[\begin{array}{l}\overrightarrow{EI\text{'}}-2\overrightarrow{EI}=0\\ \overrightarrow{EI\text{'}}+2\overrightarrow{EI}=0\end{array}\right.$

$\iff \left[\begin{array}{l}E=\frac{2I-I\text{'}}{3}\\ E=\frac{2I+I\text{'}}{5}\end{array}\right.$

Gọi E(x; y) có:

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{2.1+2}{3}=\frac{4}{3}\\ y=\frac{2.0-4}{3}=\frac{-4}{3}\end{array}\right.\\ \left\{\begin{array}{l}x=\frac{2.1-2}{5}=0\\ y=\frac{2.0+4}{5}=\frac{4}{5}\end{array}\right.\end{array}\right.$

Vậy hai tâm vị tự của hai đường tròn là: $\left(\frac{4}{3};-\frac{4}{3}\right);\left(0;\frac{4}{5}\right)$ .

a) Mỗi hình chữ nhật có hai đường chéo là các đường chéo đi qua tâm của đa giác. Đa giác đều 2022 đỉnh có 1011 đường chéo qua tâm, do đó, số hình chữ nhật là $C_{1011}^2$

b) Gọi $A_1,A_2\mathrm{,...,}{A}_{2022}$  là các đỉnh của đa giác đều 2022 đỉnh

Gọi (O) là đường tròn ngoại tiếp đa giác đều $A_1,A_2\mathrm{,...,}{A}_{2022}$

Các đỉnh của đa giác đều chia (O) thành 2022 cung tròn bằng nhau, mỗi cung tròn có số đo bằng $\frac{360°}{2022}$

Vì tam giác cần đếm có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp của (O) .

Suy ra góc lớn hơn 100° sẽ chắn cung có số đo lớn hơn 200° .

Cố định một đỉnh $A_i$ . Có 2022 cách chọn $A_i$

Gọi $A_i,A_j,A_k$  là các đỉnh sắp thứ tự theo chiều kim đồng hồ sao cho $\stackrel{⏜}{A_i{A}_k}<160°$ thì $\widehat{A_i{A}_j{A}_k}>100°$  và tam giác $A_i{A}_j{A}_k$  là tam giác cần đếm

Khi đó $\stackrel{⏜}{A_i{A}_k}$  là hợp liên tiếp của nhiều nhất $\frac{160}{\frac{360}{2022}}=898$  cung tròn nói trên

898 cung tròn này có 899 đỉnh. Trừ đi đỉnh $A_i$  thì còn 898 đỉnh. Do đó có $C_{898}^2$ cách chọn hai đỉnh $A_j,A_k$ . Vậy có tất cả 2022.$C_{898}^2$  tam giác thỏa mãn yêu cầu bài toán.