Tập xác định của hàm số $y=\frac{1}{\sin 2x+1}$  là:

Đáp án đúng là: C

Lời giải

Điều kiện xác định của hàm số $y=\frac{1}{\sin 2x+1}$ là:

$\sin 2x+1\ne 0$

$\iff \sin 2x\ne -1$

$\iff \sin 2x\ne \sin \frac{-\pi }{2}$

$\iff \left\{\begin{array}{l}2x\ne \frac{-\pi }{2}+k2\pi \\ 2x\ne \frac{3\pi }{2}+k2\pi \end{array}\right.$ với $k\in \mathbb{Z}$

$\iff \left\{\begin{array}{l}x\ne \frac{-\pi }{4}+k\pi \\ x\ne \frac{3\pi }{4}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

$\iff \left\{\begin{array}{l}x\ne \frac{-\pi }{4}+k\pi \\ x\ne \frac{3\pi }{4}+k\pi \end{array}\right.$ với $k\in \mathbb{Z}$

Vậy tập xác định của hàm số $y=\frac{1}{\sin 2x+1}$  là $D=ℝ\backslash \left\{-\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\right\}$ .

*Phương pháp giải:

Hàm phân thức xác định khi và chỉ khi mẫu khác 0

*Lý thuyết:

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

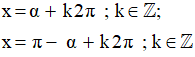
Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}\frac{-\pi }{2}\le \alpha \le \frac{\pi }{2}\\ \sin \alpha =a\end{array}\right.$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

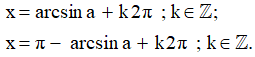
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi$ và $x=\pi -\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$

Tổng quát: 

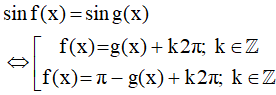
b) Phương trình sinx = sinβ⁰ có các nghiệm là:

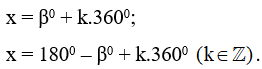
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x=-\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = 0:  Phương trình sinx = 0 có các nghiệm là $x=k\pi ;k\in \mathbb{Z}$.

2. Phương trình cosx = a.

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $\left|\text{cosx }\right|\le 1$ với mọi x.

- Trường hợp $\left|\text{\hspace{0.17em}a }\right|\le 1$.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x=\pm \alpha +k2\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: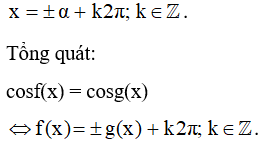 

b) Phương trình cos x= cosβ⁰ có các nghiệm là $x=\pm {\beta }^0+\text{\hspace{0.17em}}k{360}^0;k\in \mathbb{Z}$

c) Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}0\le \alpha \le \pi \\ \cos \alpha =a\end{array}\right.$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

$x=\pm \arccos a\text{\hspace{0.17em}}+k2\pi ;k\in \mathbb{Z}$

d) Các trường hợp đặc biệt:

+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: $x=k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là: $x=\pi +k2\pi ;k\in \mathbb{Z}$

+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới  + Bài Tập) – Toán 11 

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án ) – Toán 11