Đề thi Toán 11 giữa kì 1 có đáp án (đề 5)
-
4475 lượt thi
-
31 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Các hàm số y = sinx, y = cosx, y = tanx, y = cotx, có bao nhiêu hàm số tuần hoàn với chu kì π
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Các hàm số tuần hoàn với chu kì π là y = tanx, y = cotx
Vậy có 2 hàm số tuần hoàn với chu kì π
Câu 2:
17/07/2024Trong các hàm số sau, hàm số nào là hàm số chẵn ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét hàm số y = cosx ta có:
f(x) = cosx
f(–x) = cos(–x) = cosx
Do đó, f(x) = f(–x)
Vậy hàm số y = cosx là hàm số chẵn.
Câu 3:
03/12/2024Tập xác định của hàm số y = cosx là tập hợp nào trong các tập hợp dưới đây ?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
* Lời giải:
Tập xác định của hàm số y = cosx là tập số thực
*Phương pháp giải:
- tìm điều kiện xác định cho hàm cosx
* Lý thuyết và các dạng bài cần nắm thêm về hàm số lượng giác:
a. Hàm số y = sinx
- Tập xác định: D = R
- Tập giá trị: [-1;1]
b. Hàm số y = cosx
- Tập xác định: D = R
- Tập giá trị: [-1;1]
c. Hàm số y = tanx
- Tập xác định:
- Tập giá trị: R
d. Hàm số y = cotx
- Tập xác định:
- Tập giá trị: R
Dạng 1. Tìm tập xác định của hàm số lượng giác
- Phương pháp giải:
xác định khi
xác định khi
xác định khi g(x) > 0
y = tan[u(x)] xác định khi
y = cot[u(x)] xác định khi
khi
khi
- Phương pháp giải:
Sử dụng tính bị chặn của hàm số lượng giác
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của góc lượng giác – Toán 11 Kết nối tri thức
Trắc nghiệm Giá trị lượng giác của góc lượng giác (Kết nối tri thức) có đáp án - Toán 11
Câu 4:
13/12/2024Tìm tập giá trị của hàm số y = cotx?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tìm tập giá trị của hàm số y = cotx là
Phương pháp giải:
Tập xác định của hàm số y = f(x) là tập các giá trị của x sao cho biểu thức f(x) có nghĩa
* Kiến thức mở rộng
* Tập xác định của hàm số lượng giác
– Hàm số y = sin x, y = cos x xác định trên ℝ.
Khi đó, y = sin[u(x)], y = cos [u(x)] xác định khi và chỉ khi u(x) xác định.
– Hàm số y = tan x có tập xác định là 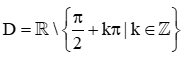
Khi đó, y = tan [u(x)] có nghĩa khi và chỉ khi u(x) xác định và .
– Hàm số y = cot x có tập xác định là D = ℝ \ {kπ | k ∈ ℤ}.
Khi đó, y = cot [u(x)] có nghĩa khi và chỉ khi u(x) xác định và u(x) ≠kπ, k ∈ ℤ.
* Một số chú ý khi tìm điều kiện xác định:
– Hàm số xác định khi f(x) ≥ 0.
– Hàm số xác định khi f(x) ≠ 0.
– Hàm số xác định khi f(x) > 0.
– Một số trường hợp đặc biệt:
;
;
;
;
.
Câu 5:
23/07/2024Tìm tập xác định của hàm số
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điều kiện xác định của hàm số là:
với
Vậy tập xác định của hàm số là D =
Câu 6:
23/07/2024Gọi M và m lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 2cos2x + 3. Tính tổng M + m ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
Vậy M = 1, m = 5 và M + m = 1 + 5 = 6.
Câu 7:
15/10/2024Trong các hàm số sau, hàm số nào là hàm số chẵn ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
*Phương pháp giải
Sử dụng định nghĩa
Hàm số y = f(x) xác định trên D
+ Hàm số chẵn
+ Hàm số lẻ
Chú ý: Một hàm số có thể không chẵn cũng không lẻ
Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng
* Quy trình xét hàm số chẵn, lẻ.
B1: Tìm tập xác định của hàm số.
B2: Kiểm tra
Nếu ∀ x ∈ D ⇒ -x ∈ D Chuyển qua bước ba
Nếu ∃ x0 ∈ D ⇒ -x0 ∉ D kết luận hàm không chẵn cũng không lẻ.
B3: xác định f(-x) và so sánh với f(x).
Nếu bằng nhau thì kết luận hàm số là chẵn
Nếu đối nhau thì kết luận hàm số là lẻ
Nếu tồn tại một giá trị ∃ x0 ∈ D mà f(-x0 ) ≠ ± f(x0) kết luận hàm số không chẵn cũng không lẻ.
*Lời giải
Xét hàm số: y = cotx.sinx = = cosx (với sinx ≠ 0)
Ta có:
f(x) = cosx
f(–x) = cos(–x) = cosx
Do đó, f(x) = f(–x) nên hàm số y = cotx.sinx là hàm số chẵn.
Xem thêm các bài viết liên quan hay, chi tiết:
Phương pháp xét tính chẵn, lẻ của hàm số chi tiết nhất
Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác và cách giải
Câu 15:
07/12/2024Tìm tất cả các giá trị thực của m để phương trình sinx = m vô nghiệm ?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Vì nên phương trình sinx = m vô nghiệm khi chỉ khi
*Phương pháp giải
Nắm vững lý thuyết và cách giải bài toán phương trình lượng giác
*Một số lý thuyết nắm thêm về phương trình lượng giác
1. Phương trình sinx = a.
Xét phương trình sinx = a (1)
- Trường hợp |a| > 1
Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.
- Trường hợp |a| ≤ 1
Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:
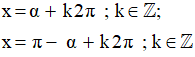
Nếu số thực α thỏa mãn điều kiện: thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:
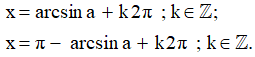
- Chú ý:
a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:
và
Tổng quát:
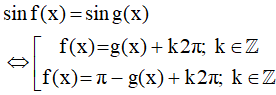
b) Phương trình sinx = sinβ0 có các nghiệm là:
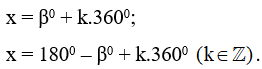
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.
d) Các trường hợp đặc biệt:
+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là .
+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là .
+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là .
Phương trình cosx = a.
- Trường hợp |a| > 1
Phương trình cosx = a vô nghiệm vì với mọi x.
- Trường hợp .
Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:
- Chú ý:
a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: 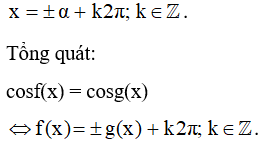
b) Phương trình cos x= cosβ0 có các nghiệm là
c) Nếu số thực α thỏa mãn điều kiện: thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:
d) Các trường hợp đặc biệt:
+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: .
+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là:
+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: .
Xem thêm các bài viết hay, chi tiết khác:
Lý thuyết Phương trình lượng giác cơ bản (mới 2023 + Bài Tập) – Toán 11
Toán 11 Bài 4 (Kết nối tri thức): Phương trình lượng giác cơ bản
Câu 16:
23/07/2024Phương trình nào sau đây vô nghiệm ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét phương trình cosx – 3 = 0 ta có:
cosx – 3 = 0
Mà nên phương trình vô nghiệm.
Câu 17:
17/07/2024Đặt t = sinx với điều kiện , phương trình trở thành phương trình nào dưới đây ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đặt t = sinx với điều kiện , phương trình trở thành:
Câu 19:
18/07/2024Phương trình tương đương với phương trình nào sau đây
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Câu 20:
17/07/2024Trong mặt phẳng Oxy, cho điểm M’(x’; y’) là ảnh của điểm M(x; y) qua phép tịnh tiến theo vectơ . Tìm mệnh đề đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trong mặt phẳng Oxy, cho điểm M’(x’; y’) là ảnh của điểm M(x; y) qua phép tịnh tiến theo vectơ .
Ta có:
Câu 21:
23/07/2024Cho hình chữ nhật MNPQ. Tìm ảnh của điểm Q qua phép tịnh tiến theo vectơ
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
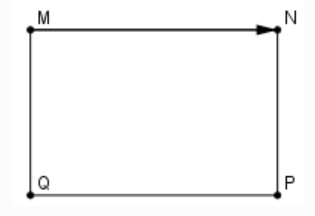
Ta có:
Ảnh của điểm Q qua phép tịnh tiến theo vectơ là P .
Câu 22:
17/07/2024Trong mặt phẳng tọa độ Oxy, cho điểm M(1; –3). Ảnh của điểm M qua phép tịnh tiến theo vectơ là.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi M(x; y) là ảnh của điểm M qua phép tịnh tiến theo vectơ
Ta có:
Câu 23:
21/07/2024Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x + 2y – 6 = 0. Ảnh của đường thẳng d qua phép tịnh tiến theo là đường thẳng d’ có phương trình
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ảnh của đường thẳng d qua phép tịnh tiến theo là đường thẳng d’ có phương trình dạng 3x + 2y + c = 0
Cho là điểm thuộc đường thẳng d
Ảnh M’(x; y) của M qua phép tịnh tiến theo
Ta có:
Mà M’ thuộc d’ nên ta có:
Vậy phương trình của d’ là: 3x + 2y – 9 = 0
Câu 24:
21/07/2024Cho phép quay biến điểm M thành M’. Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phép quay biến điểm M thành M’ nên ta có: và
Câu 25:
17/07/2024Trong hệ tọa độ Oxy, cho điểm A(1; 0). Ảnh của A qua phép quay tâm O, góc quay là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi A’(x; y) là ảnh của A qua phép quay tâm O, góc quay
Ta có:
Câu 26:
19/07/2024Phép quay biến đường tròn (C) có bán kính R thành đường tròn (C’) có bán kính R’. Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phép quay biến đường tròn (C) có bán kính R thành đường tròn (C’) có bán kính R’. Do Phép quay biến đường tròn thành đường tròn có cùng bán kính. Nên ta có: R = R’
Câu 27:
17/07/2024Trong hệ tọa độ Oxy, phép quay tâm O góc quay biến M(–3; 5) thành điểm nào ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi M’(x; y) là ảnh của M qua phép quay tâm O, góc quay
Ta có:
Câu 28:
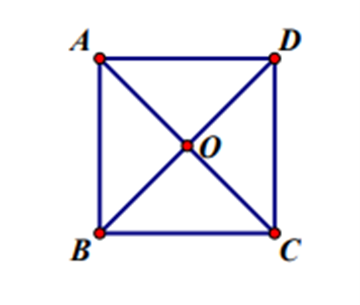
23/07/2024Cho hình vuông ABCD tâm O. Xác định ảnh của tam giác OBC qua phép quay tâm O góc quay ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta thấy, phép quay tâm O góc quay biến điểm B thành điểm A, biến điểm C thành điểm B. Do đó, ảnh của tam giác OBC qua phép quay tâm O góc quay là tam giác OAB
Câu 29:
23/07/2024Tìm tập xác định của hàm số .
 Xem đáp án
Xem đáp án
Ta có:
Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số là .
Câu 30:
17/07/2024Giải các phương trình lượng giác sau:
a) ;
b) .
 Xem đáp án
Xem đáp án
a)
với
với
với
Vậy tập nghiệm của phương trình là: .
b)
với
Vậy tập nghiệm của phương trình là: .
Câu 31:
17/07/2024Trong mặt phẳng Oxy, cho đường tròn (C): và . Viết phương trình đường tròn (C’) biết (C’) là ảnh của (C) qua phép tịnh tiến theo vectơ .
 Xem đáp án
Xem đáp án
Xét đường tròn (C): có tâm I(–3; 1) và bán kính R =
Gọi đường tròn (C’) có tâm I’(x; y), bán kính R’ =
Ta có:
Vậy phương trình đường tròn (C’) là: .
Bài thi liên quan
-
Đề thi Toán 11 giữa kì 1 có đáp án (đề 1)
-
33 câu hỏi
-
90 phút
-
-
Đề thi Toán 11 giữa kì 1 có đáp án (đề 2)
-
31 câu hỏi
-
90 phút
-
-
Đề thi Toán 11 giữa kì 1 có đáp án (đề 3)
-
30 câu hỏi
-
90 phút
-
-
Đề thi Toán 11 giữa kì 1 có đáp án (đề 4)
-
25 câu hỏi
-
90 phút
-
-
Đề thi Toán 11 giữa kì 1 có đáp án (đề 6)
-
6 câu hỏi
-
60 phút
-
Có thể bạn quan tâm
- Đề thi Toán 11 giữa kì 1 có đáp án (4474 lượt thi)
- Đề thi Học kì 1 Toán lớp 11 năm 2020 - 2021 có đáp án (880 lượt thi)
- Đề thi Toán 11 Học kì 1 có đáp án (886 lượt thi)
Các bài thi hot trong chương
- Đề thi Toán 11 Học kì 2 có đáp án (1244 lượt thi)
- Đề thi Học kì 2 Toán 11 có đáp án (915 lượt thi)
