Câu hỏi:
17/07/2024 203Giải các phương trình lượng giác sau:
a) sin3x+cos3x=√2cos2x;
b) (2sinx−cosx)(1+cosx)=sin2x.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) sin3x+cos3x=√2cos2x
⇔1√2sin3x+1√2cos3x=cos2x
⇔cosπ4sin3x+sinπ4cos3x=sin(π2−2x)
⇔sin(3x+π4)=sin(π2−2x)
⇔[3x+π4=π2−2x+k2π3x+π4=π−π2+2x+k2π với k∈ℤ
⇔[5x=π4+k2πx=π4+k2πvới k∈ℤ
⇔[x=π20+k2π5x=π4+k2π với k∈ℤ
Vậy tập nghiệm của phương trình là: S={π20+k2π5;π4+k2π|k∈ℤ}.
b)
(2sinx−cosx)(1+cosx)=sin2x
⇔2sinx+2sinxcosx−cosx−cos2x=sin2x
⇔2sinx+2sinxcosx−cosx−cos2x−sin2x=0
⇔(2sinx+2sinxcosx)−(cosx+cos2x+sin2x)=0
⇔(2sinx+2sinxcosx)−(cosx+cos2x+sin2x)=0
⇔2sinx(1+cosx)−(cosx+1)=0
⇔(2sinx−1)(1+cosx)=0
⇔[2sinx−1=01+cosx=0
⇔[sinx=12cosx=−1
⇔[sinx=sinπ6cosx=cosπ
⇔[x=π6+k2πx=5π6+k2πx=π+k2π
⇔[x=π6+k2πx=5π6+k2πx=π+k2π với k∈ℤ
Vậy tập nghiệm của phương trình là: S={π6+k2π;5π6+k2π;π+k2π|k∈ℤ}.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tìm tất cả các giá trị thực của m để phương trình sinx = m vô nghiệm ?
Câu 3:
Gọi M và m lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 2cos2x + 3. Tính tổng M + m ?
Câu 5:
Tập xác định của hàm số y = cosx là tập hợp nào trong các tập hợp dưới đây ?
Câu 10:
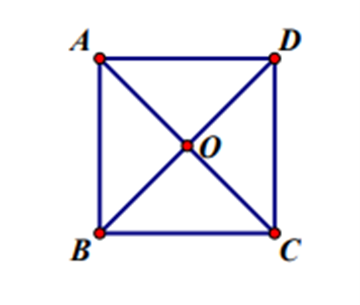
Cho hình vuông ABCD tâm O. Xác định ảnh của tam giác OBC qua phép quay tâm O góc quay ?
Câu 13:
Phép quay biến đường tròn (C) có bán kính R thành đường tròn (C’) có bán kính R’. Khẳng định nào sau đây là đúng ?
Câu 15:
Các hàm số y = sinx, y = cosx, y = tanx, y = cotx, có bao nhiêu hàm số tuần hoàn với chu kì π


