Trắc nghiệm Toán 11 Bài 5: Khoảng cách
-
1076 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
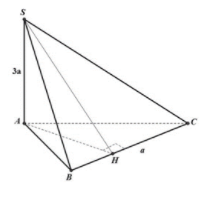
Kẻ AH vuông góc với BC
SΔABC=12AH.BC
→AH=2.SΔABCBC
=4a2a=4a
Khoảng cách từ S đến BC chính là SH
Dựa vào tam giác vuông ΔSAH ta có
SH=√SA2+AH2
=√(3a)2+(4a)2=5a
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
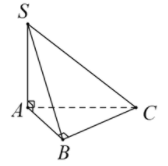
Do {SA⊥ABSA⊥BC nên SA⊥(ABC)
⇒SA⊥AC
Như vậy SC=√SA2+AC2
=√SA2+(AB2+BC2)=√3
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
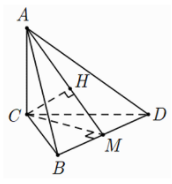
Do ΔABC đều cạnh a nên đường cao MC=a√32
d(C,AM)=CH
=AC.MC√AC2+MC2=a√6611
Câu 4:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
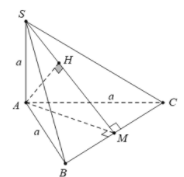
Gọi M là trung điểm của BC; H là hình chiếu vuông góc của A trên SM.
Ta có BC⊥AM và BC⊥SA nên
BC⊥(SAM)⇒BC⊥AH.
Mà AH⊥SM, do đó AH⊥(SBC).
Vậy AH=d(A,(SBC)).
AM=a√32;
AH=AS.AM√AS2+AM2=a√217.
Câu 5:
29/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Lời giải:
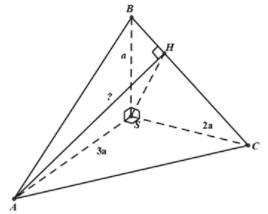
+ Dựng AH⊥BC ⇒d(A,BC)=AH
+ {AS⊥(SBC)⊃BC⇒AS⊥BCAH⊥BC
AH cắt Á cùng nằm trong (SAH).
⇒BC⊥(SAH)⊃SH⇒BC⊥SH
Xét trong ΔSBC vuông tại S có H là đường cao ta có:
1SH2=1SB2+1SC2
=1a2+14a2=54a2
⇒SH2=4a25
⇒SH=2a√55
+ Ta dễ chứng minh được AS⊥(SBC)⊃SH⇒AS⊥SH
⇒ΔASH vuông tại S.
Áp dụng hệ thức lượng trong ΔASH vuông tại S ta có:
AH2=SA2+SH2
=9a2+4a25=49a25
⇒AH=7a√55
*Phương pháp giải:
Sử dụng phương pháp tính khoảng cách từ đường thẳng tới mặt phẳng
*Lý thuyết:
1. Khoảng cách từ một điểm đến một đường thẳng
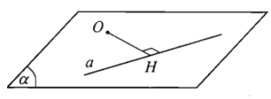
Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.
Kí hiệu: d(O; a).
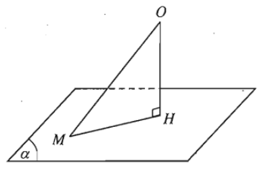
2. Khoảng cách từ một điểm đến một mặt phẳng
Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).
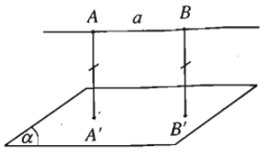
1. Khoảng cách giữa đường thẳng và măt phẳng song song.
- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).
Kí hiệu là d(a; (α)) .
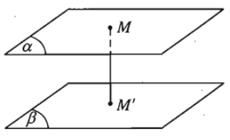
2. Khoảng cách giữa hai mặt phẳng song song.
- Định nghĩa: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.
- Kí hiệu: d((α); (β)).
Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).
Xem thêm
Lý thuyết Khoảng cách (mới + Bài Tập) - Toán 11Câu 6:
18/07/2024Cho hình chóp S.ABCD có SA⊥( ABCD), mặt đáy ABCD là hình thang vuông có chiều cao AB=a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
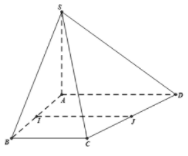
SA⊥(ABCD)⇒SA⊥AI
Lại có AI⊥AD ( hình thang vuông)
suy ra IA⊥(SAD)
IJ∥AD theo tính chất hình thang, nên
d(IJ,(SAD))=d(I,(SAD))
=IA=a2
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
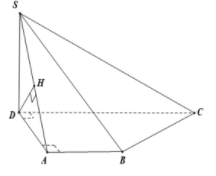
Trong tam giác DHA , dựng DH⊥SA;
Vì DC//AB
⇒d(DC;(SAB))=d(D;(SAB))
=DH
Xét tam giác vuông SDA có :
1DH2=1SD2+1AD2
⇒DH=a√123=2a√3
Câu 8:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
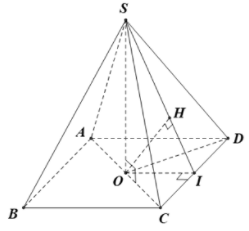
Gọi O là tâm hình vuông ABCD
Khi đó SO⊥(ABCD)
Kẻ OI⊥CD, OH⊥SI
⇒OH⊥(SCD)
Ta tính được AO=a√22,
Câu 9:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
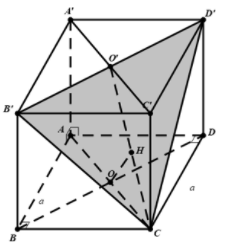
Gắn hệ trục tọa độ như hình vẽ
Viết phương trình mặt phẳng
Có VTPT
Vậy .
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
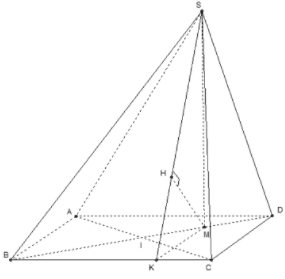
Đặc điểm của hình: Góc giữa SB tạo với mặt phẳng là
;
Xác định khoảng cách:
Tính khoảng cách MH:
.vậy
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
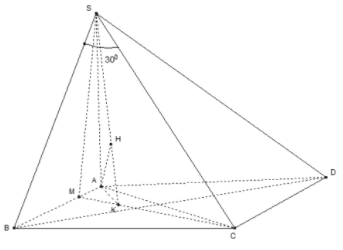
Đặc điểm của hình: SC tạo với mặt phẳng góc
; ; ;
;; ;
Xác định khoảng cách:
Tính
Vậy
Câu 12:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
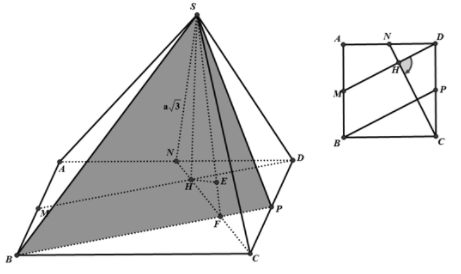
Ta chứng minh:
Thật vậy: vì
mà
Ta có:
Kẻ
Do
Mà .
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
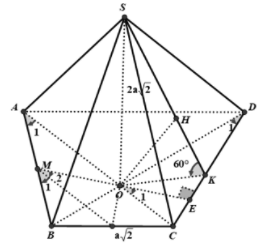
Do
Dựng góc giữa :
. Kẻ
Kéo dài MO cắt DC tại E
Ta có:
Ta có:
.
Câu 15:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Đáp án A: Đúng
Đáp án B: Sai, do phát biểu này thiếu yếu tố cắt nhau.
Đáp án C: Sai, vì mặt phẳng đó chưa chắc đã tồn tại.
Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc.
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
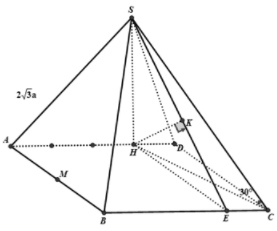
SC có hình chiếu vuông góc lên mp là HC
Đặt
Ta có :
Mà :
Kẻ
Kẻ
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
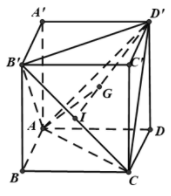
Ta có:
Nên tứ diện là tứ diện đều.
Gọi I là trung điểm , G là trọng tâm tam giác .
Khi đó ta có:
Vì tam giác đều nên
.
Theo tính chất trọng tâm ta có:
.
Trong tam giác vuông có:
.
Câu 19:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
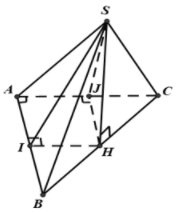
Gọi H là hình chiếu của S lên , vì mặt bên vuông góc với nên
Dựng , theo đề bài ta có
Do đó tam giác (cạnh góc vuông - góc nhọn)
Suy ra .
Lại có
Vậy H trùng với trung điểm của BC.
Từ đó ta có HI là đường trung bình của tam giác ABC nên .
Tam giác SHI vuông tại H và có
vuông cân.
Do đó: .
Câu 20:
20/07/2024Cho hình chóp tam giác đều S.ABC có cạnh bên bằng b, cạnh đáy bằng d, với Hãy chọn khẳng định đúng trong các khẳng định bên dưới.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
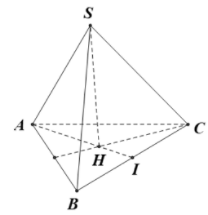
Gọi I là trung điểm của BC, H là trọng tâm tam giác ABC.
Do S.ABC là hình chóp đều nên
Ta có
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
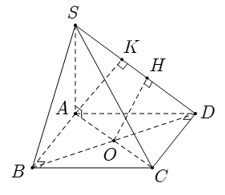
Nếu
(vì
có 2 góc vuông (vô lý).
Theo tính chất của hình vuông .
Nếu
có 2 góc vuông (vô lý)
Như vậy
Câu 22:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
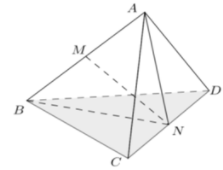
Gọi M, N lần lượt là trung điểm của AB và CD.
Khi đó nên tam giác ANB cân, suy ra .
Chứng minh tương tự ta có , nên .
Ta có:
(p là nửa chu vi)
Mặt khác:
Cách khác. Tính
.
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
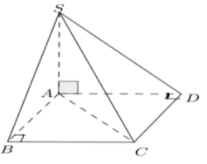
Ta có: BC //
Mà
Ta có:
Câu 24:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
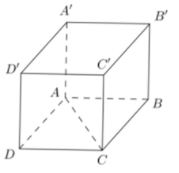
Ta có:
Câu 25:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
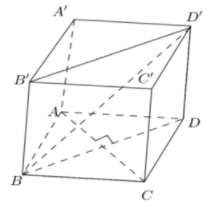
Ta có:
Câu 26:
25/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải:
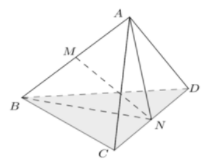
Gọi M, N lần lượt là trung điểm của AB và CD.
Khi đó nên tam giác ANB cân, suy ra .
Chứng minh tương tự ta có , nên .
Ta có:
(p là nửa chu vi)
Mặt khác:
*Phương pháp giải:
1.Gọi M,I lần lượt là trung điểm là CD và AB.Chứng minhd(AB,CD)=MI
2.Tính MI
*Lý thuyết:
Trong không gian tọa đọ Oxyz, có 4 vị trí tương đối của 2 đường thẳng đó là trùng nhau, cắt nhau, chéo nhau và song song. Trong trường hợp 2 đường thẳng chéo nhau, khoảng cách giữa chúng là độ dài đoạn vuông góc chung của 2 đường thẳng. Trong đó, đoạn thẳng nối 2 điểm trên 2 đường thẳng chéo nhau, đồng thời vuông góc với cả 2 đường thẳng đó chính là đoạn vuông góc chung.
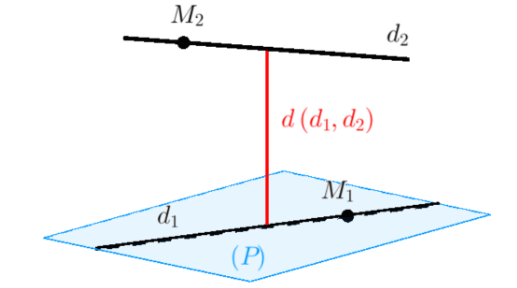
Lưu ý, đoạn vuông góc chung của 2 đường thẳng chéo nhau là chỉ có một và tồn tại duy nhất.
2. Phương pháp tính khoảng cách giữa 2 đường thẳng chéo nhau
Để có thể tính được khoảng cách giữa 2 đường thẳng chéo nhau thì chúng ta có thể sử dụng một trong các cách dưới đây:
Phương pháp 1: Dựng đoạn vuông góc chung MN của a và b, khi đó d (a,b) = MN.
Tuy nhiên, khi dựng đoạn vuông góc chung MN, chúng ta có thể sẽ gặp phải các trường hợp sau:
- Trường hợp 1: ∆ và ∆’ vừa chéo vừa vuông góc với nhau
Khi gặp trường hợp này, chúng ta sẽ làm như sau:
- Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
- Bước 2: Trong mặt phẳng (α) kẻ đường thẳng IJ vuông góc với ∆’
Khi đó IJ chính là đoạn vuông góc chung và d (∆, ∆’) = IJ.
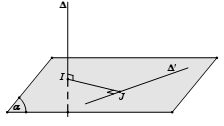
- Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau
- Bước 1: Bạn chọn một mặt phẳng (α) chứa ∆’ và song song với ∆
- Bước 2: Bạn dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M thuộc ∆ dựng đoạn MN vuông góc với (α) . Khi đó, d sẽ là đường thẳng đi qua N và song song với ∆
- Bước 3: Bạn gọi H là giao điểm của đường thẳng d với ∆’, dựng HK // MN
Khi đó, HK chính là đoạn vuông góc chung và d (∆, ∆’) = HK = MN.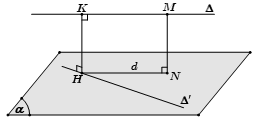
Hoặc bạn làm như sau:
- Bước 1: Chọn mặt phẳng (α) vuông góc với ∆ tại I
- Bước 2: Bạn tìm hình chiếu d của ∆’ xuống mặt phẳng (α)
- Bước 3: Trong mặt phẳng (α), dựng IJ vuông góc với d, từ J bạn dựng đường thẳng song song với ∆ và cắt ∆’ tại H, từ H dựng HM // IJ
Khi đó, HM chính là đoạn vuông góc chung và d (∆, ∆’) = HM = IJ.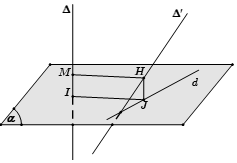
Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó, d (∆, ∆’) = d (∆’, (α)).
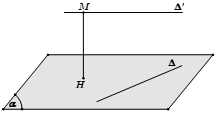
Phương pháp 3: Dựng 2 mặt phẳng song song và lần lượt chứa 2 đường thẳng. Khoảng cách giữa 2 mặt phẳng đó chính là khoảng cách giữa 2 đường thẳng cần tìm.
Lưu ý: Phương pháp này thường sử dụng trong trường hợp khi kẻ đường thẳng song song với 1 trong 2 đường đề bài cho ban đầu gặp khó khăn.
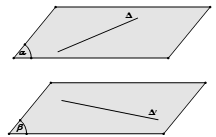
Phương pháp 4: Sử dụng phương pháp vec tơ
* MN là đoạn vuông góc chung của AB và CD khi và chỉ khi:
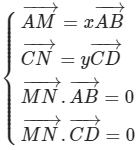
* Nếu trong mặt phẳng (α) có hai véc tơ không cùng phương thì:
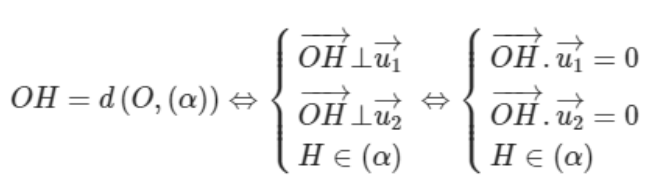
Xem thêm
Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập
Câu 27:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
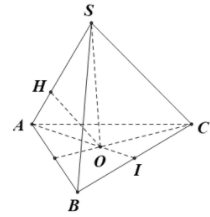
Vì hình chóp S.ABC đều có SO là đường cao
O là tâm của
Gọi I là trung điểm cạnh BC.
Tam giác ABC đều nên
.
Kẻ
Xét tam giác SOA vuông tại O :
Câu 28:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
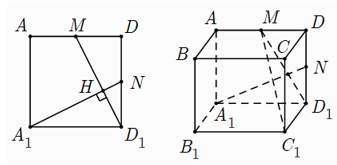
Gọi N là trung điểm cạnh và
Khi đó ta chứng minh được
suy ra
Câu 29:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
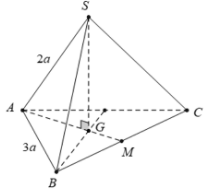
Gọi G là trọng tâm tam giác ABC. Do S.ABC là chóp đều nên .
vuông tại G
Câu 30:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
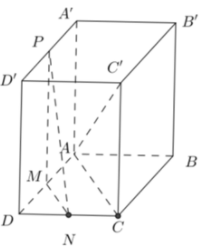
Ta có: //
Có thể bạn quan tâm
- Trắc nghiệm Khoảng cách (có đáp án) (1075 lượt thi)
- Khoảng cách có đáp án (425 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Nhận biết) (424 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Thông hiểu) (377 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (481 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1381 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (1071 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (867 lượt thi)
- Trắc nghiệm Vectơ trong không gian (có đáp án) (737 lượt thi)
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (725 lượt thi)
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (588 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (580 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (573 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (508 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Thông hiểu) (452 lượt thi)
