Cho tứ diện SABC trong đo SA, SB, SC vuông góc với nhau từng đôi một và $SA=3a$, $SB=a$,$SC=2a$. Khoảng cách từ A đến đường thẳng BC bằng:

Đáp án đúng là : B

Lời giải:

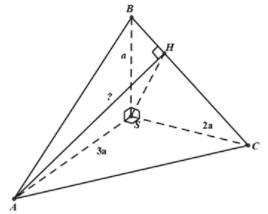
+ Dựng  $AH\perp BC$ $\Rightarrow d\left(A,BC\right)=AH$

+ $\left\{\begin{array}{l}AS\perp \left(SBC\right)\supset BC\Rightarrow AS\perp BC\\ AH\perp BC\end{array}\right.$

AH cắt Á cùng nằm trong $\left(SAH\right)$.

$\Rightarrow BC\perp \left(SAH\right)\supset SH\Rightarrow BC\perp SH$

Xét trong $\Delta SBC$ vuông tại S có H là đường cao ta có:

$\frac{1}{S{H}^2}=\frac{1}{S{B}^2}+\frac{1}{S{C}^2}$

$=\frac{1}{a^2}+\frac{1}{4a^2}=\frac{5}{4a^2}$  

$\Rightarrow S{H}^2=\frac{4a^2}{5}$

$\Rightarrow SH=\frac{2a\sqrt{5}}{5}$

+ Ta dễ chứng minh được  $AS\perp \left(SBC\right)\supset SH\Rightarrow AS\perp SH$ 

$\Rightarrow \Delta ASH$ vuông tại S.

Áp dụng hệ thức lượng trong $\Delta ASH$ vuông tại S ta có:

$A{H}^2=S{A}^2+S{H}^2$

$=9a^2+\frac{4a^2}{5}=\frac{49a^2}{5}$

$\Rightarrow AH=\frac{7a\sqrt{5}}{5}$

*Phương pháp giải:

Sử dụng phương pháp tính khoảng cách từ đường thẳng tới mặt phẳng

*Lý thuyết:

1. Khoảng cách từ một điểm đến một đường thẳng

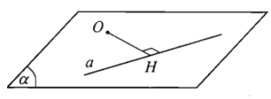
Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.

Kí hiệu: d(O; a).

2. Khoảng cách từ một điểm đến một mặt phẳng

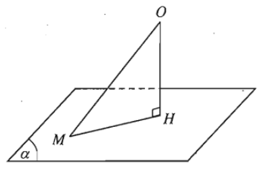
Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).

1. Khoảng cách giữa đường thẳng và măt phẳng song song.

- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).

Kí hiệu là d(a; (α)) .

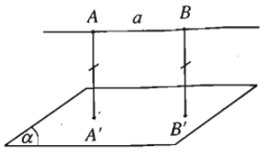
2. Khoảng cách giữa hai mặt phẳng song song.

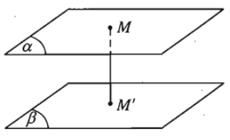
- Định nghĩa: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

- Kí hiệu: d((α); (β)).

Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).

Xem thêm

Lý thuyết Khoảng cách (mới  + Bài Tập) - Toán 11 

TOP 40 câu Trắc nghiệm Khoảng cách (có đáp án ) – Toán 11