Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai cạnh đối AB và CD bằng

Đáp án đúng là: A

Lời  giải:

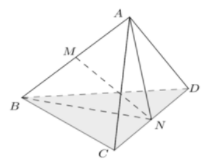
Gọi M, N lần lượt là trung điểm của AB và CD.

Khi đó $NA=NB=\frac{a\sqrt{3}}{2}$ nên tam giác ANB cân, suy ra $NM\perp AB$.

Chứng minh tương tự ta có $NM\perp DC$, nên $d\left(AB;CD\right)=MN$.

Ta có:

$S_{ABN}$$=\sqrt{p\left(p-AB\right)\left(p-BN\right)\left(p-AN\right)}$ (p là nửa chu vi)

$=\sqrt{\frac{a+a\sqrt{3}}{2}.\frac{a+a\sqrt{3}}{2}.\frac{a}{2}.\frac{a}{2}}$

$=\frac{\sqrt{2}a}{4}$

Mặt khác:  

$S_{ABN}=\frac{1}{2}AB.MN=\frac{1}{2}a.MN$

$\Rightarrow MN=\frac{\sqrt{2}a}{2}$

*Phương pháp giải:

1.Gọi M,I lần lượt là trung điểm là CD và AB.Chứng minhd(AB,CD)=MI

2.Tính MI

*Lý thuyết:

Trong không gian tọa đọ Oxyz, có 4 vị trí tương đối của 2 đường thẳng đó là trùng nhau, cắt nhau, chéo nhau và song song. Trong trường hợp 2 đường thẳng chéo nhau, khoảng cách giữa chúng là độ dài đoạn vuông góc chung của 2 đường thẳng. Trong đó, đoạn thẳng nối 2 điểm trên 2 đường thẳng chéo nhau, đồng thời vuông góc với cả 2 đường thẳng đó chính là đoạn vuông góc chung.

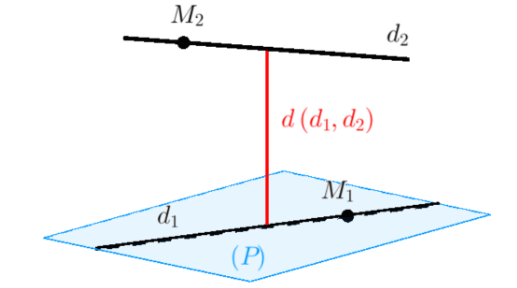
Lưu ý, đoạn vuông góc chung của 2 đường thẳng chéo nhau là chỉ có một và tồn tại duy nhất.

2. Phương pháp tính khoảng cách giữa 2 đường thẳng chéo nhau

Để có thể tính được khoảng cách giữa 2 đường thẳng chéo nhau thì chúng ta có thể sử dụng một trong các cách dưới đây:

Phương pháp 1: Dựng đoạn vuông góc chung MN của a và b, khi đó d (a,b) = MN.

Tuy nhiên, khi dựng đoạn vuông góc chung MN, chúng ta có thể sẽ gặp phải các trường hợp sau:

- Trường hợp 1: ∆ và ∆’ vừa chéo vừa vuông góc với nhau

Khi gặp trường hợp này, chúng ta sẽ làm như sau:

• Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
• Bước 2: Trong mặt phẳng (α) kẻ đường thẳng IJ vuông góc với ∆’

Khi đó IJ chính là đoạn vuông góc chung và d (∆, ∆’) = IJ.

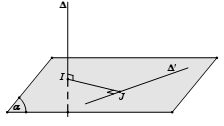
- Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau

• Bước 1: Bạn chọn một mặt phẳng (α) chứa ∆’ và song song với ∆
• Bước 2: Bạn dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M thuộc ∆ dựng đoạn MN vuông góc với (α) . Khi đó, d  sẽ là đường thẳng đi qua N và song song với ∆
• Bước 3: Bạn gọi H là giao điểm của đường thẳng d với ∆’, dựng HK // MN

Khi đó, HK chính là đoạn vuông góc chung và d (∆, ∆’) = HK = MN.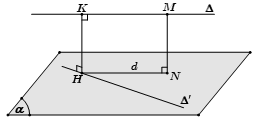

Hoặc bạn làm như sau:

• Bước 1: Chọn mặt phẳng (α) vuông góc với ∆ tại I
• Bước 2: Bạn tìm hình chiếu d của ∆’ xuống mặt phẳng (α)
• Bước 3: Trong mặt phẳng (α), dựng IJ vuông góc với d, từ J bạn dựng đường thẳng song song với ∆ và cắt ∆’ tại H, từ H dựng HM // IJ

Khi đó, HM chính là đoạn vuông góc chung và d (∆, ∆’) = HM = IJ.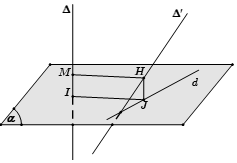

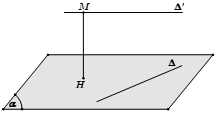
Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó, d (∆, ∆’) = d (∆’, (α)).

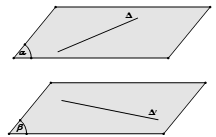
Phương pháp 3: Dựng 2 mặt phẳng song song và lần lượt chứa 2 đường thẳng. Khoảng cách giữa 2 mặt phẳng đó chính là khoảng cách giữa 2 đường thẳng cần tìm.

Lưu ý: Phương pháp này thường sử dụng trong trường hợp khi kẻ đường thẳng song song với 1 trong 2 đường đề bài cho ban đầu gặp khó khăn.

Phương pháp 4: Sử dụng phương pháp vec tơ

* MN là đoạn vuông góc chung của AB và CD khi và chỉ khi:

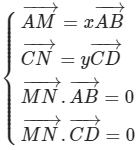
* Nếu trong mặt phẳng (α) có hai véc tơ không cùng phương thì:

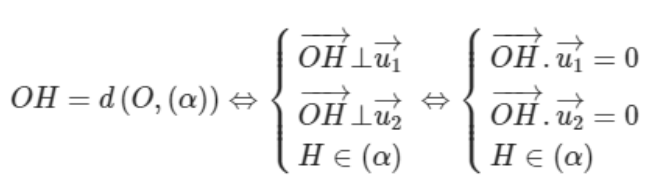
Xem thêm

Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập 

TOP 20 câu Trắc nghiệm Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách (Kết nối tri thức 2024) có đáp án - Toán 10