Trắc nghiệm Vectơ trong không gian (có đáp án)
Trắc nghiệm Toán 11 Bài 1: Vectơ trong không gian
-
714 lượt thi
-
27 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
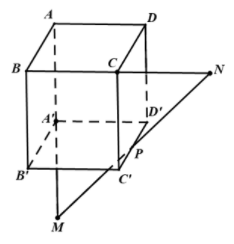
Đặt .
Vì nên
,
Ta có
Do
.
Vậy .
Câu 2:
18/07/2024Giả sử là ba điểm lần lượt nằm trên ba cạnh cỏ tứ diện SABC. Gọi I là giao điểm của ba mặt phẳng và J là giao điểm của ba mặt phẳng .
Ta được thẳng hàng tính đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
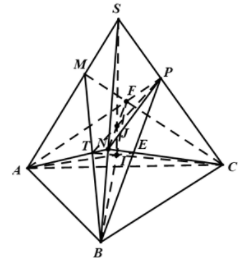
Goi .
Trong có trong có .
Đặt
và
Ta có
Do nên
Vì không cùng phương nên ta có
Hoàn toàn tương tự ta có :
Làm tương tự như trên đối với hai giao điểm và ta được :
Suy ra
Vậy thẳng hàng và
Câu 3:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
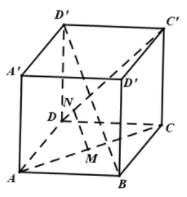
Giả sử
Dễ dàng có các biểu diễn
và .
Từ đó suy ra
Để thì
Từ và ta có:
Vậy các điểm được xác định bởi
Ta cũng có
Câu 4:
22/07/2024Cho tứ diện ABCD. Lấy các điểm M, N, P, Q lần lượt thuộc AB, BC, CD, DA sao cho
.
Hãy xác định k để M, N, P, Q đồng phẳng.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
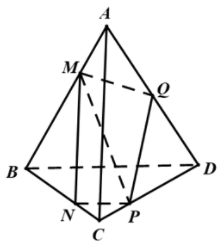
Cách 1.
Ta có
Lại có do đó
Vậy Nếu đồng phẳng thì
hay
.
Cách 2. Đặt thì không khó khăn ta có các biểu diễn
, ,
Các điểm đồng phẳng khi và chỉ khi các vec tơ đồng phẳng
Do các vec tơ không đồng phẳng nên điều này tương đương với
Câu 5:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải: :
Do đúng với mọi điểm nên câu B sai.
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải: :
Ba véctơ đồng phẳng khi và chỉ khi ba véctơ đó có giá song song hoặc thuộc một mặt phẳng. Câu A sai
Câu 7:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
Ta chứng minh được nên
Câu 8:
23/07/2024Cho ba vectơ . Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải: :
Câu D sai. Ví dụ phản chứng 3 cạnh của hình chóp tam giác đồng qui tại 1 đỉnh nhưng chúng không đồng phẳng.
Câu 9:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
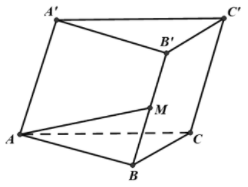
Ta có
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
Ta có:
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Vì I là trọng tâm tam giác ABC nên
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Câu A sai vì ba véctơ đồng phẳng là ba véctơ có giá cùng song song với cùng một mặt phẳng.
Câu B sai vì thiếu điều kiện 2 véctơ không cùng phương.
Câu C sai vì với là véctơ bất kì không phải là điều kiện để 3 véctơ đồng phẳng.
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Với ta có:
Câu 14:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Nếu thì nên .
Suy ra đi qua trọng tâm của tam giấc ABC
=> là đáp án đúng.
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Gọi O là tâm hình bình hành ABCD. Ta có:
=>
Câu 16:
26/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Lời giải:
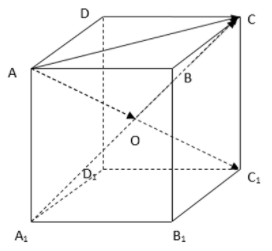
+ Gọi O là tâm của hình hộp .
+ Vận dụng công thức trung điểm để kiểm tra.
*Phương pháp giải:
Vận dụng công thức trung điểm
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
( M tùy ý )
*Lý thuyết:
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
( M tùy ý )
- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:
( M tùy ý )
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì .
Xem thêm
Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto (2024) chi tiết nhấtCâu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:

là hình bình hành
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
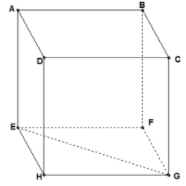
(Vì ).
Câu 19:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:

Câu 20:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
A. Đúng vì cùng thuộc
B. Đúng vì
C. Sai vì
ba véctơ đồng phẳng.
D. Đúng vì theo câu C
Câu 21:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
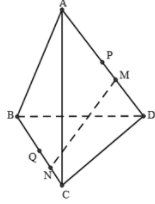
A. Sai vì
không đồng phẳng.
B. Đúng vì
: đồng phẳng.
C. Đúng. Bằng cách biểu diễn tương tự như trên ta có
D. Đúng. Biểu diễn giống đáp án A ta có .
Câu 22:
12/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
* Phương pháp giải:
Sử dụng định ngĩa vectơ, phép cộng và phép trừ vec tơ trong không gian, điều kiện đồng phẳng của ba vectơ để tìm mệnh đề sai.
* Lời giải:
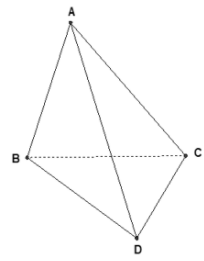
Vì ABCD là tứ diện đều nên các tam giác ABC, BCD, CDA, ABD là các tam giác đều.
A. Đúng vì
B. Đúng vì
C. Sai vì
D. Đúng vì
* Một số dạng bài tập liên quan:
Vectơ và các phép toán vectơ trong không gian.
+ Dạng 1. Chứng minh một đẳng thức vectơ.
+ Dạng 2. Phân tích một vectơ theo các vectơ thành phần.
+ Dạng 3. Góc giữa hai vectơ. Tích vô hướng giữa hai vectơ.
+ Dạng 4. Một số bài toán ứng dụng vectơ giải toán thực tiễn.
Xem thêm các bài viết liên quan hay, chi tiết:
50 Bài tập Vectơ trong không gian Toán 11 mới nhất
Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu)
100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1)
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
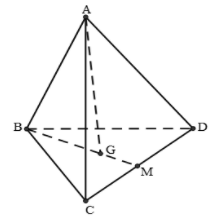
Gọi M là trung điểm BC.
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
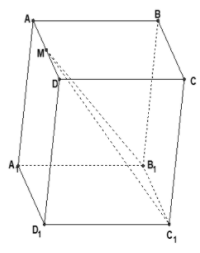
A. Sai vì
B. Đúng vì
C. Sai. theo câu B suy ra
D. Đúng vì
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
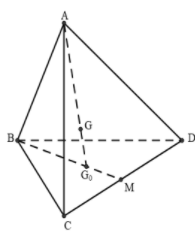
Theo đề: là giao điểm của GA và mp
là trọng tâm tam giác BCD.
Ta có:
Câu 26:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
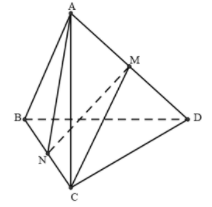
A. Đúng vì
B. Đúng vì từ N ta dựng véctơ bằng véctơ thì không nằm trong mặt phẳng .
C. Sai. Tương tự đáp án B thì không nằm trong mặt phẳng .
D. Đúng vì
Câu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
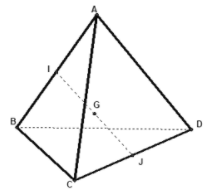
Ta có:
G là trung điểm IJ nên đáp án A đúng
Tương tự cho đáp án B và C cũng đúng.
Có thể bạn quan tâm
- Trắc nghiệm Vectơ trong không gian (có đáp án) (713 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (302 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Nhận biết) (345 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu) (549 lượt thi)
- Trắc nghiệm Vectơ trong không gian có đáp án (Vận dụng) (339 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (1324 lượt thi)
- 100 câu trắc nghiệm Vecto trong không gian nâng cao (phần 1) (1027 lượt thi)
- Trắc nghiệm Khoảng cách (có đáp án) (1017 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng (có đáp án) (843 lượt thi)
- Trắc nghiệm Hai đường thẳng vuông góc (có đáp án) (707 lượt thi)
- Trắc nghiệm Ôn tập chương 3 - Hình Học (có đáp án) (564 lượt thi)
- Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án) (563 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Nhận biết) (491 lượt thi)
- Trắc nghiệm Khoảng cách có đáp án (Vận dụng) (460 lượt thi)
- Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án (Thông hiểu) (431 lượt thi)
