Câu hỏi:
20/07/2024 995
Cho hình chóp S.ABC có cạnh SA⊥(ABC) và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây sai?
A. CH⊥HK
B. AB⊥(CHK)
C. CH⊥AK
D. BC⊥(SAC)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: D
Giải thích:
Đáp án:
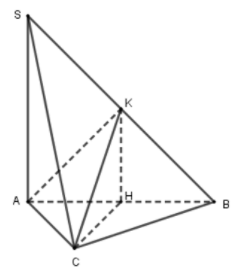
Do ΔABC cân tại C nên CH⊥AB.
Mà SA⊥(ABC) ⇒ SA⊥CH.
Do đó CH⊥(SAB) ⇒ CH⊥HK, CH⊥AK hay A, C đúng.
Ngoài ra HK//SA,SA⊥AB ⇒ HK⊥AB, mà AB⊥CH ⇒AB⊥(CHK) hay B đúng.
D sai vì BC không vuông góc với AC nên không có BC⊥(SAC).
Đáp án: D
Giải thích:
Đáp án:

Do ΔABC cân tại C nên CH⊥AB.
Mà SA⊥(ABC) ⇒ SA⊥CH.
Do đó CH⊥(SAB) ⇒ CH⊥HK, CH⊥AK hay A, C đúng.
Ngoài ra HK//SA,SA⊥AB ⇒ HK⊥AB, mà AB⊥CH ⇒AB⊥(CHK) hay B đúng.
D sai vì BC không vuông góc với AC nên không có BC⊥(SAC).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a;AD=2a(a>0). Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy .Biết mặt phẳng (SAC) hợp với (ABCD) một góc 60o . tính khoảng cách giữa CD và SB.
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?
Câu 3:
Cho ba vectơ →a,→b,→c không đồng phẳng xét các vectơ
→x=2→a−→b;→y=−4→a+2→b; →z=−3→a−2→c
Chọn mệnh đề đúng trong các mệnh đề sau:
Cho ba vectơ →a,→b,→c không đồng phẳng xét các vectơ
→x=2→a−→b;→y=−4→a+2→b; →z=−3→a−2→c
Chọn mệnh đề đúng trong các mệnh đề sau:
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I): AI⊥SC
(II): (SBC)⊥(SAC)
(III): AI⊥BC
(IV): (ABI)⊥(SBC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I): AI⊥SC
(II): (SBC)⊥(SAC)
(III): AI⊥BC
(IV): (ABI)⊥(SBC)


