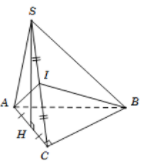
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(I): AI⊥SC

(II): (SBC)⊥(SAC)

(III): AI⊥BC

(IV): (ABI)⊥(SBC)

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và $SA =a\sqrt{15}$ Gọi M, N lần lượt là trung điểm của BC và CD:

a) Chứng minh (SAC) ⊥ (SBD).

b) Tính góc giữa SM và (ABCD).

c) Tính khoảng cách từ điểm C đến mặt phẳng (SMN)?

Trên đồ thị của hàm số $y = \frac{1}{x-1}$ có điểm M sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2. Tìm tọa độ M?

Tìm m để các hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2+mx+2m+1}{x+1} khi x\ge 0\\ \frac{2x+3m-1}{\sqrt{1-x}+2} khi x<0\end{array}\right.$ có giới hạn khi x → 1.

Chứng minh phương trình sau luôn luôn có nghiệm: $(m^2-2m+2)x^3+3x-3=0$

Tính giới hạn sau: $\underset{x\to -2^{+}}{\lim }\frac{x}{x^2+5x+6}$

Tính giới hạn sau: $\underset{x\to -\infty }{\lim }\frac{\sqrt{9x^2+1}-4x}{3-2x}$

Phần II: Tự luận

Tính giới hạn sau: $C=lim\frac{3.2^n-3^n}{2^{n+1}+3^{n+1}}$

Cho hàm số $y=k{x}^3+\sqrt{x^2+x-2}.$ Với giá trị nào của k thì $y\text{'}\left(2\right)=\frac{53}{4}$?

Tìm m để hàm số sau có giới hạn khi x → 1.

$f\left(x\right)=\left\{\begin{array}{l}\frac{x^2+x-2}{\sqrt{1-x}}+mx+1 khi x<1\\ 3mx+2m-1 khi x\ge 1\end{array}\right.$

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và(ABC).