15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Thông hiểu)

Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Thông hiểu)

Đề số 1

Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Thông hiểu)

291 lượt thi
15 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(I): AI $⊥$ SC

(II): (SBC) $⊥$ (SAC)

(III): AI $⊥$ BC

(IV): (ABI) $⊥$ (SBC)

A. 1

B. 2

C. 3

D. 4

Đáp án D

Tam giác SAC đều có I là trung điểm của SC nên AI $⊥$ SC.

⇒ Mệnh đề (I) đúng.

Gọi H là trung điểm AC suy ra SH $⊥$ AC. $⊥$

Mà (SAC) $⊥$ (ABC) theo giao tuyến AC nên SH $⊥$ (ABC) do đó SH $⊥$ BC.

Hơn nữa theo giả thiết tam giác ABC vuông tại C nên BCAC.

Từ đó suy ra BC $⊥$ (SAC) ⇒ BC $⊥$ AI. Do đó mệnh đề (III) đúng.

Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.

Ta có: $\{\begin{matrix} BC ⊥ AC \\ BC ⊥ SH \end{matrix}$ ⇒ BC $⊥$ (SAC)

BC $\subset$ (SBC) ⇒ (SBC) $⊥$ (SAC)

Vậy mệnh đề (II) đúng.

Câu 2:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?

A. BC $⊥$ AH.

B. (AHK) $⊥$ (SBC).

C. SC $⊥$ AI.

D. Tam giác IAC đều.

Đáp án D

Dùng phương pháp loại trừ thì D là đáp án sai.

Câu 3:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = $a \sqrt{3}$ và vuông góc với mặt đáy (ABC). Gọi $φ$ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?

A. $φ = 30^{0}$

B. $sinφ = \frac{\sqrt{5}}{5}$

C. $φ = 60^{0}$

D. $sinφ = \frac{2 \sqrt{5}}{5}$

Đáp án D

Gọi M là trung điểm của BC, suy ra AM $⊥$ BC.

Câu 4:

Cho tứ diện S.ABC có các cạnh SA, SB; SC đôi một vuông góc và SA = SB = SC = 1. Tính cos $α$ , trong đó $α$ là góc giữa hai mặt phẳng (SBC) và (ABC) ?

A. $cosα = \frac{1}{\sqrt{2}}$

B. $cosα = \frac{1}{2 \sqrt{3}}$

C. $cosα = \frac{1}{3 \sqrt{2}}$

D. $cosα = \frac{1}{\sqrt{3}}$

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a. Cạnh bên SA = a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng $45^{0}$ . Độ dài AC bằng

A. $a \sqrt{2}$

B. $a \sqrt{3}$

C. 2a

D. a

Đáp án A

Câu 6:

Cho tam giác đều ABC cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại D lấy điểm S sao cho SD = $\frac{a \sqrt{6}}{2}$ . Gọi I là trung điểm BC; kẻ IH vuông góc SA (H thuộc SA). Khẳng định nào sau đây sai?

A. SA $⊥$ BH

B. (SDB) $⊥$ (SDC).

C. (SAB) $⊥$ (SAC).

D. BH $⊥$ HC.

Đáp án B

Dùng phương pháp loại trừ thì B là đáp án sai.

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = $\frac{a \sqrt{3}}{2}$ . Tính góc giữa hai mặt phẳng (SBC) và (ABCD).

A. $30^{0}$

B. $45^{0}$

C. $60^{0}$

D. $90^{0}$

Đáp án C

Gọi Q là trung điểm BC, suy ra OQ $⊥$ BC

Câu 8:

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.

A. $\frac{1}{2}$

B. $\frac{1}{\sqrt{3}}$

C. $\frac{1}{3}$

D. $\frac{1}{\sqrt{2}}$

Đáp án B

Gọi O là trung điểm của AC. Vì S.ABCD là hình chóp đều nên SO $⊥$ (ABCD).

Gọi H là trung điểm của BC và góc giữa mặt bên (SBC) và mặt đáy (ABCD) là $α$ .

Ta có (SBC) $\cap$ (ABCD) = BC mà BC $⊥$ SH và BC $⊥$ OH nên $\hat{SHO} = α$

SH là đường cao của tam giác đều SBC cạnh a nên SH = $\frac{a \sqrt{3}}{2}$

Xét tam giác SOH vuông tại O có: cos $α$ = $\frac{OH}{SH} = \frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}} = \frac{1}{\sqrt{3}}$

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, đường thẳng SO vuông góc với mặt phẳng (ABCD). Biết BC = SB = a, SO = $\frac{a \sqrt{6}}{3}$ . Tìm số đo của góc giữa hai mặt phẳng (SBC)và (SCD).

A. $90^{0}$

B. $60^{0}$

C. $45^{0}$

D. $30^{0}$

Đáp án A

Gọi M là trung điểm của SC, do tam giác SBC cân tại B nên ta có SC $⊥$ BM (1).

Theo giả thiết ta có BD $⊥$ (SAC) ⇒ SC $⊥$ BD. Do đó SC $⊥$ (BCM) suy ra SC $⊥$ DM (2).

Từ (1) và (2) suy ra góc giữa hai mặt phẳng (SBC) và (SCD) là góc giữa hai đường thẳng BM và DM.

Ta có $∆$ SBO = $∆$ CBO suy ra SO = CO = $\frac{a \sqrt{6}}{3}$

Do đó OM = $\frac{1}{2} SC = \frac{a \sqrt{3}}{3}$

Mặt khác OB = $\sqrt{{SB}^{2} - {SO}^{2}} = \frac{a \sqrt{3}}{3}$ . Do đó tam giác BMO vuông cân tại M hay góc $\hat{BMO} = 45^{0}$ hay $\hat{BMD} = 90^{0}$

Vậy góc giữa hai mặt phẳng (SBC) và (SCD) là $90^{0}$

Câu 10:

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, cạnh bên SA vuông góc với mặt phẳng đáy, AB = BC = a và SA = a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng

A. $60^{0}$

B. $90^{0}$

C. $30^{0}$

D. $45^{0}$

Đáp án đúng: A

*Lời giải:

Gọi H là trung điểm cạnh AC

Ta có (SAC) $⊥$ (ABC) (vì SA $⊥$ (ABC)) và BH $⊥$ AC ⇒ BH $⊥$ (SAC)

Trong mặt phẳng (SAC), kẻ HK $⊥$ SC thì SC $⊥$ (BHK) ⇒ SC $⊥$ BK

⇒ $(\hat{SAC); (SBC}) = (\hat{SKH}) = φ$

Mặt khác

Tam giác ABC vuông cân tại B có AB = BC = a nên AC = $a \sqrt{2}$ và BH = $\frac{a \sqrt{2}}{2}$

Hai tam giác CKH và CAS đồng dạng nên HK = $\frac{HC . SA}{SC}$ $\Leftrightarrow \frac{HC . SA}{\sqrt{{SA}^{2} + {AC}^{2}}} = \frac{a \sqrt{2}}{\sqrt{3}}$

Tam giác BHK vuông tại H có tan $φ$ = $\frac{BH}{BK} = \sqrt{3} \Rightarrow φ = 60^{0}$

Vậy $(\hat{SAC); (SBC}) = 60^{0}$

*Phương pháp giải

Áp dụng lý thuyết về hai mặt phẳng vuông góc với nhau để làm

*Lý thuyến cần nắm và dạng toán về hai mặt phẳng vuông góc:

1. Góc giữa hai mặt phẳng

Góc giữa hai mặt phẳng $(α)$ và $(β)$ là góc giữa hai đường thẳng lần lượt vuông góc với $(α)$ và $(β)$ , kí hiệu $((α), (β))$ .

Ta có: $((α), (β)) = (m, n)$ với $m ⊥ (α), n ⊥ (β)$ .

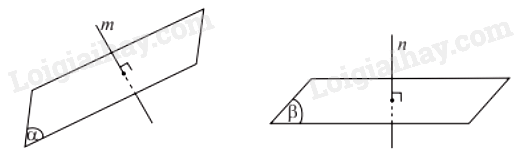
2. Hai mặt phẳng vuông góc

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là một góc vuông.

Hai mặt phẳng (P) và (Q) vuông góc được kí hiệu là $(P) ⊥ (Q)$ .

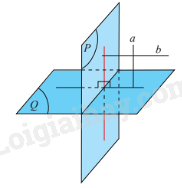
3. Điều kiện để hai mặt phẳng vuông góc

Định lí 1:

Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

4. Tính chất cơ bản về hai mặt phẳng vuông góc

Định lí 2:

Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

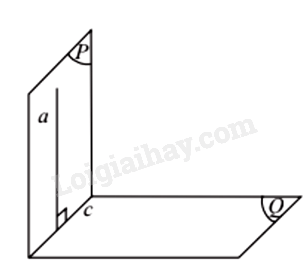
Định lí 3:

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

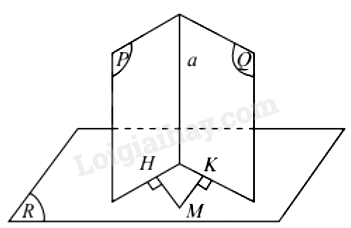
5. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

Hình lăng trụ đều là hình lăng trụ đúng có mặt đáy là đa giác đều.

Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.

Hình hộp chữ nhật là hình hộp đứng có mặt đáy là hình chữ nhật.

Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Hai mặt phẳng vuông góc – Toán 11 Chân trời sáng tạo

Chuyên đề Hai mặt phẳng vuông góc (2024) - Toán 11

Câu 11:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, các cạnh SA = SB = a, SD = $a \sqrt{2}$ . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng $90^{0}$ . Độ dài đoạn thẳng BD

A. 2a

B. 2a $\sqrt{3}$

C. a $\sqrt{3}$

D. a $\sqrt{2}$

Đáp án C

Gọi I là tâm của hình thoi ABCD.

Và H là hình chiếu vuông góc của S lên BD.

Câu 12:

Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Cạnh bên SA vuông góc với đáy (ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD).

A. $\frac{1}{\sqrt{5}}$

B. $\frac{2}{\sqrt{5}}$

C. $\sqrt{5}$

D. $\frac{\sqrt{5}}{2}$

Đáp án C

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc $\hat{BAD} = 60^{0}$ , SA = SB = SD = $\frac{a \sqrt{3}}{2}$ . Gọi $φ$ là góc giữa hai mặt phẳng(SBD) và (ABCD). Mệnh đề nào sau đây đúng?

A. $tanφ = \sqrt{5}$

B. $tanφ = \frac{\sqrt{5}}{5}$

C. $tanφ = \frac{\sqrt{3}}{2}$

D. $φ = 45^{0}$

Đáp án A

Từ giả thiết suy ra tam giác ABD đều cạnh a.

Gọi H là hình chiếu của S trên mặt phẳng (ABCD).

Do SA = SB = SD nên suy ra H là tâm của tam gác đều ABD.

Câu 14:

Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh $a \sqrt{2}$ , biết các cạnh bên tạo với đáy một góc $60^{0}$ . Giá trị lượng giác tang của góc giữa hai mặt phẳng (SAC) và (SCD) bằng

A. $\frac{2 \sqrt{3}}{3}$

B. $\frac{\sqrt{21}}{3}$

C. $\frac{\sqrt{21}}{7}$

D. $\frac{\sqrt{3}}{2}$

Đáp án A

Kẻ OK $⊥$ SC.

Do S.ABCD là hình chóp đều và ABCD là hình vuông nên SO $⊥$ (ABCD); BD $⊥$ (SAC) ⇒ SC $⊥$ BD Suy ra SC

$⊥$ (BKD) ⇒ KD $⊥$ SC

Vậy góc giữa hai mặt phẳng (SAC) và (SCD) là $\hat{OKD}$ và $\tan \hat{OKD} = \frac{OD}{OK}$ (do $Δ$ KOD vuông ở O): ABCD là hình vuông cạnh $a \sqrt{2}$ nên AC = 2a ⇒ OA = OC = OD = a

Trong hình chóp đều S.ABCD, cạnh bên tạo với đáy một góc $60^{0}$ nên

Câu 15:

Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng (ABC), biết AB = AC = a, BC = $a \sqrt{3}$ . Tính góc giữa hai mặt phẳng (SAB) và (SAC).

A. $30^{0}$

B. $150^{0}$

C. $60^{0}$

D. $120^{0}$

(vì góc giữa hai đường thẳng không thể lớn hơn $90^{0}$ ).

Vậy góc giữa hai mặt phẳng (SAB) và (SAC) là $60^{0}$

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương