Câu hỏi:
01/01/2025 1,275Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, cạnh bên SA vuông góc với mặt phẳng đáy, AB = BC = a và SA = a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
Gọi H là trung điểm cạnh AC
Ta có (SAC)(ABC) (vì SA(ABC)) và BHAC ⇒ BH(SAC)
Trong mặt phẳng (SAC), kẻ HKSC thì SC(BHK) ⇒ SCBK
⇒
Mặt khác
Tam giác ABC vuông cân tại B có AB = BC = a nên AC = và BH =
Hai tam giác CKH và CAS đồng dạng nên HK =
Tam giác BHK vuông tại H có tan =
Vậy
*Phương pháp giải
Áp dụng lý thuyết về hai mặt phẳng vuông góc với nhau để làm
*Lý thuyến cần nắm và dạng toán về hai mặt phẳng vuông góc:
1. Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng và là góc giữa hai đường thẳng lần lượt vuông góc với và , kí hiệu .
Ta có: với .
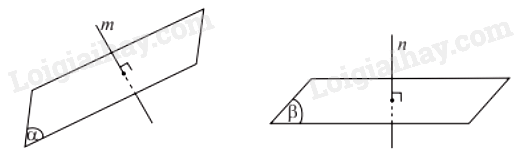
2. Hai mặt phẳng vuông góc
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là một góc vuông.
Hai mặt phẳng (P) và (Q) vuông góc được kí hiệu là .
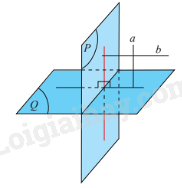
3. Điều kiện để hai mặt phẳng vuông góc
Định lí 1:
Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
4. Tính chất cơ bản về hai mặt phẳng vuông góc
Định lí 2:
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
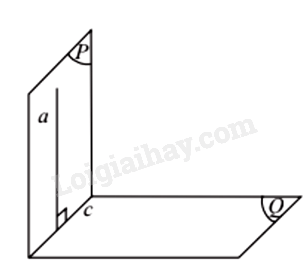
Định lí 3:
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
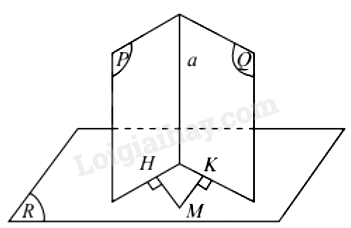
5. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương
Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Hình lăng trụ đều là hình lăng trụ đúng có mặt đáy là đa giác đều.
Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.
Hình hộp chữ nhật là hình hộp đứng có mặt đáy là hình chữ nhật.
Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hai mặt phẳng vuông góc – Toán 11 Chân trời sáng tạo
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác đều ABC cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại D lấy điểm S sao cho SD = . Gọi I là trung điểm BC; kẻ IH vuông góc SA (H thuộc SA). Khẳng định nào sau đây sai?
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, đường thẳng SO vuông góc với mặt phẳng (ABCD). Biết BC = SB = a, SO = . Tìm số đo của góc giữa hai mặt phẳng (SBC)và (SCD).
Câu 3:
Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Cạnh bên SA vuông góc với đáy (ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD).
Câu 4:
Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng (ABC), biết AB = AC = a, BC = . Tính góc giữa hai mặt phẳng (SAB) và (SAC).
Câu 5:
Cho tứ diện S.ABC có các cạnh SA, SB; SC đôi một vuông góc và SA = SB = SC = 1. Tính cos, trong đó là góc giữa hai mặt phẳng (SBC) và (ABC) ?
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = . Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
Câu 7:
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh , biết các cạnh bên tạo với đáy một góc . Giá trị lượng giác tang của góc giữa hai mặt phẳng (SAC) và (SCD) bằng
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, các cạnh SA = SB = a, SD = . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng . Độ dài đoạn thẳng BD
Câu 10:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I): AISC
(II): (SBC)(SAC)
(III): AIBC
(IV): (ABI)(SBC)
Câu 11:
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc , SA = SB = SD = . Gọi là góc giữa hai mặt phẳng(SBD) và (ABCD). Mệnh đề nào sau đây đúng?
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = và vuông góc với mặt đáy (ABC). Gọi là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
Câu 14:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a. Cạnh bên SA = a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng . Độ dài AC bằng


