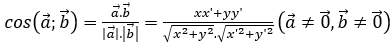Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được

$\left\{\begin{array}{l}\cos {45}^0=\frac{\sqrt{2}}{2}\\ \sin {45}^0=\frac{\sqrt{2}}{2}\end{array}\right.\Rightarrow \cos {45}^0+\sin {45}^0=\sqrt{2}.$ 

Chọn B.

Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được

$\left\{\begin{array}{l}\tan {30}^0=\frac{1}{\sqrt{3}}\\ \cot {30}^0=\sqrt{3}\end{array}\right.\Rightarrow \tan {30}^0+\cot {30}^0=\frac{4}{\sqrt{3}}.$ 

Chọn A.

Ta có $\tan {150}^{\text{O}}=-\tan {30}^0=-\frac{1}{\sqrt{3}}.$ 

Chọn C.

Vì 30⁰ và 60⁰ là hai góc phụ nhau nên $\left\{\begin{array}{l}\sin {30}^0=\cos {60}^0\\ \sin {60}^0=\cos {30}^0\end{array}\right.$

$\Rightarrow P=\cos {30}^{\circ }\cos {60}^{\circ }-\sin {30}^{\circ }\sin {60}^{\circ }=\cos {30}^{\circ }\cos {60}^{\circ }-\cos {60}^{\circ }\cos {30}^{\circ }=0.$ 

Chọn D.

Vì 30⁰ và 60⁰ là hai góc phụ nhau nên $\left\{\begin{array}{l}\sin {30}^0=\cos {60}^0\\ \sin {60}^0=\cos {30}^0\end{array}\right.$

$\Rightarrow P=\sin {30}^{\circ }\cos {60}^{\circ }+\sin {60}^{\circ }\cos {30}^{\circ }={\cos }^2{60}^{\circ }+{\sin }^2{60}^{\circ }=1.$

 Chọn A.

Xét phương án D ta có: 

$\left\{\begin{array}{l}\cos {30}^0=\frac{\sqrt{3}}{2}\\ \sin {120}^0=\sin {60}^0=\frac{\sqrt{3}}{2}\end{array}\right.\Rightarrow \cos {30}^0+\sin {120}^0=\sqrt{3}.$ 

Chọn D

Ta có: $\left\{\begin{array}{l}\cos 0^0=1\\ \sin 0^0=0\end{array}\right.\Rightarrow \cos 0^0+\sin 0^0=1.$ 

Chọn A.

*  $\cos {45}^{\text{O}}=\sin {45}^{\text{O}}.$  ( hai góc phụ nhau thì sin góc này bằng cos góc kia)

* Ta có: $\sin {135}^{\text{O}}=\sin {45}^0$mà $\cos {45}^{\text{O}}=\sin {45}^{\text{O}}.$

Suy ra:  $\cos {45}^{\text{O}}=\sin {135}^{\text{O}}.$

* $\sin {120}^{\text{O}}=\sin {60}^0=c{\text{os30}}^0$           

   *  $\left\{\begin{array}{l}\cos {120}^0=-c{\text{os60}}^0=-\frac{1}{2}\\ \sin {60}^0=\frac{\sqrt{3}}{2}\end{array}\right..$ 

Chọn D.

Ta có; ${\text{cosB =cos 30}}^0=\frac{\sqrt{3}}{2}\Rightarrow \sin C\text{}=c\text{osB = }\frac{\sqrt{3}}{2}$

Và ${\text{sinB =sin 30}}^0=\frac{1}{2}\Rightarrow c\text{os}C\text{}=\text{sinB = }\frac{1}{2}$

Chọn A.

Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường  phân giác .

Suy ra: $\widehat{BAH}=\frac{1}{2}\widehat{BAC}={30}^0;\widehat{ABC}={60}^0;\widehat{AHC}={90}^0$

Do đó, $\sin \widehat{BAH}=\frac{1}{2};c\text{os}\widehat{BAH}=\frac{\sqrt{3}}{2}$. Do đó A sai; B sai.

Ta có $\widehat{ABC}={60}^0\Rightarrow \sin \widehat{ABC}=\frac{\sqrt{3}}{2}.$ Do đó C đúng.

Chọn C.

Hai góc bù nhau $\alpha$ và ${180}^0-\alpha$ thì cho có giá trị của sin bằng nhau.

Chọn C.

Cho $\alpha$ và  $\beta$ là hai góc khác nhau và bù nhau. Ta có:

*$\sin \alpha =\sin \beta .$                

* $\cos \alpha =-\cos \beta .$

* $\tan \alpha =-\tan \beta .$

* $\cot \alpha =-\cot \beta .$

Chọn D.

Hai góc 30⁰ và 150⁰ bù nhau nên $\sin 30°=\sin 150°$

Hai góc 15⁰ và 165⁰ bù nhau nên $\cos 15°=-\cos 165°$.

Do đó $P=\sin 30°\cos 15°+\sin 150°\cos 165°=\sin 30°.c{\text{os15}}^0+\sin 30°.(-\cos 15°)=0$.

Chọn B.

Hai góc $\alpha$ và  $\beta$  bù nhau nên $\sin \alpha =\sin \beta$; $\cos \alpha =-\cos \beta$.

Do đó $P=\cos \alpha \cos \beta -\sin \beta \sin \alpha =-{\cos }^2\alpha -{\sin }^2\alpha =-\left({\sin }^2\alpha +{\cos }^2\alpha \right)=-1$.

 Chọn C.

Giả sử $\widehat{A}=\alpha ;\widehat{B}+\widehat{C}=\beta$. Biểu thức trở thành $P=\sin \alpha \cos \beta +\cos \alpha \sin \beta$.

Trong tam giác ABC, có $\widehat{A}+\widehat{B}+\widehat{C}=180°\Rightarrow \alpha +\beta =180°$.

Do hai góc $\alpha$ và $\beta$ bù nhau nên $\sin \alpha =\sin \beta$; $\cos \alpha =-\cos \beta$.

Do đó, $P=\sin \alpha \cos \beta +\cos \alpha \sin \beta =-\sin \alpha \cos \alpha +\cos \alpha \sin \alpha =0$.

Chọn A.

Giả sử$\widehat{A}=\alpha ;\widehat{B}+\widehat{C}=\beta$. Biểu thức trở thành $P=\cos \alpha \cos \beta -\sin \alpha \sin \beta$.

Trong tam giác ABC có$\widehat{A}+\widehat{B}+\widehat{C}=180°\Rightarrow \alpha +\beta =180°$.

Do hai góc $\alpha$ và $\beta$ bù nhau nên $\sin \alpha =\sin \beta$; $\cos \alpha =-\cos \beta$.

Do đó $P=\cos \alpha \cos \beta -\sin \alpha \sin \beta =-{\cos }^2\alpha -{\sin }^2\alpha =-\left({\sin }^2\alpha +{\cos }^2\alpha \right)=-1$.

 Chọn C.

Hai góc nhọn $\alpha$ và $\beta$  phụ nhau thì :

 $\sin \alpha =\cos \beta ;cos\alpha =sin\beta ;tan\alpha =cot\beta ;$ $\cot \alpha =tan\beta$.

 Chọn A.

Hai góc 15⁰ và 75⁰ phụ nhau nên sin 75⁰ = cos 15⁰

Hai góc 20⁰ và 110⁰ hơn kém nhau 90⁰ nên cos 110⁰ = - sin 20⁰

Do đó, $S={\sin }^{2}15°+{\cos }^{2}20°+{\sin }^{2}75°+{\cos }^{2}110°$

$\begin{array}{l}=\text{}{\sin }^{2}15°+{\cos }^{2}20+{\cos }^{2}15°+{\left(-\sin 20°\right)}^2\text{}\\ =\text{}\left({\sin }^{2}15°+{\cos }^{2}15°\right)+\left({\sin }^{2}20°+{\cos }^{2}20°\right)\text{}=2\end{array}$

ĐÁP ÁN C

Hai góc $\alpha$ và $\beta$ phụ nhau nên $\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta$.

Do đó, $P=\sin \alpha \cos \beta +\sin \beta \cos \alpha ={\sin }^2\alpha +{\cos }^2\alpha =1$.

 Chọn B.

Hai góc$\alpha$và $\beta$ phụ nhau nên $\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta$.

Do đó, $P=\cos \alpha \cos \beta -\sin \beta \sin \alpha =\cos \alpha \sin \alpha -\cos \alpha \sin \alpha =0$.

 Chọn A.

Khi $\alpha$ là góc tù. Ta có:

*sinα > 0           

*cosα < 0

*tanα < 0           

* cotα < 0

 Chọn C.    

Chọn A.

 Đáp án đúng là: D

*Phương pháp giải: Sử dụng các công thức, giá trị lượng giác của một góc từ 0⁰ đến 180⁰

*Lời giải:

Từ biểu thức ${\cos }^2\alpha +{\sin }^2\alpha =1$ ta suy ra ${\cos }^2\frac{\alpha }{5}+{\sin }^2\frac{\alpha }{5}=1.$

Do đó ta có $5\left({\cos }^2\frac{\alpha }{5}+{\sin }^2\frac{\alpha }{5}\right)=5.$

* Một số lý thuyết liên quan:

Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
 

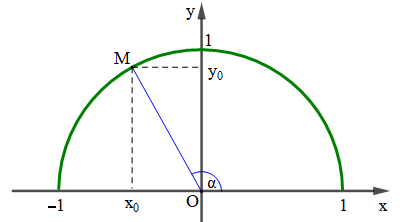
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$ . Gọi ($x_0$; $y_0$) là toạ độ điểm M, ta có:

- Tung độ $y_0$ của M là sin của góc α, kí hiệu là sinα = $y_0$;

- Hoành độ $x_0$ của M là côsin của góc α, kí hiệu là cosα = $x_0$;

- Tỉ số $\frac{y_0}{x_0}$ ($x_0$ ≠ 0) là tang của góc α, kí hiệu là $\tan \alpha =\frac{y_0}{x_0};$  

- Tỉ số  $\frac{y_0}{x_0}$ ($y_0$ ≠ 0) là côtang của góc α, kí hiệu là $\tan \alpha =\frac{x_0}{y_0};$

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:

sin(180° ‒ α) = sinα;

cos(180° ‒ α) = ‒cosα;

tan(180° ‒ α) = ‒tanα (α ≠ 90°);

cot(180° ‒ α) = ‒cotα (0° < α < 180°).

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức

TOP 15 câu Trắc nghiệm Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (Cánh diều 2024) có đáp án - Toán 10

Giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập (2024) chi tiết nhất

Ta có biểu thức ${\sin }^2\frac{\alpha }{3}+{\cos }^2\frac{\alpha }{3}=1\iff {\cos }^2\frac{\alpha }{3}=1-{\sin }^2\frac{\alpha }{3}=\frac{16}{25}.$ 

Do đó ta có $P=3{\sin }^2\frac{\alpha }{3}+5{\cos }^2\frac{\alpha }{3}=3.{\left(\frac{3}{5}\right)}^2+5.\frac{16}{25}=\frac{107}{25}.$

Chọn B

Chia cả tử và mẫu cho cosα ta được:

 $P=\frac{6\sin \alpha -7\cos \alpha }{6\cos \alpha +7\sin \alpha }=\frac{6\frac{\sin \alpha }{\cos \alpha }-7}{6+7\frac{\sin \alpha }{\cos \alpha }}=\frac{6\tan \alpha -7}{6+7\tan \alpha }=\frac{6.(-3)-7}{6+7.(-3)}=\frac{-25}{-15}=\frac{5}{3}.$ 

Chọn B.

Ta có biểu thức ${\sin }^2\alpha +{\cos }^2\alpha =1\iff {\sin }^2\alpha =1-{\cos }^2\alpha =\frac{5}{9}.$ 

Ta có  $P=\frac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }=\frac{\frac{\cos \alpha }{\sin \alpha }+3\frac{\sin \alpha }{\cos \alpha }}{2\frac{\cos \alpha }{\sin \alpha }+\frac{\sin \alpha }{\cos \alpha }}=\frac{{\cos }^2\alpha +3{\sin }^2\alpha }{2{\cos }^2\alpha +{\sin }^2\alpha }=\frac{{\left(-\frac{2}{3}\right)}^2+3.\frac{5}{9}}{2.{\left(-\frac{2}{3}\right)}^2+\frac{5}{9}}=\frac{19}{13}.$

Chọn B.

Ta có

Chọn D.

Ta có $3\cos \alpha -\sin \alpha =1\iff 3\cos \alpha =\sin \alpha +1\to 9{\cos }^2\alpha ={\left(\sin \alpha +1\right)}^2$

$\iff 9{\cos }^2\alpha ={\sin }^2\alpha +2\sin \alpha +1\iff 9\left(1-{\sin }^2\alpha \right)={\sin }^2\alpha +2\sin \alpha +1$ 

$\iff 10{\sin }^2\alpha +2\sin \alpha -8=0\iff \left[\begin{array}{l}\sin \alpha =-1\\ \sin \alpha =\frac{4}{5}\end{array}\right..$

 $\sin \alpha =-1$: không thỏa mãn vì $0^0<\alpha <{90}^0.$

$\sin \alpha =\frac{4}{5}\Rightarrow \cos \alpha =\frac{3}{5}\Rightarrow \tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{4}{3}.$  

Chọn A.

Ta có $2\cos \alpha +\sqrt{2}\sin \alpha =2\iff \sqrt{2}\sin \alpha =2-2\cos \alpha \to 2{\sin }^2\alpha ={\left(2-2\cos \alpha \right)}^2$

$\begin{array}{l}\iff 2{\sin }^2\alpha =4-8\cos \alpha +4{\cos }^2\alpha \iff 2\left(1-{\cos }^2\alpha \right)=4-8\cos \alpha +4{\cos }^2\alpha \\ \iff 6{\cos }^2\alpha -8\cos \alpha +2=0\iff \left[\begin{array}{l}\cos \alpha =1\\ \cos \alpha =\frac{1}{3}\end{array}\right..\end{array}$

 $\cos \alpha =1$: không thỏa mãn vì $0^0<\alpha <{90}^0.$

$\cos \alpha =\frac{1}{3}\Rightarrow \sin \alpha =\frac{2\sqrt{2}}{3}\Rightarrow \cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{\sqrt{2}}{4}.$ 

Chọn C.

Ta có $\sin \alpha +\cos \alpha =a\Rightarrow {\left(\sin \alpha +\cos \alpha \right)}^2=a^2$

$\begin{array}{l}\iff {\sin }^2\alpha +2\sin \alpha \cos \alpha +\text{}c{\text{os}}^2\alpha =a^2\\ \iff 1+2\sin \alpha \cos \alpha =a^2\iff \sin \alpha \cos \alpha =\frac{a^2-1}{2}.\end{array}$

Chọn C.

Ta có $\cos \alpha +\sin \alpha =\frac{1}{3}\Rightarrow {\left(\cos \alpha +\sin \alpha \right)}^2=\frac{1}{9}$

$\iff 1+2\sin \alpha \cos \alpha =\frac{1}{9}\iff \sin \alpha \cos \alpha =-\frac{4}{9}.$

Ta có 

$P=\sqrt{{\tan }^2\alpha +{\cot }^2\alpha }=\sqrt{{\left(\tan \alpha +\cot \alpha \right)}^2-2\tan \alpha \cot \alpha }=\sqrt{{\left(\frac{\sin \alpha }{\cos \alpha }+\frac{\cos \alpha }{\sin \alpha }\right)}^2-2}$

$=\sqrt{{\left(\frac{{\sin }^2\alpha +{\cos }^2\alpha }{\sin \alpha \cos \alpha }\right)}^2-2}=\sqrt{{\left(\frac{1}{\sin \alpha \cos \alpha }\right)}^2-2}=\sqrt{{\left(-\frac{9}{4}\right)}^2-2}=\frac{7}{4}.$ 

Chọn B.

Đáp án đúng là B.

Lời giải

Ta có $\sin \alpha -\cos \alpha =\frac{1}{\sqrt{5}}\Rightarrow {\left(\sin \alpha -\cos \alpha \right)}^2=\frac{1}{5}$

$\iff 1-2\sin \alpha \cos \alpha =\frac{1}{5}\iff \sin \alpha \cos \alpha =\frac{2}{5}.$

Ta có $P=\sqrt{{\sin }^4\alpha +{\cos }^4\alpha }=\sqrt{{\left({\sin }^2\alpha +{\cos }^2\alpha \right)}^2-2{\sin }^2\alpha {\cos }^2\alpha }$

$=\sqrt{1-2{\left(\sin \alpha cos\alpha \right)}^2}=\frac{\sqrt{17}}{5}.$ 

*Phương pháp giải

Sử dụng công thức lượng giác cơ bản

Tách thành hằng đẳng thức

*Lý thuyết:

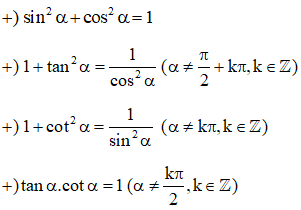
Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới  + Bài Tập) – Toán 11 

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án ) – Toán 11 

Đáp án đúng: A

*Lời giải

Vẽ $\overrightarrow{NE}=\overrightarrow{MN}$.

Khi đó $\left(\overrightarrow{MN},\overrightarrow{NP}\right)=\left(\overrightarrow{NE},\overrightarrow{NP}\right)$

$=\widehat{PNE}={180}^0-\widehat{MNP}={180}^0-{60}^0={120}^0.$ 

 Vẽ $\overrightarrow{OF}=\overrightarrow{MO}$. Khi đó $\left(\overrightarrow{MO},\overrightarrow{ON}\right)=\left(\overrightarrow{OF},\overrightarrow{ON}\right)=\widehat{NOF}={60}^0.$

 Vì $MN\perp OP\Rightarrow \left(\overrightarrow{MN},\overrightarrow{OP}\right)={90}^0.$ 

 Ta có $\left(\overrightarrow{MN},\overrightarrow{MP}\right)=\widehat{NMP}={60}^0.$

*Phương pháp giải

- Ta có tam giác MNP đều nên các góc đều bằng 60 

- vẽ vectơ NE = vectơ MN. khi đó: góc tạo bởi 2 vectơ (MN,NP) = góc tạo bởi 2 vectơ (NP,NE)

- bài toán quay về tính góc PNE?

*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

Giải Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 độ đến 180 độ 

Đáp án đúng: C

*Lời giải:

Vẽ $\overrightarrow{BE}=\overrightarrow{AB}$.

Khi đó $\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\left(\overrightarrow{BE},\overrightarrow{BC}\right)=\widehat{CBE}=180-\widehat{CBA}={120}^0$

$\Rightarrow \cos \left(\overrightarrow{AB},\overrightarrow{BC}\right)=\cos {120}^0=-\frac{1}{2}.$

Tương tự, ta cũng có $\cos \left(\overrightarrow{BC},\overrightarrow{CA}\right)=\cos \left(\overrightarrow{CA},\overrightarrow{AB}\right)=-\frac{1}{2}.$

Vậy $\cos \left(\overrightarrow{AB},\overrightarrow{BC}\right)+\cos \left(\overrightarrow{BC},\overrightarrow{CA}\right)+\cos \left(\overrightarrow{CA},\overrightarrow{AB}\right)=-\frac{3}{2}$.

*Phương pháp giải:

- áp dụng công thức tính góc giữa hai vecto và áp dụng giá trị lượng giác để tìm ra giá trị biểu thức

*Lý thuyết nắm thêm về vectơ và giá trị lượng giác:

$(\overrightarrow{a},\overrightarrow{b})=(\overrightarrow{b},\overrightarrow{a})$

- Góc giữa hai vecto cùng hướng và khác 0 luôn bằng 0o

- Góc gữa hai vecto ngược hướng và khác $\overrightarrow{0}$ luôn bằng 180o

- Nếu $(\overrightarrow{u},\overrightarrow{v})$ = 90o thì ta nói $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau, kí hiệu là $\overrightarrow{u}\perp \overrightarrow{v}$ hoặc $\overrightarrow{v}\perp \overrightarrow{u}$. Đặc biệt $\overrightarrow{0}$ được coi là vuông góc với mọi vecto

- Góc không xác định nếu tồn tại 1 vecto không hay có thể nói góc bằng 0

- Cả hai vecto đều khác 0, tiến hành đưa về chung gốc để có thể tính toán.

- Cho hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$ và $\overrightarrow{OB}=\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$ ta có:

$(\overrightarrow{a},\overrightarrow{b})=\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$ ).

- Cho hai vectơ $\overrightarrow{a}=(a_1;a_2)$ và $\overrightarrow{b}=(b_1;b_2)$ đều khác vectơ $\overrightarrow{0}$ ta có:

$$\begin{gathered} \cos (\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1+a_2}.\sqrt{b_1+b_2}} \\ \overrightarrow{a}\perp \overrightarrow{b}\iff (\overrightarrow{a},\overrightarrow{b})={90}^o \\ \iff \overrightarrow{a}.\overrightarrow{b}=0 \\ \iff a_1.b_1+a_2.b_2=0 \end{gathered}$$

Cách tính góc giữa hai vecto

Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ

Định nghĩa góc giữa hai vectơ: Cho hai vectơ  đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .

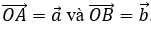
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ

Sử dụng công thức sau:

Cho hai vectơ 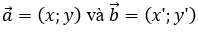. Khi đó

Chú ý: Góc giữa hai vectơ thuộc [0°;180°]

- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho  $\widehat{\mathrm{xOM}}=\alpha$. Khi đó:

+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là $\frac{y_0}{x_0}$, được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là $\frac{x_0}{y_0}$, được kí hiệu là cot α.

- Từ định nghĩa trên ta có:

$\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}(\alpha \ne 90°);$$\mathrm{cot\alpha }=\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}(\alpha \ne 0°\mathrm{và}\alpha \ne 180°);$$\mathrm{tan\alpha }=\frac{1}{\mathrm{cot\alpha }}\text{(}\alpha \notin \text{{}0°;90°;180°\text{}})$

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

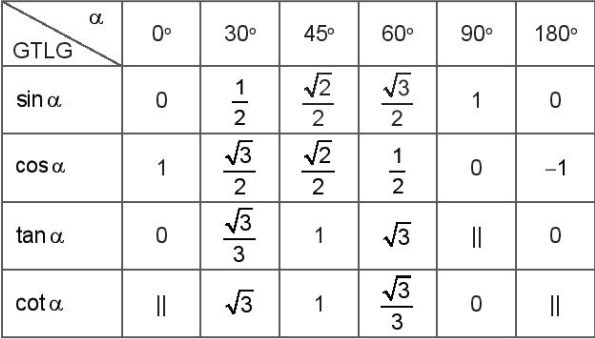
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = – cos α;

tan (180° – α) = – tan α  (α ≠ 90°);

cot (180° – α) = – cot α  (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau; có côsin, tang, côtang đối nhau.

- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Xem thêm các bài viết liên quan hay, chi tiết:

Công thức tính góc giữa hai vectơ (2024) chi tiết nhất

Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức 

Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ 

Vẽ $\overrightarrow{AE}=\overrightarrow{BA}$.

Vì tam giác ABC là tam giác đều nên đường cao AH đồng thời là  đường phân giác.

Suy ra:  $\widehat{BAH}=\frac{1}{2}\widehat{BAC}={30}^0$

Khi đó $\left(\overrightarrow{AH},\overrightarrow{AE}\right)=\widehat{HAE}=\alpha$ (hình vẽ)

          $={180}^0-\widehat{BAH}={180}^0-{30}^0={150}^0.$

Chọn D.                                        

Chọn D.

Tam giác ABC vuông ở A và có góc $\widehat{B}={50}^0\Rightarrow \widehat{ACB}={90}^0-{50}^0=40{}^0$

Vì $\left(\overrightarrow{AC},\overrightarrow{CB}\right)={180}^0-\widehat{ACB}={180}^0-{40}^0={140}^0.$

Xác định được $\left(\overrightarrow{AC},\overrightarrow{CB}\right)={180}^0-\widehat{ACB}.$

Ta có $\cos \widehat{ACB}=\frac{AC}{CB}=\frac{1}{2}\Rightarrow \widehat{ACB}={60}^0$

$\leftarrow \left(\overrightarrow{AC},\overrightarrow{CB}\right)={180}^0-\widehat{ACB}={120}^0$

Vậy $\cos \left(\overrightarrow{AC},\overrightarrow{CB}\right)=\cos {120}^0=-\frac{1}{2}.$ 

Chọn B.

Đáp án đúng: B.

*Lời giải

Ta có $\left\{\begin{array}{l}\left(\overrightarrow{AB},\overrightarrow{BC}\right)={180}^0-\widehat{ABC}\\ \left(\overrightarrow{BC},\overrightarrow{CA}\right)={180}^0-\widehat{BCA}\\ \left(\overrightarrow{CA},\overrightarrow{AB}\right)={180}^0-\widehat{CAB}\end{array}\right.$

$\begin{array}{l}\Rightarrow \left(\overrightarrow{AB},\overrightarrow{BC}\right)+\left(\overrightarrow{BC},\overrightarrow{CA}\right)+\left(\overrightarrow{CA},\overrightarrow{AB}\right)={540}^0-\left(\widehat{ABC}+\widehat{BCA}+\widehat{CAB}\right)\\ ={540}^0-{180}^0={360}^0.\end{array}$

*Phương pháp giải

- Xét tam giác ABC ta thấy: 

+ góc tạo bởi 2 vectơ ( AB,BC) = 180 - số đo góc ABC 

+ tương tự góc tạo bởi 2 cặp vectơ còn lại

- cộng lại với nhau để tìm ra kết quả

*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

Giải Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 độ đến 180 độ 

Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án

Ta có $\left\{\begin{array}{l}\left(\overrightarrow{AB},\overrightarrow{BC}\right)={180}^0-\widehat{ABC}\\ \left(\overrightarrow{BC},\overrightarrow{CA}\right)={180}^0-\widehat{BCA}\end{array}\right.$

$\Rightarrow \left(\overrightarrow{AB},\overrightarrow{BC}\right)+\left(\overrightarrow{BC},\overrightarrow{CA}\right)={360}^0-\left(\widehat{ABC}+\widehat{BCA}\right)$

$={360}^0-\left({180}^0-\widehat{BAC}\right)={360}^0-{180}^0+{60}^0={240}^0.$

ĐÁP ÁN D 

Vì $\widehat{HIA}+\text{}\widehat{HFA}={180}^0$ nên tứ giác HFAI nội tiếp.

Suy ra: $\widehat{IHF}+\text{}\widehat{IAF}={180}^0\Rightarrow \widehat{IHF}={180}^0-\text{}\widehat{IAF}={80}^0$