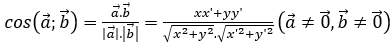Cho tam giác đều ABC. Tính $P=\cos \left(\overrightarrow{AB},\overrightarrow{BC}\right)+\cos \left(\overrightarrow{BC},\overrightarrow{CA}\right)+\cos \left(\overrightarrow{CA},\overrightarrow{AB}\right).$

Đáp án đúng: C

*Lời giải:

Vẽ $\overrightarrow{BE}=\overrightarrow{AB}$.

Khi đó $\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\left(\overrightarrow{BE},\overrightarrow{BC}\right)=\widehat{CBE}=180-\widehat{CBA}={120}^0$

$\Rightarrow \cos \left(\overrightarrow{AB},\overrightarrow{BC}\right)=\cos {120}^0=-\frac{1}{2}.$

Tương tự, ta cũng có $\cos \left(\overrightarrow{BC},\overrightarrow{CA}\right)=\cos \left(\overrightarrow{CA},\overrightarrow{AB}\right)=-\frac{1}{2}.$

Vậy $\cos \left(\overrightarrow{AB},\overrightarrow{BC}\right)+\cos \left(\overrightarrow{BC},\overrightarrow{CA}\right)+\cos \left(\overrightarrow{CA},\overrightarrow{AB}\right)=-\frac{3}{2}$.

*Phương pháp giải:

- áp dụng công thức tính góc giữa hai vecto và áp dụng giá trị lượng giác để tìm ra giá trị biểu thức

*Lý thuyết nắm thêm về vectơ và giá trị lượng giác:

$(\overrightarrow{a},\overrightarrow{b})=(\overrightarrow{b},\overrightarrow{a})$

- Góc giữa hai vecto cùng hướng và khác 0 luôn bằng 0o

- Góc gữa hai vecto ngược hướng và khác $\overrightarrow{0}$ luôn bằng 180o

- Nếu $(\overrightarrow{u},\overrightarrow{v})$ = 90o thì ta nói $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau, kí hiệu là $\overrightarrow{u}\perp \overrightarrow{v}$ hoặc $\overrightarrow{v}\perp \overrightarrow{u}$. Đặc biệt $\overrightarrow{0}$ được coi là vuông góc với mọi vecto

- Góc không xác định nếu tồn tại 1 vecto không hay có thể nói góc bằng 0

- Cả hai vecto đều khác 0, tiến hành đưa về chung gốc để có thể tính toán.

- Cho hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$ và $\overrightarrow{OB}=\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$ ta có:

$(\overrightarrow{a},\overrightarrow{b})=\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$ ).

- Cho hai vectơ $\overrightarrow{a}=(a_1;a_2)$ và $\overrightarrow{b}=(b_1;b_2)$ đều khác vectơ $\overrightarrow{0}$ ta có:

$$\begin{gathered} \cos (\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1+a_2}.\sqrt{b_1+b_2}} \\ \overrightarrow{a}\perp \overrightarrow{b}\iff (\overrightarrow{a},\overrightarrow{b})={90}^o \\ \iff \overrightarrow{a}.\overrightarrow{b}=0 \\ \iff a_1.b_1+a_2.b_2=0 \end{gathered}$$

Cách tính góc giữa hai vecto

Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ

Định nghĩa góc giữa hai vectơ: Cho hai vectơ  đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .

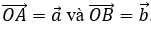
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ

Sử dụng công thức sau:

Cho hai vectơ 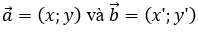. Khi đó

Chú ý: Góc giữa hai vectơ thuộc [0°;180°]

- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho  $\widehat{\mathrm{xOM}}=\alpha$. Khi đó:

+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là $\frac{y_0}{x_0}$, được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là $\frac{x_0}{y_0}$, được kí hiệu là cot α.

- Từ định nghĩa trên ta có:

$\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}(\alpha \ne 90°);$$\mathrm{cot\alpha }=\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}(\alpha \ne 0°\mathrm{và}\alpha \ne 180°);$$\mathrm{tan\alpha }=\frac{1}{\mathrm{cot\alpha }}\text{(}\alpha \notin \text{{}0°;90°;180°\text{}})$

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

 

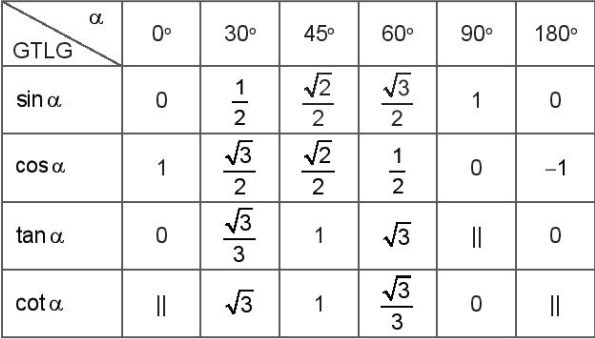
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = – cos α;

tan (180° – α) = – tan α  (α ≠ 90°);

cot (180° – α) = – cot α  (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau; có côsin, tang, côtang đối nhau.

 

- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Xem thêm các bài viết liên quan hay, chi tiết:

Công thức tính góc giữa hai vectơ (2024) chi tiết nhất

Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức 

Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ