Bài 8.12 trang 74 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Lời giải Bài 8.12 trang 74 Toán 10 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

1 9,819 21/11/2024

Trang trước

Trang sau

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.12 trang 74 Toán 10 Tập 2: Khai triển các đa thức:

a) (x – 3)⁴;

b) (3x – 2y)⁴;

c) (x + 5)⁴ + (x – 5)⁴;

d) (x – 2y)⁵.

Lời giải

Áp dụng các công thức khai triển của (a + b)⁴ và (a + b)⁵.

(a + b)⁴₌ $C_{4}^{0} a^{4} + C_{4}^{1} a^{3} b + C_{4}^{2} a^{2} b^{2} + C_{4}^{3} a b^{3} + C_{4}^{4} b^{4}$ = $a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$

(a+b)^{5₌ $C_{5}^{0} a^{5} + C_{5}^{1} a^{4} b + C_{5}^{2} a^{3} b^{2} + C_{5}^{3} a^{2} b^{3} + C_{5}^{4} a b^{4} + C_{5}^{5} b^{5}$}

^{= $a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$}

a) (x – 3)⁴

= x⁴ + 4 . x³ . (–3) + 6 . x² . (–3)² + 4 . x . (–3)³ + (–3)⁴

= x⁴ – 12x³ + 54x² – 108x + 81.

b) (3x – 2y)⁴

= (3x)⁴ + 4 . (3x)³ . (– 2y) + 6 . (3x)² . (– 2y)² + 4 . (3x) . (– 2y)³ + (– 2y)⁴

= 81x⁴ – 216x³y + 216x²y² – 96xy³ + 16y⁴.

c) (x + 5)⁴ + (x – 5)⁴

= (x⁴ + 4x³ . 5 + 6x² . 5² + 4x . 5³+ 5⁴) + [x⁴ + 4x³ . (– 5) + 6x² . (– 5)² + 4x . (– 5)³ + (– 5)⁴]

= (x⁴ + x⁴) + (20x³ – 20x³) + (150x² + 150x²) + (500x – 500x) + (625 + 625)

= 2x⁴ + 300x² + 1250.

d) (x – 2y)⁵

= x⁵ + 5x⁴ . (– 2y) + 10x³ . (– 2y)² + 10x² . (– 2y)³ + 5x . (2y)⁴ + (– 2y)⁵

= x⁵ – 10x⁴y + 40x³y² – 80x²y³ + 80xy⁴ – 32y⁵.

*Phương pháp giải:

Sử dụng công thức triển khai nhị thức

• ${(a + b)}^{4} = C_{4}^{0} a^{4} + C_{4}^{1} a^{3} b + C_{4}^{2} a^{2} b^{2} + C_{4}^{3} a b^{3} + C_{4}^{4} b^{4}$

$= a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4};$

*Lý thuyết:

1. Nhị thức Newton là gì?

Nhị thức Newton là một định lý toán học quan trọng liên quan đến khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý Nhị thức Newton có ứng dụng rộng rãi trong toán học và nhiều lĩnh vực khác, bao gồm:

+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ quan trọng trong việc tính toán số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, điều này có ứng dụng trong nhiều vấn đề tổ hợp và chỉnh hợp.

+ Dãy số: Định lý Nhị thức Newton thường được sử dụng để chứng minh các thuộc tính của các dãy số, ví dụ như dãy số Fibonacci và dãy số Pascal.

+ Xác suất và thống kê: Trong xác suất và thống kê, định lý Nhị thức Newton được sử dụng để tính xác suất và biểu diễn các phân phối xác suất, nhất là trong việc tính toán xác suất của các biến ngẫu nhiên rời rạc.

+ Lý thuyết đồ thị: Công thức Nhị thức được sử dụng để tính toán số lượng đồ thị con trong một đồ thị, điều này có ứng dụng trong lý thuyết đồ thị và các vấn đề liên quan đến mạng lưới.

2. Công thức Nhị thức Newton và khai triển

Với $a, b$ là những số thực tùy ý và với mọi số tự nhiên $n \geq 1$ , ta có:

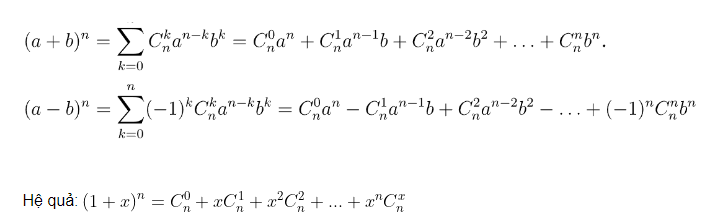
Lý thuyết Nhị thức Newton – Toán 10 Chân trời sáng tạo (ảnh 1)

Hai công thức khai triển:

• ${(a + b)}^{4} = C_{4}^{0} a^{4} + C_{4}^{1} a^{3} b + C_{4}^{2} a^{2} b^{2} + C_{4}^{3} a b^{3} + C_{4}^{4} b^{4}$

$= a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4};$

• ${(a + b)}^{5} = C_{5}^{0} a^{5} + C_{5}^{1} a^{4} b + C_{5}^{2} a^{3} b^{2} + C_{5}^{3} a^{2} b^{3} + C_{5}^{4} a b^{4} + C_{5}^{5} b^{5}$

$= a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5} .$

Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ${(a + b)}^{n}$ ứng với n = 4 và n = 5.

Chú ý:

– Các hệ số trong khai triển nhị thức Newton (a + b)ⁿ với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.

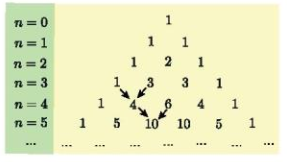
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).

Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).

Xem thêm

Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải

TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Mở đầu trang 72 Toán 10 Tập 2: Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: (a + b)² = a² + 2ab + b²; (a + b)³ = a³ + 3a²b + 3ab² + b³...

Hoạt động 1 trang 72 Toán 10 Tập 2: Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau: Từ một điểm gốc, kẻ các mũi tên...

Hoạt động 2 trang 72 Toán 10 Tập 2: Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b). Có bao nhiêu tích nhận được...

Hoạt động 3 trang 73 Toán 10 Tập 2: Sơ đồ hình cây của khai triển (a + b)⁴ được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 2⁴...

Luyện tập 1 trang 73 Toán 10 Tập 2: Khai triển (x – 2)⁴...

Hoạt động 4 trang 74 Toán 10 Tập 2: Tương tự như HĐ3, sau khi khai triển (a + b)⁵, ta thu được một tổng gồm 2⁵ đơn thức có dạng x . y . z . t . u...

Luyện tập 2 trang 74 Toán 10 Tập 2: Khai triển (3x – 2)⁵...