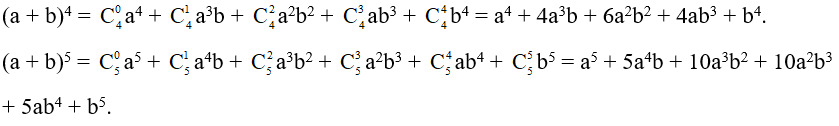Nội dung bài viết

    Xem thêm

    Lý thuyết Nhị thức Newton - Toán 10 Kết nối tri thức

    Với lý thuyết Toán lớp 10 Bài 25: Nhị thức Newton, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 10.

    1 1,151 14/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 10 Bài 25: Nhị thức Newton - Kết nối tri thức

    A. Lý thuyết Nhị thức Newton

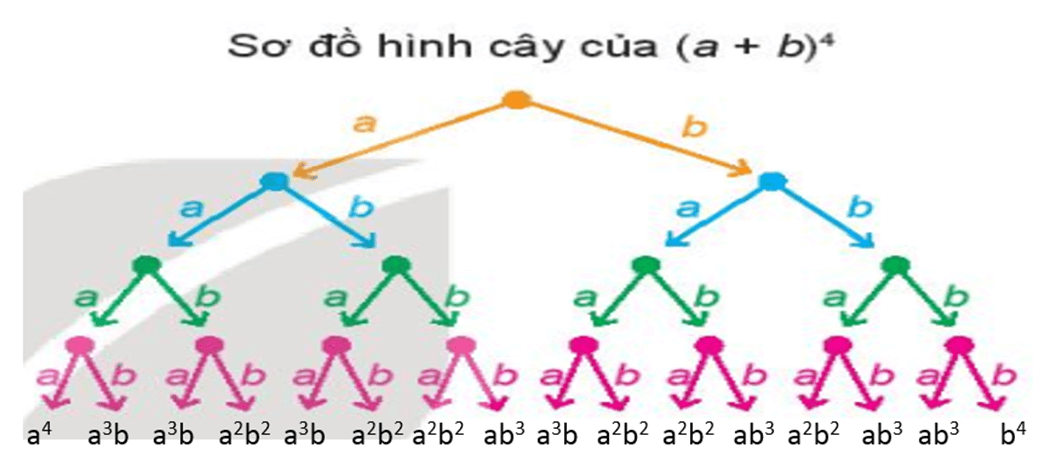
    Nhận xét: Các tích nhận được từ sơ đồ hình cây của một tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Tổng của chúng cho ta khai triển của tích các đa thức đã cho.

    Ví dụ: Sơ đồ hình cây của khai triển: (a + b)4

    Nhị thức Newton (Lý thuyết Toán lớp 10) | Kết nối tri thức

    Ta có: (a + b)4 = (a + b).(a + b).(a + b).(a + b)

    + Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ nhất là a và b.

    + Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai là a và b.

    + Làm tương tự cho đến nhị thức thứ tư.

    + Tại ngọn của mũi tên xây dựng tại bước cuối cùng, ta ghi lại các tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.

    Nhị thức Newton:

    Nhị thức Newton (Lý thuyết Toán lớp 10) | Kết nối tri thức

    Ví dụ:

    a) Khai triển (1 + x)4 ;

    b) Khai triển (2x – 3)5.

    Hướng dẫn giải

    a) Ta có :

    (1 + x)4 = C4014 + C4113.x + C4212x2 + C431.x3 + C44>x4

    = 14 + 4.13x + 6.12.x2 + 4.1.x3 + x4

    = 1 + 4x + 6x2 + 4x3 + x4.

    Vậy (1 + x)4 = 1 + 4x + 6x2 + 4x3 + x4.

    b) Ta có :

    (x + 3)5 = C50x5 + C51x4.3 + C52x3.32 + C53>x2.33 + C54x.34 + C5535

    = x5 + 5x4.3 + 10x3.32 + 10x2.33 + 5x.34 + 35

    = x5 + 15x4 + 90x3 + 270x2 + 405x + 243.

    Nhận xét: Các công thức khai triển (a + b)n với n ∈ {4 ; 5}, là một công cụ hiệu quả để tính chính xác hoặc xấp xỉ một số đại lượng mà không cần dùng máy tính.

    Ví dụ: Dùng hai số hạng đầu của khai triển (1 + 0,02)5 để tính giá trị gần đúng của 1,025.

    Hướng dẫn giải

    Ta có: (1 + 0,02)5 = 15 + 5.14. 0,02 + 10.13.0,022 + 10.12.0,023 + 5.1.0,024 + 0,025

    = 1 + 0,1 + 10.13.0,022 + 10.12.0,023 + 5.1.0,024 + 0,025.

    Vì 1 + 0,1 = 1,1 nên (1 + 0,02)5 ≈ 1,1, tức là 1,025 ≈ 1,1.

    Vậy 1,025 ≈ 1,1.

    B. Bài tập Nhị thức Newton

    1. Bài tập trắc nghiệm

    Câu 1. Khai triển (a + b)5 có tất cả bao nhiêu số hạng

    A. 4; 

    B. 5;

    C. 6;

    D. 7.

    Đáp án: C

    Giải thích:

    Ta có: (a + b)5  = a5 + 5a4b +10a3b2 + 10a2b3 + 5a4b + b5

    Khai triển có 6 phần tử.

    Câu 2. Cho khai triển (x + 3)5 = x5 + 15x4 + 90x3 + 270x2 + 405x + 243. Tổng các hệ số của khai triển đã cho là:

    A. 987;                 

    B. 784;

    C. 1000;

    D. 1024.

    Đáp án: D

    Giải thích:

    S = 1 + 15 + 90 + 270 + 405 + 243 = 1024.

    Câu 3. Ta có khai triển đa thức: (x – 1)4 = x4 − 4x3 + 6x2 − 4x + 1. Hệ số của hạng tử có chứa x3 là:

    A. 4;

    B. – 4;

    C. 6;

    D. – 6

    Đáp án: C

    Giải thích:

    Ta có: (x – 1)4 = x4 − 4x3 + 6x2 − 4x + 1.

    Số hạng chứa x3 là – 4x3

    Do đó hệ số của hạng tử chứa x3 là – 4.

    Câu 4. Khai triển đa thức (x + 3)4

    A. x4 + 4x3 + 6x2 + 4x + 1;                 

    B. x4 + 12x3 + 54x2 + 108x + 81;   

    C. x4 + 5x3 + 10x2 + 5x + 81;         

    D. x4 − 12x3 + 54x2 − 108x + 81.

    Đáp án: B

    Giải thích:

    Áp dụng công thức triển khai của (a + b)4 với a = x, b = 3 ta có:

    (x + 3)4 = x4 + 4x3 .3 + 6x2.32 + 4x.33 + 34 = x4 + 12x3 + 54x2 + 108x + 81.

    Câu 5. Khai triển đa thức: (2x - 1)4

    A. 16x4 − 32x3 + 24x2 − 8x + 1;          

    B. 16x4 + 32x3 + 24x2 + 8x + 1;     

    C. 16x4 − 32x3 + 24x2 + 8x + 1;     

    D. 16x4 + 32x3 + 24x2 − 8x + 1.

    Đáp án: A

    Giải thích:

    Áp dụng công thức triển khai của (a + b)4 với a = 2x, b = −1 ta có:

    (2x − 1)4 = (2x)4 + 4(2x)3.(−1) + 6(2x)2.(−1)2 + 4.2x.(−1)3 + (−1)4

    = 16x4 − 32x3 + 24x2 − 8x + 1.

    2. Bài tập tự luận

    Bài 1: Khai triển các đa thức sau:

    a) (2x – 1)4 ;

    b) (x + 4)5 + (x – 4)5.

    Hướng dẫn giải

    a) Ta có: (2x – 1)4 = (2x)4 + 4(2x)3.(–1) + 6(2x)2.(–1)2 + 4.2x.(–1)3 + (–1)4.

    = 16x4 – 32x3 + 24x2 – 8x + 1.

    Vậy : (2x – 1)4 = 16x4 – 32x3 + 24x2 – 8x + 1.

    b) Ta có:

    (x + 4)5 + (x – 4)5 = [x5 + 5x4.4 + 10.x3.42 + 10.x2.43 + 5.x.44 + 45] + [x5 + 5x4.(–4) + 10.x3.(–4)2 + 10.x2.(–4)3 + 5.x.(–4)4 + (–4)5]

    = [x5 + 20x4 + 160x3 + 640x2 + 1280x + 1024] + [x5 – 20x4 + 160x3 – 640x2 + 1280x –1024]

    = x5 + 20x4 + 160x3 + 640x2 + 1280x + 1024 + x5 – 20x4 + 160x3 – 640x2 + 1280x –1024 = 2x5 + 320x3 + 2560x.

    Vậy (x + 4)5 + (x – 4)5 = 2x5 + 320 x3 + 2560x.

    Bài 2 :

    a) Dùng hai số hạng đầu của khai triển (2 + 0,01)4 để tính giá trị gần đúng của 2,014.

    b) Dùng máy tính cầm tay để tính giá trị của 2,014 và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

    Hướng dẫn giải

    a) Ta có:(2 + 0,01)4 = 24 + 4.23.0,01 + 6.22.0,012 + 4.2.0,013 + 0,014

    = 16 + 0,32 + 6.22.0,012 + 4.2.0,013 + 0,014

    Vì 16 + 0,32 = 16,32 nên (2 + 0,01)4 ≈ 16,32, tức là 2,014 ≈ 16,32.

    Vậy 2,014 ≈ 16,32.

    b) Dùng máy tính cầm tay ta tính được giá trị của 2,014 = 16,32240801....

    Ta có: 16,32 < 2,014 <16,33

    Suy ra: |16,32 – 2,014| < |16,33 – 16, 32| = 0,01.

    Vậy với giá trị gần đúng 16,32 thì sai số tuyệt đối không vượt quá 0,01.

    Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài 23: Quy tắc đếm

    Lý thuyết Bài 24: Hoán vị, chỉnh hợp và tổ hợp

    Lý thuyết Bài 26: Biến cố và định nghĩa cổ điển của xác suất

    Lý thuyết Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

    Tổng hợp lý thuyết Chương 9

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,151 14/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: