Lý thuyết Ba đường conic - Toán 10 Kết nối tri thức

Lý thuyết Toán 10 Bài 22: Ba đường conic - Kết nối tri thức

 

A. Lý thuyết Ba đường conic

1. Elip

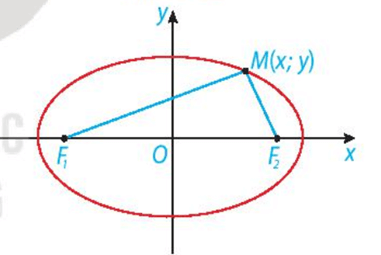
- Cho hai điểm cố định và phân biệt F₁, F₂. Đặt F₁F₂ = 2c > 0. Cho số thực a lớn hơn c. Tập hợp các điểm M sao cho MF₁ + MF₂ = 2a được gọi là đường elip (hay elip). Hai điểm F₁, F₂ được gọi là hai tiêu điểm và F₁F₂ = 2c được gọi là tiêu cự của elip đó.

- Trong mặt phẳng tọa độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm, thì có phương trình

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, với a > b > 0. (2)

Ngược lại, mỗi phương trình có dạng (2) đều là phương trình của elip có hai tiêu điểm F₁( $-\sqrt{a^2-b^2}$; 0), F₂($\sqrt{a^2-b^2}$ ; 0), tiêu cự 2c = $2\sqrt{a^2-b^2}$ và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a.

Phương trình (2) được gọi là phương trình chính tắc của elip tương ứng.

Ví dụ: Cho elip có phương trình chính tắc $\frac{x^2}{9}+\frac{y^2}{4}=1$ . Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.

Hướng dẫn giải

Ta có a² = 9 ⇒ a = 3 (do a > 0) và b² = 4. Do đó $c=\sqrt{a^2-b^2}=\sqrt{9-4}=\sqrt{5}$.

Khi đó hai tiêu điểm là F₁( $-\sqrt{5}$; 0); F₂( $\sqrt{5}$; 0). Tiêu cự F₁F₂ = 2c = $2\sqrt{5}$

Tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a = 2.3 = 6.

Vậy hai tiêu điểm của elip là F₁($-\sqrt{5}$; 0); F₂( $\sqrt{5}$; 0); tiêu cự F₁F₂ = $2\sqrt{5}$; tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 6.

2. Hypebol

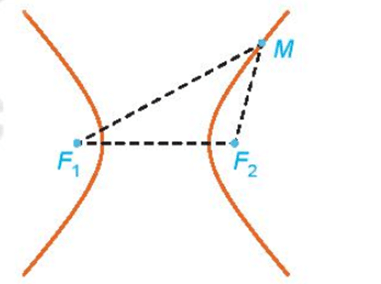
- Cho hai điểm phân biệt cố định F₁ và F₂. Đặt F₁F₂ = 2c. Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a được gọi là đường hypebol (hay hypebol). Hai điểm F₁, F₂ được gọi là hai tiêu điểm và F₁F₂ = 2c được gọi là tiêu cự của hypebol đó.

Chú ý: Hypebol có hai nhánh, một nhánh gồm những điểm M thỏa mãn MF₁ – MF₂ = 2a và nhánh còn lại gồm những điểm M thỏa mãn MF₁ – MF₂ = – 2a (hay MF₂ – MF₁ = 2a).

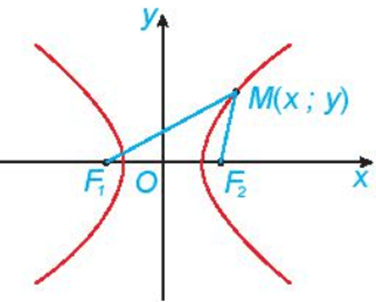
- Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, với a, b > 0. (4)

- Ngược lại, mỗi phương trình có dạng (4), đều là phương trình của hypebol có hai tiêu điểm F₁( $-\sqrt{a^2+b^2}$; 0), F₂( $\sqrt{a^2+b^2}$; 0), tiêu cự 2c = $2\sqrt{a^2+b^2}$ và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng 2a.

Phương trình (4) được gọi là phương trình chính tắc của hypebol tương ứng.

Ví dụ: Cho hypebol có phương trình chính tắc $\frac{x^2}{4}-\frac{y^2}{9}=1$ . Tìm các tiêu điểm và tiêu cự của hypebol đó. Hiệu khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

Hướng dẫn giải

Ta có a² = 4, b² = 9, nên $c=\sqrt{a^2+b^2}=\sqrt{4+9}=\sqrt{13}$

Do đó hypebol có hai tiêu điểm F₁ ($-\sqrt{13}$ ; 0), F₂ ($\sqrt{13}$ ; 0) và có tiêu cự F₁F₂ = 2c = $2\sqrt{13}$ .

Hiệu khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng 2a = 2.2 = 4.

Vậy hypebol có hai tiêu điểm F₁( $-\sqrt{13}$; 0), F₂( $\sqrt{13}$; 0); tiêu cự F₁F₂ = $2\sqrt{13}$ ; hiệu khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng 4.

3. Parabol

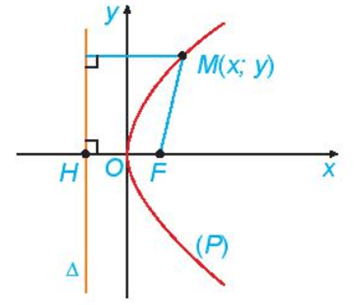
- Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F. Tập hợp các điểm M cách đều F và ∆ được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, ∆ được gọi là đường chuẩn, khoảng cách từ F đến ∆ được gọi là tham số tiêu của parabol đó.

- Xét (P) là một parabol với tiêu điểm F, đường chuẩn ∆. Gọi H là hình chiếu vuông góc của F trên ∆. Khi đó, trong hệ trục tọa độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình y² = 2px (với p > 0) (5)

Phương trình (5) được gọi là phương trình chính tắc của parabol (P).

Ngược lại, mỗi phương trình dạng (5), với p > 0, là phương trình chính tắc của parabol có tiêu điểm $F\left(\frac{p}{2};0\right)$ và đường chuẩn ∆: $x=-\frac{p}{2}$

Ví dụ: Cho parabol (P): y² = 4x. Tìm tiêu điểm F, đường chuẩn ∆ của (P).

Hướng dẫn giải

Ta có 2p = 4 nên p = 2 ⇒ $\frac{p}{2}=\frac{2}{2}=1$

Khi đó parabol có tiêu điểm F(1; 0) và đường chuẩn ∆: $x=-\frac{p}{2}=-1$.

Vậy parabol có tiêu điểm F(1 ; 0) và đường chuẩn ∆: x = –1.

4. Một số ứng dụng của ba đường conic

* Tính chất quang học

Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương (lồi, lõm) elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phản xạ theo một quy tắc được xác định rõ ràng bằng hình học, chẳng hạn:

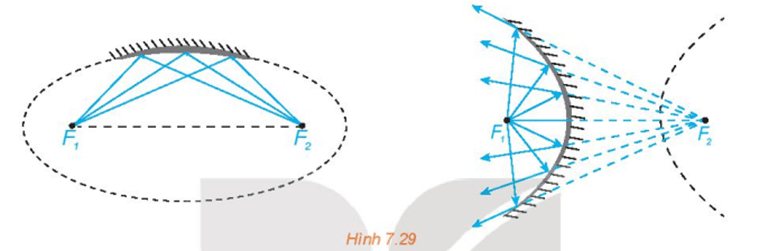
- Tia sáng phát ra từ một tiêu điểm của elip, hypebol (đối với các gương lõm elip, hypebol) sau khi gặp elip, hypebol sẽ bị hắt lại theo một tia (tia phản xạ) nằm trên đường thẳng đi qua tiêu điểm còn lại (H.7.29).

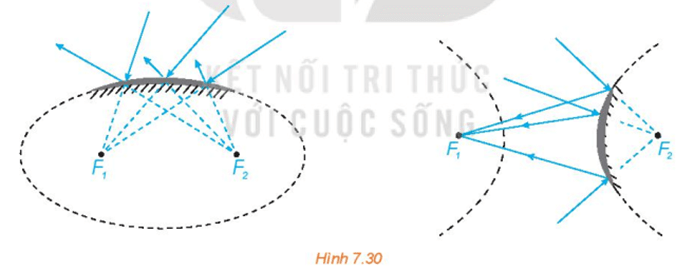
- Tia sáng hướng tới một tiêu điểm của elip, hypebol (đối với các gương elip, hypebol lồi), khi gặp elip, hypebol sẽ bị hắt lại theo một tia nằm trên đường thẳng đi qua tiêu điểm còn lại (H.7.30).

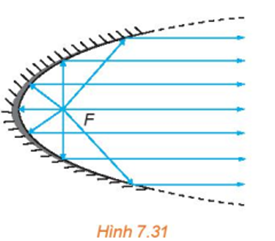
- Với gương parabol lõm, tia sáng phát ra từ tiêu điểm khi gặp parabol sẽ bị hắt lại theo một tia vuông góc với đường chuẩn của parabol (H.7.31). Ngược lại, nếu tia tới vuông góc với đường chuẩn của parabol thì tia phản xạ sẽ đi qua tiêu điểm của parabol.

Tính chất quang học giúp ta nhận được ánh sáng mạnh hơn khi các tia sáng hội tụ và giúp ta đổi hướng ánh sáng khi cần. Ta cũng có điều tương tự đối với tín hiệu âm thanh, tín hiệu truyền từ vệ tinh.

* Một số ứng dụng

Ba đường conic xuất hiện và có nhiều ứng dụng trong khoa học và trong cuộc sống, chẳng hạn:

+ Tia nước bắn ra từ đài phun nước, đường đi bổng của quả bóng là những hình ảnh về đường parabol;

+ Khi nghiêng cốc nước tròn, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của một quả bóng, nhìn chung là một elip;

+ Ánh sáng phát ra từ một bóng đèn Led trên trần nhà có thể tạo nên trên tường các nhánh hypebol;

+ Nhiều công trình kiến trúc có hình elip, parabol hay hypebol.

+ Trong vũ trụ bao la, ánh sáng đóng vai trò sứ giả truyền tin. Ánh sáng phát ra từ một thiên thể sẽ mang những thông tin về nơi nó xuất phát. Khi nhận được ánh sáng, các nhà khoa học sẽ dựa vào đó để nghiên cứu, khám phá thiên thể. Trong thiên văn học, các gương trong kính thiên văn (H.7.32a) giúp nhà khoa học nhận được hình ảnh quan sát rõ nét hơn, ánh sáng thu được có các chỉ số phân tích rõ hơn.

+ Ăng-ten vệ tinh parabol (H.7.32b) là thiết bị thu tín hiệu truyền về từ vệ tinh. Tín hiệu sau khi gặp parabol bị hắt lại và hội tụ về điểm thu được đặt tại tiêu điểm của parabol.

+ Đèn pha đáy parabol (H.7.32c) giúp ánh sáng có thể phát xa (chẳng hạn giúp đèn ô tô có thể chiếu xa). Ánh sáng xuất phát từ vị trí tiêu điểm của parabol, chiếu vào đáy đèn, các tia sáng bị hắt lại thành các tia sáng nằm trên các đường thẳng song song.

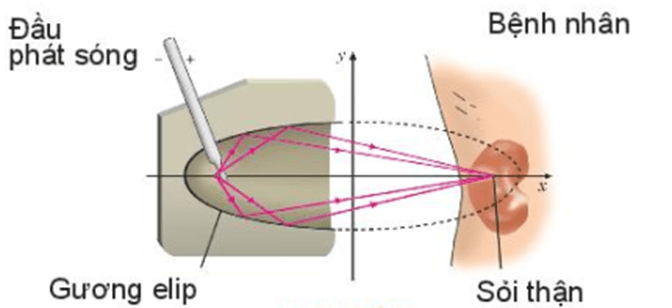
+ Trong y học, để tán sỏi thận, người ta có thể dùng chùm tia laser phát ra từ một tiêu điểm của gương elip để sau khi phản xạ sẽ hội tụ lại tiêu điểm còn lại cũng chính là vị trí sỏi.

+ Tháp giải nhiệt hình hypebol trong lò phản ứng hạt nhân hay trong nhà máy nhiệt điện có kiến trúc đảm bảo độ vững chãi, tiết kiệm nguyên vật liệu và giúp quá trình tỏa nhiệt được thuận lợi.

+ Bằng các quan sát và phân tích thiên văn, Johannes Kepler (1571 – 1630) đã đưa ra định luật nói rằng, các hành tinh trong hệ Mặt Trời chuyển động theo các quỹ đạo là các đường elip nhận tâm Mặt Trời là một tiêu điểm.

Ví dụ: Gương elip trong một máy tán sỏi thận ứng với elip có phương trình chính tắc là $\frac{x^2}{484}+\frac{y^2}{84}=1$ (đơn vị cm)

Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Hướng dẫn giải

Từ phương trình của elip $\frac{x^2}{484}+\frac{y^2}{84}=1$ ta có a² = 484, b² = 84.

Khi đó $c=\sqrt{a^2-b^2}=\sqrt{484-84}=\sqrt{400}=20$ .

Tiêu cự của elip bằng 2c = 2.20 = 40.

Khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán chính là tiêu cự của elip và bằng 40 cm.

Vậy khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán là 40 cm.

B. Bài tập Ba đường conic

1. Bài tập trắc nghiệm

Câu 1. Phương trình nào là phương trình chính tắc của elip

A. $\frac{x^2}{1}+\frac{y^2}{6}=1$;               

B. $\frac{x^2}{144}-\frac{y^2}{25}=1$; 

C. $\frac{x^2}{16}+\frac{y^2}{4}=1$;   

D. $\frac{x^2}{36}+\frac{y^2}{4}=-1$.

Hiển thị đáp án  

Đáp án: C

Giải thích:

$\frac{x^2}{1}+\frac{y^2}{6}=1$ có a = 1; b = $\sqrt{6}$ mà a < b không thoả mãn điều kiện a > b > 0 nên $\frac{x^2}{1}+\frac{y^2}{6}=1$ không là phương trình chính tắc của đường elip. Do đó A sai

$\frac{x^2}{144}-\frac{y^2}{25}=1$ là phương trình hypebol nên B sai

$\frac{x^2}{36}+\frac{y^2}{4}=-1$ không có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ nên không là phương trình đường elip. Do đó D sai

$\frac{x^2}{16}+\frac{y^2}{4}=1$ có a = 4 ; b = 1 và a > b nên $\frac{x^2}{16}+\frac{y^2}{4}=1$ là phương trình elip. Do vậy C đúng

Câu 2. Hai tiêu điểm của hypebol $\frac{x^2}{16}-\frac{y^2}{9}=1$

A. F₁ (−3; 0) và F₂ (3; 0);                    

B. F₁ (−4; 0) và F₂ (4; 0);               

C. F₁ (−5; 0) và F₂ (5; 0);               

D. F₁ (−6; 0) và F₂ (6; 0).      

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có: $\frac{x^2}{16}-\frac{y^2}{9}=1$ ⇒ a = 4; b = 3

Ta có: c = $\sqrt{a^2+b^2}=\sqrt{4^2+3^2}=5$

Vậy hai tiêu điểm F₁ (−5; 0) và F₂ (5; 0).

Câu 3. Đường chuẩn của parabol y²  = 6x

A. ∆: x = $\frac{-3}{2}$;                 

B. ∆: x = $\frac{3}{2}$;       

C. ∆: x = 3;        

D. ∆: x = − 3.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có : y²  = 6x ⇒ p = 3

Vậy đường chuẩn ∆ : x = $\frac{-p}{2}$ = $\frac{-3}{2}$ .

Câu 4. Elip (E) : $\frac{x^2}{9}+\frac{y^2}{4}=1$ có tiêu cự bằng:

A. $\sqrt{5}$;                  

B. 10;

C. 5;

D. 2$\sqrt{5}$.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có: $\frac{x^2}{9}+\frac{y^2}{4}=1\iff \frac{x^2}{3^2}+\frac{y^2}{2^2}=1$ có a = 3; b = 2

Vậy tiêu cự (E) là: F₁F₂ = 2c = 2$\sqrt{a^2-b^2}$= 2$\sqrt{3^2-2^2}$= 2$\sqrt{5}$

Câu 5. Phương trình nào sau đây là phương trình chính tắc của parabol?

A. y² = −2x;                    

B. y² = $\frac{1}{-\sqrt{2}}$x;   

C. y² = $\left(\sqrt{2}-\sqrt{3}\right)$x;                      

D. y² = 5x.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Parabol (P) có phương trình y² = 2px (p > 0)

Với điều kiện p > 0 thì đáp án A; B; C sai và đáp án D: y² = 5x có p = $\frac{5}{2}>0$

Do đó y² = 5x là phương trình chính tắc của parabol.

2. Bài tập tự luận

Bài 1. Cho hypebol có phương trình là $\frac{x^2}{36}-\frac{y^2}{64}=1$ . Hãy tìm tiêu điểm và tiêu cự của hypebol đó.

Hướng dẫn giải

Ta có a² = 36, b² = 64, nên $c=\sqrt{a^2+b^2}=\sqrt{64+36}=\sqrt{100}=10$.

Vậy hypebol có hai tiêu điểm là F₁(–10 ;0), F₂ (10; 0) và có tiêu cự là F₁F₂ = 2c = 2.10 = 20.

Bài 2. Lập phương trình chính tắc của elip (E) biết A(0 ; –2) là một điểm thuộc elip và F₁(1; 0) là một tiêu điểm của elip (E).

Hướng dẫn giải

Elip (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với a > b > 0.

Vì A ∈ (E) nên ta có : $\frac{0^2}{a^2}+\frac{{(-2)}^2}{b^2}=1$⇒ b = 2 (do b > 0).

Vì (E) có tiêu điểm F₁(1 ; 0) nên c = 1.

Mặt khác 2c = $2\sqrt{a^2-b^2}$ ⇒ c² = a² – b²

⇒ a² = c² + b² = 1² + 2² = 5

⇒ a = $\sqrt{5}$ (do a > 0).

Vậy phương trình chính tắc của elip (E) là $\frac{x^2}{5}+\frac{y^2}{4}=1$ .

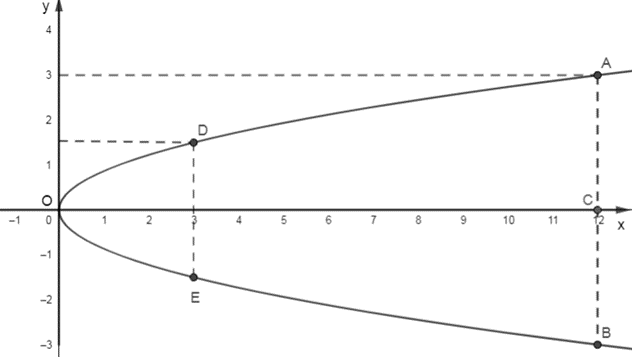
Bài 3. Một cổng chào có hình parabol cao 12 m và bề rộng của cổng tại chân cổng là 6 m. Tính bề rộng của cổng tại chỗ cách đỉnh 3 m.

Hướng dẫn giải

Vì cổng chào có hình parabol nên ta chọn hệ trục tọa độ như hình vẽ sau:

Gọi phương trình của parabol là: y² = 2px

Ta có chiều cao của cổng là OC = 12 m ⇒ C(12; 0)

Bề rộng của cổng tại chân cổng là AB = 6m ⇒ AC = 3m ⇒ A(12 ; 3).

Vì A(12; 3) thuộc parabol nên thay tọa độ A vào phương trình y² = 2px ta được:

3² = 2p.12

⇒ p = $\frac{9}{24}=\frac{3}{8}$ ⇒ y² = $\frac{3}{4}$ x.

Với điểm D(3; a) thuộc parabol: Thay tọa độ điểm D vào phương trình của parabol, ta được a² = $\frac{3}{4}$ .3 = $\frac{9}{4}$ ⇒ a = $\frac{3}{2}$ .

⇒ D(3; $\frac{3}{2}$ ).

Suy ra DE = 2a = 2. $\frac{3}{2}$ = 3 (m).

Vậy bề rộng của cổng tại chỗ cách đỉnh 3 m là 3 (m).

Bài 4. Một tháp làm nguội của một nhà máy có mặt cắt là một hypebol có phương trình $\frac{x^2}{{25}^2}-\frac{y^2}{{40}^2}=1$ . Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{2}{3}$ khoảng cách từ tâm đối xứng đến đáy. Chọn hệ trục toạ độ như hình vẽ dưới đây, tính bán kính nóc và bán kính đáy của tháp. (Làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Theo bài ra, khoảng cách từ nóc tháp đến tâm O bằng $\frac{2}{3}$ khoảng cách từ tâm O đến đáy nên ta có: OA = $\frac{2}{3}$ OB và OA + OB = 120 m.

Suy ra: OA = 48 m, OB = 72 m.

⇒ A (0; 48), B(0 ; –72).

Thay y = 48 vào phương trình $\frac{x^2}{{25}^2}-\frac{y^2}{{40}^2}=1$ , ta được:

$\frac{x^2}{{25}^2}-\frac{{48}^2}{{40}^2}=1$⇒ x² = 1 525 ⇒ x ≈ 39,1 hoặc x ≈ –39,1.

Suy ra bán kính nóc khoảng 39,1 (m).

Thay y = –72 vào phương trình $\frac{x^2}{{25}^2}-\frac{y^2}{{40}^2}=1$ ta được:

$\frac{x^2}{{25}^2}-\frac{{(-72)}^2}{{40}^2}=1$ ⇒ x² = 2 650 ⇒ x ≈ 51,5 hoặc x ≈ –51,5.

Suy ra bán kính đáy khoảng 51,5 (m).

Vậy bán kính nóc và bán kính đáy của tháp lần lượt là 39,1 (m) và 51,5 (m).

Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Kết nối tri thức hay, chi tiết khác:

Tổng hợp lý thuyết Chương 7

Lý thuyết Bài 23: Quy tắc đếm

Lý thuyết Bài 24: Hoán vị, chỉnh hợp và tổ hợp

Lý thuyết Bài 25: Nhị thức Newton

Lý thuyết Bài 26: Biến cố và định nghĩa cổ điển của xác suất