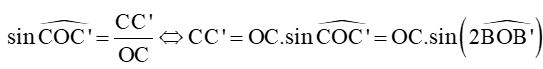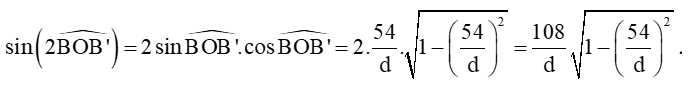Giải Toán 11 trang 20 Tập 1 Chân trời sáng tạo

Với giải bài tập Toán 11 trang 20 Tập 1 trong Bài 2: Giá trị lượng giác của một góc lượng giác sách Chân trời sáng tạo Tập 1 hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 20 Tập 1.

1 515 22/03/2023

Trang trước

Trang sau

Giải Toán 11 trang 20 Tập 1

Bài 7 trang 20 Toán 11 Tập 1: Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được $3 \frac{1}{10}$ vòng là bao nhiêu, biết độ dài thanh OM là 15 cm? Kết quả làm tròn đến hàng phần mười.

Lời giải:

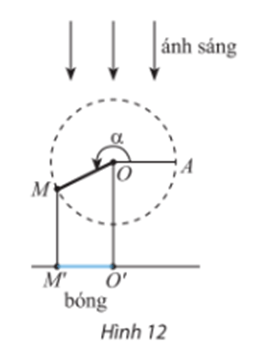
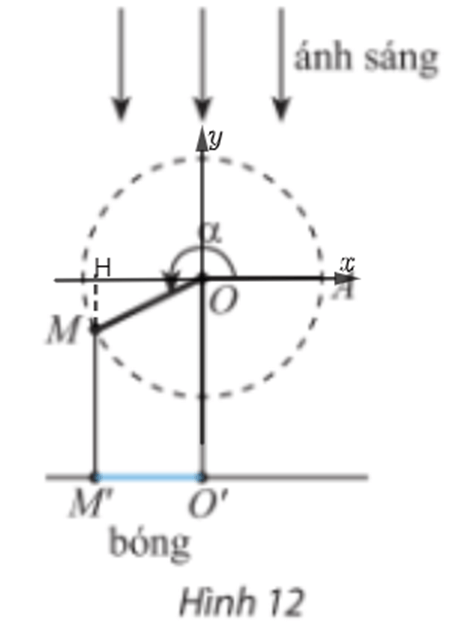
Đặt hệ trục tọa độ như hình vẽ:

Bài 7 trang 20 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Kẻ MH vuông góc với Ox.

Điểm M là điểm biểu diễn góc lượng giác α

Ta có: $α = 3 \frac{1}{10} .360 ° = 1 116 °$

Khi đó M(cos1116°.15; sin1116°.15)

Suy ra OH = |cos1116°|.15 ≈12,1.

Vậy độ dài bóng O’M’ của OM khi thanh quay được $3 \frac{1}{10}$ vòng là 12,1 cm.

Bài 8 trang 20 Toán 11 Tập 1: Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển , khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dàu của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Lời giải:

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: α = 11.60 = 660 (rad).

Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là:

V(58.cosα; 58.sinα) ≈ (56; 15,2)

Khi đó khoảng cách từ van đến mặt đất khoảng 58 – 15,2 = 42,8 cm.

Hoạt động khởi động trang 20 Toán 11 Tập 1: Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

Lời giải:

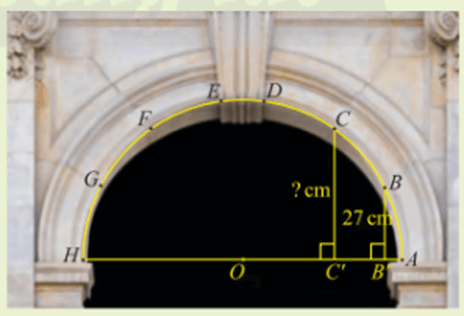
Đặt chiều rộng cổng AH = d.

⇒ OA = OB = $\frac{1}{2}$ d.

Xét tam giác OBB’ vuông tại B’, có:

$\sin \hat{B O B'} = \frac{B B'}{O B} = \frac{27}{\frac{d}{2}} = \frac{54}{d}$ .

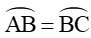
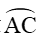
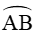
Vì Hoạt động khởi động trang 20 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 nên sđ = 2.sđ $\Rightarrow \hat{A O C} = 2 \hat{B O B'}$

Xét tam giác OCC’ vuông tại C’, có:

Hoạt động khởi động trang 20 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:

Hoạt động khởi động trang 20 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy khoảng cách này từ điểm C đến AH là $\frac{108}{d} \sqrt{1 - {(\frac{54}{d})}^{2}}$

Xem thêm lời giải bài tập Toán 11 sách Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 11 trang 13 Tập 1

Giải Toán 11 trang 15 Tập 1

Giải Toán 11 trang 16 Tập 1

Giải Toán 11 trang 17 Tập 1

Giải Toán 11 trang 19 Tập 1

Giải Toán 11 trang 20 Tập 1

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox...

Hoạt động khám phá 1 trang 13 Toán 11 Tập 1: Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{2 π}{3}$ và $- \frac{π}{4}$ trên đường tròn lượng giác...

Thực hành 1 trang 15 Toán 11 Tập 1: Tính sin $(- \frac{2 π}{3})$ và tan495°...

Thực hành 2 trang 16 Toán 11 Tập 1: Sử dụng máy tính cầm tay để tính cos75° và tan $(\frac{- 19 π}{6})$ ...

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1: a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin²α + cos²α = 1...

Thực hành 3 trang 17 Toán 11 Tập 1: Cho tan $α = \frac{2}{3}$ với $π < α < \frac{3 π}{2}$ . Tính cosα và sinα...

Hoạt động khám phá 3 trang 17 Toán 11 Tập 1: Cho $α = \frac{π}{3}$ . Biểu diễn các góc lượng giác – α, α + π, π – α, $\frac{π}{2} - α$ trên đường tròn lượng giác...

Thực hành 4 trang 19 Toán 11 Tập 1: a) Biểu diễn cos638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°...

Vận dụng trang 19 Toán 11 Tập 1: Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C...

Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không? a) sinα = $\frac{3}{5}$ và cosα = $- \frac{4}{5}$ ;...

Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = $\frac{12}{13}$ và cosα = $- \frac{5}{13}$ . Tính $\sin (- \frac{15 π}{2} - α) - cos (13 π + α)$ ...

Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu: a) sin $α$ = $\frac{5}{13}$ và $\frac{π}{2} < α < π$ ;...

Bài 4 trang 19 Toán 11 Tập 1: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{π}{4}$ hoặc từ 0 đến 45° và tính...

Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau: a) sin⁴α – cos⁴α = 1 – 2cos²α;...

Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau...

Bài 7 trang 20 Toán 11 Tập 1: Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12...

Bài 8 trang 20 Toán 11 Tập 1: Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13)...

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

1 515 22/03/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: