Giải Toán 10 trang 88 Tập 1 | Kết nối tri thức Giải Toán lớp 10

Giải Toán 10 trang 88 Tập 1

Bài 5.11 trang 88 Toán 10 Tập 1: Mỗi khẳng định sau đúng hay sai?

(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.

(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại.

(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.

(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.

(5) Các số đo độ phân tán đều không âm.

Lời giải:

∙ Khẳng định (1): Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị so với giá trị trung bình càng nhỏ (tức là $x_i-\overline{x}$ càng nhỏ, với i = 1; 2; ...; n), dẫn đến độ lệch chuẩn càng nhỏ.

Do đó, khẳng định (1) sai.

∙ Khẳng định (2): Khoảng biến thiên R bằng hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất nên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất.

Do đó, khẳng định (2) đúng.

∙ Khẳng định (3): Khoảng tứ phân vị Δ_Q = Q₃ − Q₁, các giá trị Q₁, Q₃ không bị ảnh hưởng bởi giá trị của giá trị lớn nhất và giá trị nhỏ nhất (với n > 4).

Do đó, khẳng định (3) sai.

∙ Khẳng định (4): Khoảng tứ phân vị chính là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp

Do đó, khẳng định (4) sai.

∙ Khẳng định (5): Các số đo độ phân tán là:

Khoảng biến thiên R = Số lớn nhất – Số nhỏ nhất > 0

Trước khi tính khoảng tứ phân vị thì mẫu số liệu được sắp xếp theo thứ tự không giảm

$\Rightarrow$ Q₃ > Q₁ $\Rightarrow$ Δ_Q = Q₃ − Q₁ > 0

Phương sai: $s^2=\frac{{(x_1-\overline{x})}^2+{(x_2-\overline{x})}^2+\mathrm{...}+{(x_n-\overline{x})}^2}{n}>0$

Độ lệch chuẩn: $s=\sqrt{s^2}>0$

Do đó, các số đo độ phân tán đều không âm

Do đó, khẳng định (5) đúng.

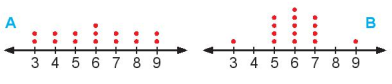
Bài 5.12 trang 88 Toán 10 Tập 1: Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:

Không tính toán, hãy cho biết:

a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?

b) Mẫu số liệu nào có phương sai lớn hơn?

Lời giải:

a) Ta có cả hai mẫu số liệu đều có giá trị nhỏ nhất là 3, giá trị lớn nhất là 9.

Do đó cả hai mẫu số liệu có cùng khoảng biến thiên.

Hai biểu đồ này có dạng đối xứng qua điểm 6 nên giá trị trung bình của hai mẫu số liệu A và B bằng nhau và bằng 6.

b) Từ biểu đồ, ta thấy các giá trị của dãy số liệu B tập trung nhiều hơn quanh giá trị trung bình nên mẫu số liệu B có phương sai nhỏ hơn. Vậy mẫu số liệu A có phương sai lớn hơn.

Bài 5.13 trang 88 Toán 10 Tập 1: Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:

a) Nhân mỗi giá trị của mẫu số liệu với 2.

b) Cộng mỗi giá trị của mẫu số liệu với 2.

Lời giải:

a) Gọi các giá trị dương của mẫu số liệu ban đầu theo thứ tự không giảm là:

Ta có n = 10 là số chẵn nên trung vị là giá trị trung bình của số thứ 5 và thứ 6.

Do đó Q₁ là số thứ 3 và Q₃ là số thứ 8.

a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì

+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần nên khoảng biến thiên R tăng 2 lần.

+ Q₁ và Q₃ tăng 2 lần nên khoảng tứ phân vị Δ_Q = Q₃ − Q₁ tăng 2 lần.

+ Giá trị trung bình tăng 2 lần.

Nên độ lệch của mỗi giá trị so với giá trị trung bình $|x_i-\overline{x}|$ cũng tăng 2 lần.

Suy ra ${(x_i-\overline{x})}^2$ tăng 4 lần.

Khi đó, phương sai tăng 4 lần.

Do đó độ lệch chuẩn tăng 2 lần.

Vậy các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị của dãy số liệu mới bằng hai lần các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị ban đầu.

b) Khi cộng mỗi giá trị của mẫu số liệu với 2 thì

+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị.

Suy ra khoảng biến thiên R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.

+ Q₁ và Q₃ tăng 2 đơn vị nên khoảng tứ phân vị Δ_Q = Q₃ − Q₁ không đổi vì phần tăng thêm bị triệt tiêu cho nhau.

+ Giá trị trung bình tăng 2 đơn vị

Nên độ lệch của mỗi giá trị so với giá trị trung bình $|x_i-\overline{x}|$ không đổi vì phần tăng thêm bị triệt tiêu cho nhau.

Suy ra ${(x_i-\overline{x})}^2$ không đổi

Khi đó, phương sai không đổi.

Do đó độ lệch chuẩn không đổi.

Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

Bài 5.14 trang 88 Toán 10 Tập 1: Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:

Giá trị nhỏ nhất bằng 2,5; Q₁ = 36; Q₂ = 60; Q₃ = 100; giá trị lớn nhất bằng 205.

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?

b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.

c) Tìm khoảng tứ phân vị của mẫu số liệu.

Lời giải:

a) Vì số các giá trị của số liệu n = 51 là số lẻ nên trung vị của số liệu là giá trị thứ 26.

Nửa bên trái số trung vị gồm 25 số liệu là số lẻ nên tứ phân vị thứ nhất là giá trị thứ 13 có giá trị là 36.

Do đó có 51 – 13 = 38 thành phố có thuế thuốc lá lớn hơn 36.

Suy ra tỉ lệ các thành phố có thuế thuốc lá lớn hơn 36 là: $\frac{38}{51}\approx 74,51\%.$

Vậy tỉ lệ các thành phố có thuế thuốc là lớn hơn 36 khoảng 74,51%.

b)

Có nhiều phương án để lựa chọn trong bài này.

Chẳng hạn ta chọn hai giá trị là Q₁ và Q₃, vì khoảng giữa hai giá trị này là khoảng tứ phân vị và khoảng này là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.

Vậy giữa hai giá trị Q₁ = 36 và Q₃ = 100 có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này. 

c) Khoảng tứ phân vị của mẫu số liệu này là:

∆_Q = Q₃ – Q₁ = 100 – 36 = 64.

Bài 5.15 trang 88 Toán 10 Tập 1: Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):

2,977          3,155          3,920          3,412          4,236

2,593          3,270          3,813          4,042          3,387.

Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.

Lời giải

Sắp xếp các giá trị của số liệu trên theo thứ tự từ không giảm là:

2,593; 2,977; 3,155; 3,270; 3,387; 3,412; 3,813; 3,920; 4,042; 4,236.

Ta có giá trị lớn nhất là 4,236 kg và giá trị nhỏ nhất là 2,593 kg.

Khi đó, khoảng biến thiên là: R = 4,236 – 2,593 = 1,643.

Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa:

Q₂ = (3,387 + 3,412) : 2 = 3,3995.

Nửa số liệu bên trái gồm 5 số liệu là một số lẻ nên tứ phân vị thứ nhất là: Q₁ = 3,155.

Nửa số liệu bên phải gồm 5 số liệu là một số lẻ nên tứ phân vị thứ ba là: Q₃ = 3,920.

Khoảng tứ phân vị là: ∆_Q = Q₃ – Q₁ = 3,920 – 3,155 = 0,765.

Số trung bình cộng của mẫu số liệu là:

$\overline{X}=\frac{2,593+2,977+3,155+3,270+3,387+3,412+3,813+3,920+4,042+4,236}{10}$

$=3,4805$

Ta có bảng sau:

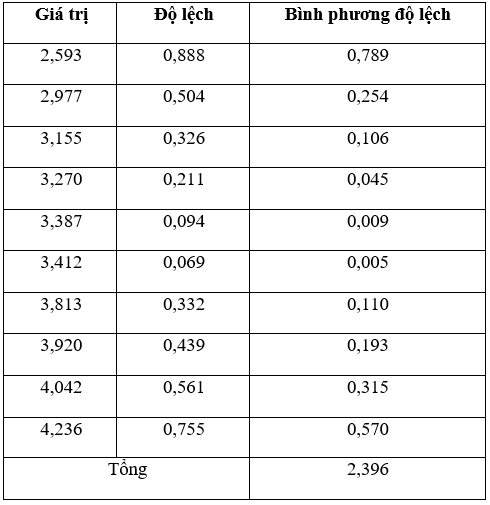
Phương sai: $s^2\approx \frac{2,396}{10}=0,2396$

Độ lệch chuẩn: $s=\sqrt{s^2}\approx \sqrt{0,2396}\approx 0,489$.

Vậy khoảng biến thiên R = 1,643, khoảng tứ phân vị ${\Delta }_Q=0,765;$ độ lệch chuẩn s ≈ 0,489.

Bài 5.16 trang 88 Toán 10 Tập 1: Tỉ lệ thất nghiệp ở một quốc gia vào năm 2007 (đơn vị %) được cho như sau:

7,8     3,2     7,7     8,7     8,6     8,4     7,2     3,6

5,0     4,4     6,7     7,0     4,5     6,0     5,4.

Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.

Lời giải:

Sắp xếp dãy số liệu theo thứ tự không giảm, ta được:

3,2; 3,6; 4,4; 4,5; 5,0; 5,4; 6,0; 6,7; 7,0; 7,2; 7,7; 7,8; 8,4; 8,6; 8,7.

Vì n = 15 là số lẻ nên số trung vị là giá trị chính giữa Q₂ = 6,7.

Nửa số liệu bên trái có 7 số liệu nên có tứ phân vị thứ nhất là Q₁ = 4,5.

Nửa số liệu bên phải có 7 số liệu nên có tứ phân vị thứ ba là Q₃ = 7,8.

Khoảng tứ phân vị là: ∆_Q = Q₃ – Q₁ = 7,8 – 4,5 = 3,3.

Ta có:

Q₁ – 1,5Δ_Q = 4,5 – 4,95 = – 0,45;

 Q₃ + 1,5Δ_Q = 7,8 + 4,95 = 12,75.

Ta thấy không có giá trị nào dưới –0,45 và trên 12,75 nên không có giá trị bất thường.

Vậy mẫu số liệu đã cho không có giá trị nào bất thường.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Giải Toán 10 trang 84 Tập 1

Giải Toán 10 trang 85 Tập 1

Giải Toán 10 trang 86 Tập 1

Giải Toán 10 trang 87 Tập 1