Nội dung bài viết

    Xem thêm

    Giải SBT Toán 7 trang 9 Tập 1 Cánh diều

    Với Giải SBT Toán 7 trang 9 Tập 1 trong Bài 1: Tập hợp Q các số hữu tỉ Toán lớp 7 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 9.

    1 2,090 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 trang 9 Tập 1 Cánh diều

    Bài 1 trang 9 SBT Toán 7 Tập 1: Các số 0,5; 11; 3,111 457; −34; −1,3; −1−3;  −98 có là số hữu tỉ không? Vì sao?

    Lời giải:

    Ta có 

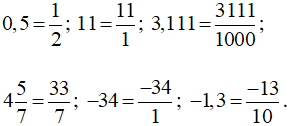
    Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1)

    Vì các số 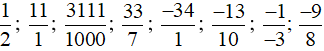Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1) có dạng ab, với a, b Î ℤ, b ≠ 0.

    Nên các số Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1) là số hữu tỉ.

    Vậy các số 0,5; 11; 3,111 457; −34; −1,3; −1−3;  −98 là số hữu tỉ.

    Bài 2 trang 9 SBT Toán 7 Tập 1: Chọn kí hiệu "Î", "Ï" thích hợp cho   ?  .

    a) −13    ?    ℕ;                 b) −345  987    ?    ℤ;                  c) 0    ?    ℚ;

    d) 103475     ?    ℚ;              e) 301756     ?    ℤ;                          g) 13−499    ?    ℚ;

    h) −11,01     ?    ℤ             i) −21−128     ?    ℚ;                        k) 0,3274    ?    ℚ

    Lời giải:

    ∙ Vì −13 là số nguyên âm nên −13 không thuộc tập hợp số tự nhiên.

    Do đó −13    ∉    ℕ;

    ∙ Vì −345 987 là số nguyên âm nên −345 987 thuộc tập hợp số nguyên.

    Do đó −345  987    ∈    ℤ;

    ∙ Ta có: 0=01. Vì 0; 1 Î ℤ; 1 ≠ 0 nên 01 là số hữu tỉ hay 0 thuộc tập hợp ℚ.

    Do đó 0     ∈    ℚ;

    ∙ Ta có: 103475=78475. Vì 784; 75 Î ℤ; 75 ≠ 0 nên 78475 là số hữu tỉ hay 103475 thuộc tập hợp ℚ.

    Do đó 103475     ∈    ℚ;

    ∙ Vì 301⋮756 nên 301756 không thuộc tập hợp số nguyên.

    Do đó 301756     ∉    ℤ;

    ∙ Vì 13; −499 Î ℤ; −499 ≠ 0 nên 13−499 là số hữu tỉ hay 13−499 thuộc tập hợp ℚ.

    Do đó 13−499    ?    ℚ;

    ∙ Số −11,01 không phải là số nguyên nên −11,01     ∈    ℤ

    ∙ Vì −21; −128 Î ℤ; −128 ≠ 0 nên −21−128 là số hữu tỉ hay −21−128 thuộc tập hợp ℚ.

    Do đó −21−128     ∈    ℚ

    ∙ Ta có: 0,3274=3  27410  000. Vì 3 274; 10 000 Î ℤ; 10 000 ≠ 0 nên 3  27410  000 là số hữu tỉ hay 0,3274 thuộc tập hợp ℚ.

    Do đó 0,3274    ∈    ℚ

    Vậy ta điền vào ô trống như sau:

    a) −13    ∉    ℕ;                b) −345  987    ∈    ℤ;                  c) 0    ∈    ℚ;

    d) 103475     ∈    ℚ;             e) 301756     ∉    ℤ;                         g) 13−499    ∈    ℚ;

    h) −11,01     ∉    ℤ            i) −21−128     ∈    ℚ;                       k) 0,3274    ∈    ℚ

    Bài 3 trang 9 SBT Toán 7 Tập 1: Trong giờ học nhóm, ba bạn An, Bình, Chi lần lượt phát biểu như sau:

    - An: "Số 0 là số nguyên và không phải là số hữu tỉ."

    - Bình: "Số hữu tỉ là số viết được dưới dạng phân số 01 với a, b Î ℤ."

    - Chi: "Mỗi số nguyên là một số hữu tỉ."

    Theo em, bạn nào phát biểu đúng, bạn nào phát biểu sai? Vì sao?

    Lời giải:

    - An phát biểu sai do 0 viết được dưới dạng phân số ab nên 0 là số hữu tỉ.

    - Bình phát biểu sai do số hữu tỉ là số viết được dưới dạng phân số ab với a, b Î ℤ, b ≠ 0.

    - Chi phát biểu đúng do mỗi số nguyên a viết được dưới dạng phân số .

    Bài 4 trang 9 SBT Toán 7 Tập 1: Quan sát trục số ở Hình 5, điểm nào biểu diễn số hữu tỉ 34?

    Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1)

    Lời giải:

    a)

    Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1)

    Ta thấy: 34 là số hữu tỉ dương và 0<34<1.

    Ta chia đoạn thẳng đơn vị thành 4 phần bằng nhau, lấy một đoạn làm đơn vị mới.

    Khi đó, điểm biểu diễn số hữu tỉ 34 là điểm nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 3 lần đơn vị mới.

    Do đó điểm C biểu diễn số hữu tỉ 34.

    Vậy trên trục số ở Hình 5, điểm C biểu diễn số hữu tỉ 34.

    Bài 5 trang 9 SBT Toán 7 Tập 1: Tìm số đối của mỗi số hữu tỉ sau: 37221; −931171; 87−19  543; 41,02; −791,8.

    Lời giải:

    Số đối của 37221 là −37221;

    Số đối của −931171 là −−931171=931171;

    Số đối của 87−19  543 là −87−19  543=8719  543;

    Số đối của 41,02 là −41,02;

    Số đối của −791,8 là 791,8.

    Vậy số đối của các số 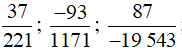Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1); 41,02; −791,8 lần lượt là Sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ - Cánh diều (ảnh 1); −41,02; 791,8.

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

    Giải SBT Toán 7 trang 10 Tập 1

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,090 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: