Nội dung bài viết

    Xem thêm

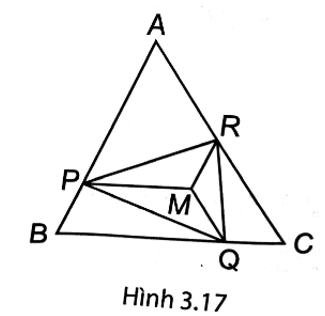
    Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB

    Lời giải Bài 4 trang 50 vở thực hành Toán 8 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Vở thực hành Toán 8.

    1 5,124 28/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Vở thực hành Toán 8 Luyện tập chung trang 49

    Bài 4 trang 50 vở thực hành Toán 8 Tập 1: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

    a) Chứng minh tứ giác APMR là hình thang cân.

    b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

    c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều.

    Lời giải:

    Cho M là một điểm nằm trong tam giác đều ABC

    (H.3.17). a) Do MR // AP nên tứ giác APMR là hình thang.

    Ta có A^=60° (do ∆ABC đều).

    Do MP // BC nên B^=APM^=60°. Từ đó suy ra A^=APM^ nên APMR là hình thang cân.

    b) Tương tự câu a, ta có các tứ giác BQMP và CRMQ là những hình thang cân.

    Do APMR, BQMP và CRMQ là những hình thang cân, suy ra RP = AM, PQ = BM, QR = CM (hai đường chéo của hình thang cân).

    Chu vi của tam giác PQR là

    PQ + RP + QR = BM + AM + CM.

    c) Tam giác PQR là tam giác đều có nghĩa là PQ = QR = RP, tức là MB = MC = MA.

    Vậy M cách đều ba đỉnh A, B, C tức M là giao điểm của ba đường trung trực của tam giác ABC.

    *Phương pháp giải

    *Lý thuyết:

    1. Đường trung trực của tam giác

    – Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.

    Chú ý: Đường trung trực của một tam giác có thể không đi qua đỉnh nào của tam giác.

    2. Tính chất ba đường trung trực của tam giác

    – Ba đường trung trực của một tam giác cùng đi qua một điểm.

    Nhận xét:

    + Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.

    + Giao điểm ba đường trung trực của một tam giác cách đều ba đỉnh của tam giác đó.

    Do đó, trong một tam giác ba đường trung trực cùng đi qua một điểm và điểm đó cách đều ba đỉnh của tam giác.

    Xem thêm

    Lý thuyết Tính chất ba đường trung trực của tam giác – Toán 7 Cánh diều

    TOP 15 câu Trắc nghiệm Tính chất ba đường trung trực của tam giác (Chân trời sáng tạo 2024) có đáp án - Toán 7

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 1 trang 49 vở thực hành Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.14 có phải là hình thang không? Vì sao...

    Bài 2 trang 50 vở thực hành Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết ABD^=30°, tính số đo góc của hình thang đó...

    Bài 3 trang 50 vở thực hành Toán 8 Tập 1: Tính số đo các góc của tứ giác ABCD trong Hình 3.16...

    Bài 4 trang 50 vở thực hành Toán 8 Tập 1: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA...

    Bài 5 trang 51 vở thực hành Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN...

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 10: Tứ giác

    Bài 12: Hình bình hành

    Luyện tập chung trang 54

    Bài 13: Hình chữ nhật

    Bài 14: Hình thoi và hình vuông

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 5,124 28/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: