Bài 3 trang 87 Toán 8 Tập 1 | Chân trời sáng tạo Giải Toán 8

Lời giải Bài 3 trang 87 Toán 8 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 Tập 1.

1 415 24/04/2023

Trang trước

Trang sau

Giải Toán 8 Bài 5: Hình chữ nhật – Hình vuông

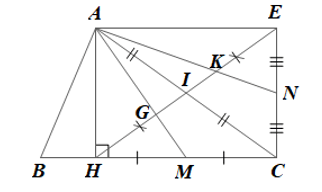
Bài 3 trang 87 Toán 8 Tập 1: Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Lời giải:

Bài 3 trang 87 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) Do E là điểm đối xứng với H qua I nên I là trung điểm của HE.

Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên là hình bình hành.

Lại có $\hat{A H C} = 90 °$ nên hình bình hành AHCE là hình chữ nhật.

b) Xét DAHC có AM, HI là hai đường trung tuyến cắt nhau tại G nên G là trọng tâm của DAHC.

Suy ra $H G = \frac{2}{3} H I$ và $I G = \frac{1}{2} H G$ .

Chứng minh tương tự đối với DAEC có K là trọng tâm của DAEC.

Suy ra $E K = \frac{2}{3} E I$ và $I K = \frac{1}{2} E K$ .

Ta có: $H G = \frac{2}{3} H I$ , $E K = \frac{2}{3} E I$ và HI = EI nên $H G = E K (= \frac{2}{3} E I)$ .

Lại có: $I G = \frac{1}{2} H G$ và $I K = \frac{1}{2} E K$ nên $I G = I K = \frac{1}{2} H G$

Mặt khác $G K = I G + I K = \frac{1}{2} H G + \frac{1}{2} H G = H G$ .

Vậy HG = GK = KE.

Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 82 Toán 8 Tập 1: Mỗi viên gạch trong hình bức tường có bề mặt hình chữ nhật được minh hoạ bởi hình bên...

Khám phá 1 trang 82 Toán 8 Tập 1: Dùng thước đo góc để đo số đo các góc ở Hình 1 và rút ra nhận xét về số đo của chúng...

Khám phá 2 trang 82 Toán 8 Tập 1: Cho ABCD là hình chữ nhật. a) Chứng minh AB // CD và AD // BC...

Thực hành 1 trang 83 Toán 8 Tập 1: Cho biết a, b, d lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp...

Vận dụng 1 trang 83 Toán 8 Tập 1: Tìm bốn ví dụ về hình chữ nhật trong thực tế...

Khám phá 3 trang 83 Toán 8 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau...

Thực hành 2 trang 84 Toán 8 Tập 1: Chỉ được sử dụng compa, hãy kiểm tra tứ giác ở Hình 6 có phải là hình chữ nhật hay không...

Vận dụng 2 trang 84 Toán 8 Tập 1: a) Hãy sử dụng êke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không...

Khám phá 4 trang 84 Toán 8 Tập 1: Cho tứ giác ABCD có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ ABCD vừa là hình thoi vừa là hình chữ nhật...

Khám phá 5 trang 85 Toán 8 Tập 1: Cho hình vuông MNPQ. Chứng minh MNPQ vừa là hình chữ nhật vừa là hình thoi...

Thực hành 3 trang 85 Toán 8 Tập 1: Tìm hình vuông trong hai hình sau...

Vận dụng 3 trang 85 Toán 8 Tập 1: Tìm bốn ví dụ về hình vuông trong thực tế...

Khám phá 6 trang 85 Toán 8 Tập 1: Cho hình chữ nhật ABCD. Giải thích tại sao ABCD là hình vuông trong mỗi trường hợp sau...

Khám phá 7 trang 86 Toán 8 Tập 1: Cho hình thoi ABCD. Hãy chứng tỏ: a) Nếu $\hat{B A D}$ là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông...

Thực hành 4 trang 86 Toán 8 Tập 1: Trong Hình 12, cho biết ABCD là một hình vuông. Chứng minh rằng...

Vận dụng 4 trang 86 Toán 8 Tập 1: Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13)...

Bài 1 trang 87 Toán 8 Tập 1: Cho Hình 14. Tìm x...

Bài 2 trang 87 Toán 8 Tập 1: Cho Hình 15. Vẽ thêm điểm P để tứ giác MNPQ là hình chữ nhật...

Bài 3 trang 87 Toán 8 Tập 1: Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I...

Bài 4 trang 87 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB)...

Bài 5 trang 87 Toán 8 Tập 1: Lấy một tờ giấy, gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON...

Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3

1 415 24/04/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: