Toán 9 Bài 2 (Chân trời sáng tạo): Căn bậc ba

Với giải bài tập Toán lớp 9 Bài 2: Căn bậc ba sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9 Bài 2.

1 580 03/04/2024
Trang trước
Trang sau  

Giải Toán 9 Bài 2: Căn bậc ba

Hoạt động khám phá 1 trang 42 Toán 9 Tập 1: Có hai khối bê tông hình lập phương A và B có thể tích lần lượt là 8 dm3 và 15 dm3 (Hình 1).

Giải SGK Toán 9 Bài 2 (Chân trời sáng tạo): Căn bậc ba (ảnh 1)

a) Tính độ dài cạnh của khối bê tông A.

b) Gọi x (dm) là độ dài cạnh của khối bê tông B. Thay ? bằng số thích hợp để có đẳng thức: x3 = ?

Lời giải:

a) Độ dài cạnh của khối bê tông A là: 3√V=3√8=2 dm

b) VB = x3 = 15.

Thực hành 1 trang 43 Toán 9 Tập 1: Tìm căn bậc ba của mỗi số sau:

a) -1

b) 64

c) – 0,064

d) 127

Lời giải:

a) Ta có (-1)3 = 1, suy ra 3√−1 = - 1

b) Ta có 43 = 64, suy ra 3√64=4

c) Ta có (-0,4)3 = - 0,064, suy ra 3√−0,064=−0,4

d) Ta có (13)3=127, suy ra 3√127=13.

Thực hành 2 trang 43 Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) A = 3√8000+3√0,125

b) B = 3√123−3√(−11)3

c) C = (3√4)3+(3√−5)3

Lời giải:

a) A = 3√8000+3√0,125

=3√(20)3+3√(0,5)3=20+0,5=20,5

b) B = 3√123−3√(−11)3

3√123−3√(−11)3=12−(−11)=23

c) C = (3√4)3+(3√−5)3

(3√4)3+(3√−5)3=4−5=−1

Thực hành 3 trang 44 Toán 9 Tập 1: Sử dụng máy tính cầm tay, tìm căn bậc ba của các số sau (kết quả làm tròn dến chữ số thập phân thứ ba):

a) 25

b) -100

c) 8,5

d) 15

Lời giải:

a) 3√25≈2,924

b) 3√−100≈−4,642

c) 3√8,5≈2,041

d) 3√15≈0,585

Vận dụng trang 44 Toán 9 Tập 1: Đối với bài toán phần khởi động (trang 42): Một bể cá hình lập phương có sức chứa 1000 dm3 . Muốn tăng sức chứa của bể lên 10 lần (giữ nguyên hình dạng lập phương) thì phải tăng chiều dài mỗi cạnh lên bao nhiêu lần?

Lời giải:

Gọi độ dài cạnh của hình lập phương sau khi tăng là x (dm)

Ta có V = x3 mà muốn tăng sức chứa của bể lên 10 lần thì:

x = 3√10.V=3√10.1000=3√10.10dm

Vậy phải tăng mỗi cạnh lên 3√10 dm.

Hoạt động khám phá 2 trang 44 Toán 9 Tập 1: Ông An có một bể kính hình lập phương như Hình 2.

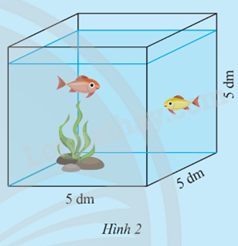
Giải SGK Toán 9 Bài 2 (Chân trời sáng tạo): Căn bậc ba (ảnh 2)

Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính).

a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức:

a3 = ? hay a = ?.

b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).

Lời giải:

a) a3 = (5.5.5).n = 125n hay a = 3√125n=53√n.

b) Khi n = 8, ta được: a = 53√n=53√8=5.2=10

Khi n = 4, ta được: a = 53√n=53√4≈7,94.

Thực hành 4 trang 44 Toán 9 Tập 1: Cho biểu thức Q = 3√3x2. Tính giá trị của Q khi x = 2 và khi x = - 3 (kết quả làm tròn đến chữ số thập phân thứ hai).

Lời giải:

Khi x = 2 suy ra Q = 3√3.22≈2,29.

Khi x = - 3 suy ra Q = 3√3.(−3)2=3.

Bài tập

Bài 1 trang 45 Toán 9 Tập 1: Tìm căn bậc ba của mỗi số sau:

a) -64

b) 27000

c) – 0,125

d) 338

Lời giải:

a) Ta có (-4)3 = -64, suy ra 3√−64=−4

b) Ta có 303 = 27000, suy ra 3√27000=30

c) Ta có (-0,5)3 = -0,125, suy ra 3√−0,125=−0,5

d) Ta có 338=278 mà (32)3=278, suy ra 3√278=32 .

Bài 2 trang 45 Toán 9 Tập 1: Tính

a) 3√0,001

b) 3√−164

c) −3√113

d) (3√−216)3

Lời giải:

a) 3√(0,1)3=0,1

b) 3√(−14)3=−14

c) −3√113=−11

d) (3√−216)3=−216.

Bài 3 trang 45 Toán 9 Tập 1: Hoàn thành bảng sau vào vở:

Giải SGK Toán 9 Bài 2 (Chân trời sáng tạo): Căn bậc ba (ảnh 3)

Lời giải:

Giải SGK Toán 9 Bài 2 (Chân trời sáng tạo): Căn bậc ba (ảnh 4)

Bài 4 trang 45 Toán 9 Tập 1: Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ ba):

a) 3√79

b) 3√−6,32

c) 3√19+3√202

Lời giải:

a) 3√79≈4,291

b) 3√−6,32≈−1,849

c) 3√19+3√202≈2,691

Bài 5 trang 45 Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) A = 3√83+(3√−7)3

b) B = 3√1000000−3√0,027

Lời giải:

a) A = 3√83+(3√−7)3=8−7=1

b) B = 3√1000000−3√0,027=100−0,3=99,7

Bài 6 trang 45 Toán 9 Tập 1: Tìm x, biết:

a) x3 = - 27

b) x3 = 64125

c) 3√x=8

d) 3√x=−0,9

Lời giải:

a) x3 = - 27

x = 3√−27=−3

b) x3 = 64125

x = 3√64125=45

c) 3√x=8

x = 83 = 512

d) 3√x=−0,9

x = (-0,9)3 = - 0,729

Bài 7 trang 45 Toán 9 Tập 1: Tính giá trị của biểu thức P = 3√64n khi n = 1; n = - 1; n = 1125.

Lời giải:

Khi n = 1 ta có: P = 3√64.1=4

Khi n = - 1 ta có: P = 3√64.(−1)=3√−64=−4

Khi n = 1125 ta có: P = 3√64.(1125)=3√(45)3=45

Bài 8 trang 45 Toán 9 Tập 1: Một khối hình lập phương có thể tích 1000 cm3. Chia khối gỗ này thành 8 khối gỗ hình lập phương nhỏ có thể tích bằng nhau. Tính độ dài cạnh của mỗi khối gỗ hình lập phương nhỏ.

Lời giải:

Thể tích 1 khối gỗ hình lập phương nhỏ là V8=10008=125( cm3)

Độ dài cạnh của mỗi khối gỗ hình lập phương nhỏ là: 3√125=5 (cm).

Tham khảo các loạt bài Toán 9 khác:

Bài viết cùng lớp mới nhất

Xem thêm
1 580 03/04/2024
Trang trước
Trang sau  

Xem thêm các chương trình khác: