Giải Toán 9 Bài 3 (Chân trời sáng tạo): Hình cầu

Giải bài tập Toán 9 Bài 3: Hình cầu

Khởi động trang 93 Toán 9 Tập 2: Các vật thể quen thuộc ở hình bên có đặc điểm gì chung? Hãy kể tên một vài vật thể có hình dạng tương tự.

Lời giải:

Các vật này có đặc điểm chung là có một tâm và khi cắt các vật này bằng một mặt phẳng thì sẽ được một hình tròn.

Một vài vật thể trong thực tế có dạng tương tự là: quả dưa hấu, quả bóng đá, viên bi,...

1. Hình cầu

Khám phá 1 trang 93 Toán 9 Tập 2: Cho tấm bìa có dạng nửa hình tròn tâm O và đường kính AB cố định (Hình 1a). Quay tấm bìa quanh đường kính AB thì hình tạo ra giống với vật thể quen thuộc nào?

Lời giải:

Quay tấm bìa quanh đường kính AB thì hình tạo ra giống với quả địa cầu, quả bóng, viên bi,...

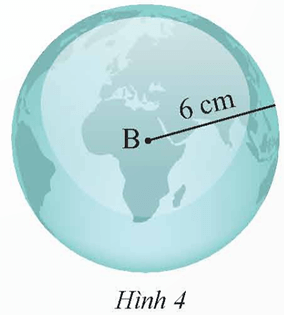
Thực hành 1 trang 94 Toán 9 Tập 2: Quả địa cầu bằng pha lê ở Hình 4 có dạng hình cầu. Quan sát và cho biết tâm và bán kính của hình quả địa cầu đó.

Lời giải:

Quan sát quả địa cầu bằng pha lê ở Hình 4 có dạng hình cầu, ta thấy:

• Tâm của hình địa cầu là B.

• Bán kính hình địa cầu là 6 cm.

Khám phá 2 trang 94 Toán 9 Tập 2: Quan sát Hình 5 và cho biết mặt cắt quả cam có dạng hình gì.

Lời giải:

Quan sát Hình 5, ta thấy mặt cắt của quả cam có dạng hình tròn.

Thực hành 2 trang 94 Toán 9 Tập 2: Mặt trên của bình gốm (Hình 8) được xem là phần chung của mặt phẳng và mặt cầu. Mặt trên của bình gốm dạng gì?

Lời giải:

Quan sát Hình 5, ta thấy mặt trên của bình gốm có dạng đường tròn.

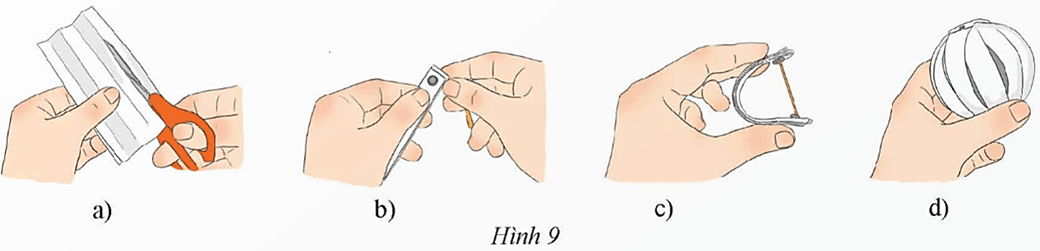
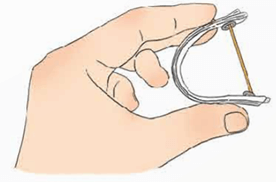
Vận dụng 1 trang 95 Toán 9 Tập 2: Gấp chiếc đèn trang trí dạng hình cầu (mặt cầu) theo hướng dẫn sau:

− Cắt các mảnh giấy hình chữ nhật có chiều dài 20 cm, chiều rộng 1 cm (Hình 9a).

− Đục lỗ rồi dùng nút gắn vào nhau (Hình 9b).

− Cố định hai lỗ bằng que tre có độ dài bằng $\frac{2x}{\pi }$ (khoảng 0,6x) với x là khoảng cách giữa hai cái lỗ (Hình 9c).

− Tách các mảnh giấy ra và trải đều, hình được tạo thành có dạng hình cầu (Hình 9d).

Lời giải:

HS thực hành theo các bước như trong Hình 9 như sau:

Bước 1: Cắt các mảnh giấy hình chữ nhật có chiều dài 20 cm, chiều rộng 1 cm.

Bước 2: Đục lỗ rồi dùng nút gắn vào nhau.

Bước 3: Cố định hai lỗ bằng que tre có độ dài bằng $\frac{2x}{\pi }$ (khoảng 0,6x) với x là khoảng cách giữa hai cái lỗ.

Bước 4: Tách các mảnh giấy ra và trải đều, hình được tạo thành có dạng hình cầu.

2. Diện tích của mặt cầu

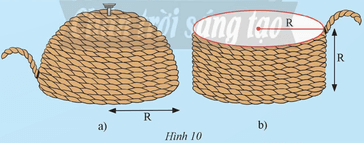
Khám phá 3 trang 95 Toán 9 Tập 2: Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.

a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.

b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.

Lời giải:

a) Diện tích xung quanh của phần hình trụ là: S = 2πR . R = 2πR².

Vậy diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b là 2πR².

b) Theo đề bài, chiều cao của phần hình trụ được quấn dây bằng bán kính R.

Dự đoán: Diện tích nửa mặt cầu là 2πR².

Vận dụng 2 trang 96 Toán 9 Tập 2: Tìm diện tích bề mặt của Mặt Trăng, biết đường kính Mặt Trăng là khoảng 3 474 km.

Lời giải:

Bán kính Mặt Trăng là: $R=\frac{3474}{2}=1737\left(km\right).$

Diện tích bề mặt của Mặt Trăng là:

S = 4πR² = 4π. (1 737)² ≈ 37 914 864 (km²).

Vậy diện tích bề mặt của Mặt Trăng khoảng 37 914 864 km².

3. Thể tích của hình cầu

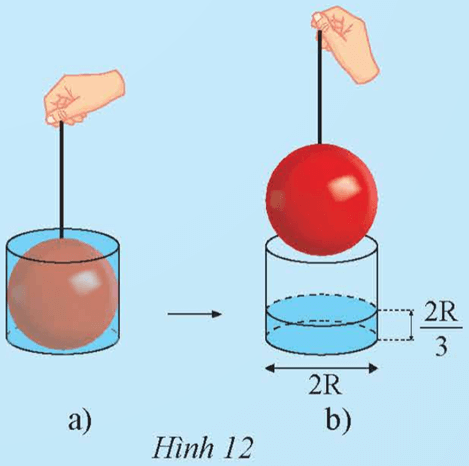
Khám phá 4 trang 96 Toán 9 Tập 2: Một quả cầu có bán kính R nằm khít trong chiếc bình hình trụ đổ đầy nước có chiều cao h = 2R (Hình 12a). Rút qua cầu ra khỏi bình nước, ta thấy chiều cao của mực nước bằng $\frac{1}{3}$ chiều cao h (Hình 12b). Hãy tính theo R:

a) Thể tích của chiếc bình hình trụ;

b) Thể tích của nước ở trong bình;

c) Thể tích của hình cầu.

Lời giải:

a) Thể tích của chiếc bình hình trụ V₁ = πR² . 2R = 2πR³.

b) Thể tích của nước ở trong bình là:

$V_2=\pi \cdot R^2\cdot \frac{2R}{3}=\frac{2\pi R^3}{3}.$

c) Thể tích của hình cầu là:

$V=V_1-V_2=2\pi R^3-\frac{2\pi R^3}{3}=\frac{4\pi R^3}{3}.$

Vậy thể tích của hình cầu là $\frac{4\pi R^3}{3}.$

Thực hành 3 trang 96 Toán 9 Tập 2: Một quả bóng rổ (khi bơm căng) có đường kính 24 cm (Hình 14). Tìm thể tích của quả bóng rổ đó (kết quả làm tròn đến hàng đơn vị).

Lời giải:

Bán kính quả bóng rổ khi bơm căng là: R = $\frac{24}{2}$ = 12 (cm).

Thể tích của quả bóng rổ là:

$V=\frac{4}{3}\pi R^3=\frac{4}{3}\cdot \pi \cdot {12}^3\approx 7238\left(c{m}^3\right).$

Vậy thể tích của quả bóng rổ đó khoảng 7 238 cm³.

Bài tập

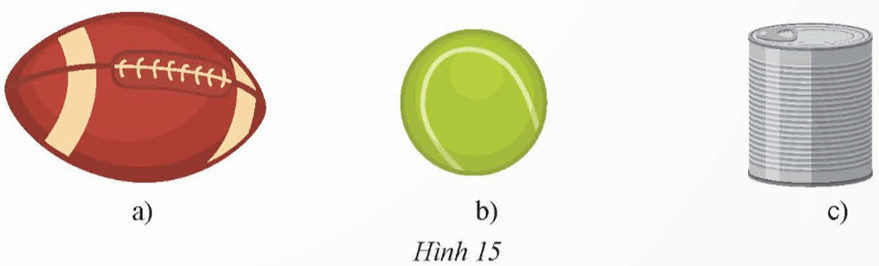
Bài 1 trang 96 Toán 9 Tập 2: Đồ vật nào sau đây có dạng hình cầu?

Lời giải:

Quan sát Hình 15, ta thấy:

• Hình 15a) không phải là hình cầu;

• Hình 15b) là hình cầu;

• Hình 15c) là hình trụ.

Vậy quả bóng ở Hình 15b) có dạng hình cầu.

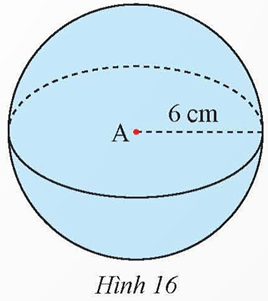
Bài 2 trang 97 Toán 9 Tập 2: Quan sát hình cầu ở Hình 16. Hãy cho biết tâm, bán kính, diện tích mặt cầu và thể tích của hình cầu đó.

Lời giải:

Mặt cầu ở Hình 16 có tâm là A, bán kính là 6 cm.

Diện tích mặt cầu là: 4 . π . 6² = 144π (cm²).

Thể tích hình cầu là: $\frac{4}{3}\cdot \pi \cdot 6^3=288\pi \left(c{m}^3\right).$

Bài 3 trang 97 Toán 9 Tập 2: Bể cá ở Hình 17 là một phần của một hình cầu. Hỏi mặt nước trong bể cá có dạng hình gì?

Lời giải:

Mặt nước trong bể cá ở Hình 17 có dạng hình tròn.

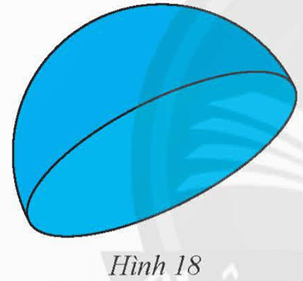
Bài 4 trang 97 Toán 9 Tập 2: Cắt một hình cầu có bán kính 5 cm bằng một mặt phẳng đi qua tâm ta sẽ được hai nửa hình cầu. Nam cầu sơn tất cả các mặt của một nửa hình cầu này (Hình 18). Hỏi diện tích Nam cần sơn là bao nhiêu (kết quả làm tròn đến hàng đơn vị)?

Lời giải:

Diện tích Nam cần sơn gồm diện tích xung quanh nửa mặt cầu và diện tích mặt cắt.

Khi đó, diện tích Nam cần sơn là:

S = π . 5² + 2π . 5² = 75π ≈ 236 (cm²).

Vậy diện tích Nam cần sơn khoảng 236 cm².

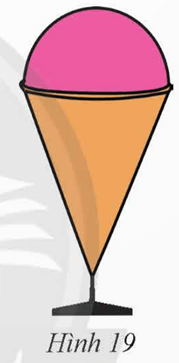
Bài 5 trang 97 Toán 9 Tập 2: Phần bên trong của một cái li có dạng hình nón có bán kính đáy 2 cm, độ dài đường sinh 8 cm. Người ta đựng đầy kem trong li và thêm một nửa hình cầu kem phía trên (Hình 19). Tính thể tích của kem (kết quả làm tròn đến hàng đơn vị).

Lời giải:

Trong Hình 19, bán kính đáy của hình nón cũng là bán kính nửa mặt cầu và bằng 2 cm.

Chiều cao hình nón là: $\sqrt{8^2-2^2}=2\sqrt{15}\left(cm\right).$

Thể tích hình nón là:

$V_1=\frac{1}{3}\cdot \pi \cdot 2^2\cdot 2\sqrt{15}=\frac{8\sqrt{15}}{3}\pi \left(c{m}^3\right).$

Thể tích của nửa hình cầu là:

$V_2=\frac{1}{2}\cdot \frac{4}{3}\cdot \pi \cdot 2^3=\frac{16}{3}\pi \left(c{m}^3\right).$

Thể tích của kem là:

$V=V_1+V_2=\frac{8\sqrt{15}}{3}\pi +\frac{16}{3}\pi \approx 49\left(c{m}^3\right).$

Vậy thể tích của kem khoảng 49 cm³.

Xem thêm Lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hình nón

Bài tập cuối chương 10

Hoạt động 3: Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0) bằng phần mềm GeoGebra

Hoạt động 4: Chuyển dữ liệu từ bảng vào biểu đồ trên phần mềm Microsoft Word

Hoạt động 5: Cắt đa giác đều làm vòng quay may mắn